3.3. Задача Коши. Общие замечания
Задача Коши является одной из основных задач теории дифференциальных уравнений и заключается в отыскании решения (интеграла) дифференциального уравнения, удовлетворяющего начальным данным (начальным условиям). В задаче Коши область, в которой должно быть определено решение, заранее не указывается.
Так как задача Коши
возникает при анализе процессов,
определяемых дифференциальным законом
и начальным состоянием, математическим
выражением которых является уравнение
и начальное условие (откуда терминология
и выбор обозначений: начальные данные
задаются при x
= 0, а решение
отыскивается при
),
то если x
интерпретировать как время, а
как обобщенные координаты некоторой
механической системы, то получим
следующий аспект задачи Коши: зная
дифференциальные уравнения, управляющие
механической системой, а также состояние
ее в начальный момент времени
,
определить
состояние системы в любой момент времени
х.
Простейшим обыкновенным дифференциальным уравнением [12] является уравнение первого порядка
.
(3.4)
Основная задача, относящаяся к этому уравнению, есть задача Коши: найти решение уравнения (3.4)
,
(3.5)
удовлетворяющее
начальному
условию
(иными словами, требуется найти
интегральную кривую
,
проходящую через заданную точку
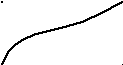
(рис. 5)).
y
y
0
x
x
Рис. 5
В приложениях часто встречаются системы обыкновенных дифференциальных уравнений. Ограничимся рассмотрением нормальной системы n-го порядка обыкновенных дифференциальных уравнений (т.е. система разрешена относительно производных):
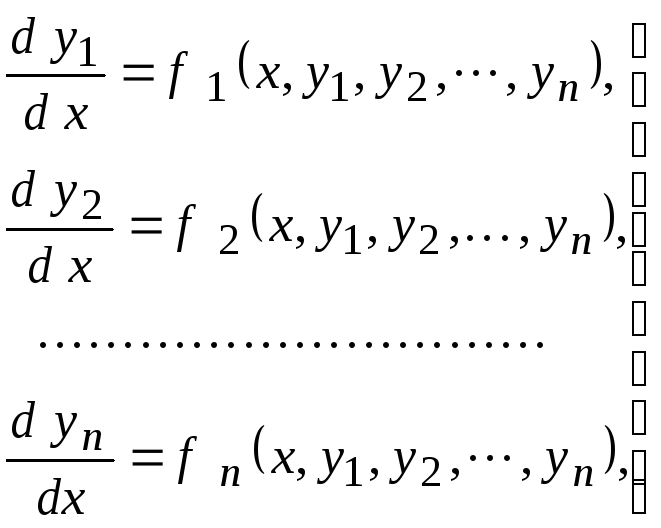(3.8)
где x
независимая переменная,
искомые функции.
Заметим, что систему, содержащую производные высших порядков и разрешенных относительно старших производных искомых функций, путем введения неизвестных функций можно привести к виду (3.8). В частности, для дифференциального уравнения n-го порядка
,
(3.9)
полагая
,
будем иметь эквивалентную нормальную
систему
(3.10)
Так как система
дифференциальных уравнений имеет
бесчисленное множество решений, то для
выделения одного конкретного решения
,
кроме уравнения, нужны дополнительные
условия.
В простейшем случае задаются начальные условия
,
(3.13)
что приводит к задаче Коши.
3.4. Метод Пикара
Знакомство с численными методами решения обыкновенных дифференциальных уравнений начнем с метода Пикара (или метода последовательных приближений, или последовательной подстановки). Решение в методе Пикара получается в виде аналитического выражения, т.е. как зависимость функции от непрерывно изменяющихся значений аргумента.
Запишем в общем виде дифференциальное уравнение 1-го порядка [7], содержащее переменные y и x:
.
(3.20)
Решение уравнения (3.20) в функции от x найдем при условии:
,
когда
.
(3.21)
Из (3.20) получаем
,
следовательно,
.
(3.22)