Численные методы

ЛЕКЦИЯ 8 – 9

ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧ МАТЕМАТИЧЕСКОЙ ФИЗИКИ.

ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧ ДИСКРЕТНОЙ МАТЕМАТИКИ

Лекции 8 − 9

Численные методы решения задач математической физики

Численные методы решения задач дискретной математики

МАТЕМАТИЧЕСКАЯ ФИЗИКА

Математическая физика  теория математических моделей физических явлений; занимает особое положение и в математике и в физике, находясь на стыке этих наук. Математическая физика тесно связана с физикой в той части, которая касается построения математической модели, и в то же время математическая физика  раздел математики, поскольку методы исследования моделей являются математическими.

Математические модели физических явлений наиболее часто описываются при помощи дифференциальных уравнений с частными производными, получивших название уравнений математической физики. Помимо дифференциальных уравнений математической физики, при описании математических моделей физики применяются интегральные уравнения и интегро-дифференциальные уравнения, вариационные и теоретико-вероятностные методы, теория потенциала, методы теории функций комплексного переменного и ряд других разделов математики.

Уравнение с частными производными  это уравнение, содержащее частные производные. В отличие от обыкновенных дифференциальных уравнений (ОДУ), в которых неизвестная функция зависит только от одной переменной, в уравнениях с частными производными неизвестная функция зависит от нескольких переменных.

Приведем некоторые наиболее важные уравнения с частными производными. Для упрощения записи будем использовать следующие обозначения:

, , , . . . .

Некоторые уравнения с частными производными:

	(одномерное уравнение теплопроводности)
	(двумерное уравнение теплопроводности)
	(уравнение Лапласа в полярных координатах)
	(трехмерное волновое уравнение)
	(телеграфное уравнение)

Во всех приведенных примерах неизвестная функция u зависит более чем от одной переменной. Переменная u (которую мы дифференцируем) называется зависимой переменной. Переменные, по которым происходит дифференцирование, называются независимыми переменными. Например, в уравнении зависимая переменная u(x, t) является функцией двух независимых переменных x и t.

Большинство физических законов природы можно сформулировать на языке уравнений с частными производными. В качестве примеров можно привести уравнения Максвелла, закон теплообмена Ньютона, уравнения НавьеСтокса, уравнения движения Ньютона, уравнение Шредингера в квантовой механике. Во всех этих уравнениях физические явления описываются на языке пространственных и временных производных. Производные появляются в уравнениях потому, что они описывают важнейшие физические величины ( такие, как скорость, ускорение, сила, трение, поток, ток и т.д.).

Цель этого учебного пособия состоит в том, чтобы показать:

1. Как физическую задачу сформулировать в виде уравнения с частными производными (построение математической модели).

2. Как решить уравнение с частными производными (с учетом начальных и граничных условий).

Методы решения уравнений с частными производными

1. Метод разделения переменных. Уравнение с частными производными с n независимыми переменными сводится к n обыкновенным дифференциальным уравнениям.

2. Метод интегральных преобразований. Уравнение с частными производными с n независимыми переменными сводится к уравнению с частными производными с (n - 1) независимыми переменными; следовательно, уравнение с частными производными с двумя независимыми переменными можно свести к обыкновенному дифференциальному уравнению.

3. Метод преобразования координат. Исходное уравнение с частными производными сводится к обыкновенному дифференциальному уравнению или к другому, более простому уравнению с частными производными с помощью соответствующего преобразования координат (например, поворота координатных осей и т.п.).

4. Преобразование зависимой переменной. Исходное уравнение с частными производными преобразуется к такому уравнению с частными производными для другой неизвестной функции, которое решается легче, чем исходное.

5. Численные методы. Исходное уравнение с частными производными сводится к системе разностных уравнений, которая решается методом итераций на ЭВМ.

6. Метод теории возмущений. Исходная нелинейная задача сводится к последовательности линейных задач, аппроксимирующих нелинейную задачу.

7. Метод функций Грина. Начальные и граничные условия заменяются системой простейших источников, и задача решается для каждого простейшего источника. Полное решение исходной задачи получается в результате суммирования решений для элементарных источников.

8. Метод интегральных уравнений. Уравнение с частными производными сводится к интегральному уравнению. Существует много различных методов решения интегральных уравнений.

9. Вариационные методы. Вместо уравнения с частными производными решается некоторая задача минимизации. Оказывается, что функция, доставляющая минимум некоторому выражению является в то же время решением исходного уравнения с частными производными.

10. Метод разложения по собственным функциям. Решение уравнения с частными производными ищется в виде ряда по собственным функциям. Эти собственные функции находятся как решения так называемой задачи на собственные значения, соответствующей исходной задаче для уравнения с частными производными.

Тема. Численные и аналитические методы решения уравнений в частных производных. Построение разностных схем для уравнений в частных производных первого и второго порядка. Устойчивость решения разностных уравнений к малым изменениям начальных условий и правых частей. Сходимость решения разностного уравнения к точному решению исходного уравнения.

Построение разностных схем для уравнений в частных производных

Рассмотрим прямоугольную область

При решении задач разностным методом вводится разностная сетка (рис. 13), чаще всего равномерная, с координатами узлов , где ; – шаг по координате ; ( где ; - шаг по времени. Значения функции в узлах сетки обозначим = .

При численном решении уравнений в частных производных входящие в эти уравнения частные производные заменяют, на соответствующие им, конечно-разностные отношения. Полученное в результате такой замены уравнение называется разностной схемой или разностным уравнением. То есть, вместо решения исходного уравнения решается соответствующее ему разностное уравнение.

Отношения конечных разностей для частных производных строятся так же, как и для обычных производных

, , , , .

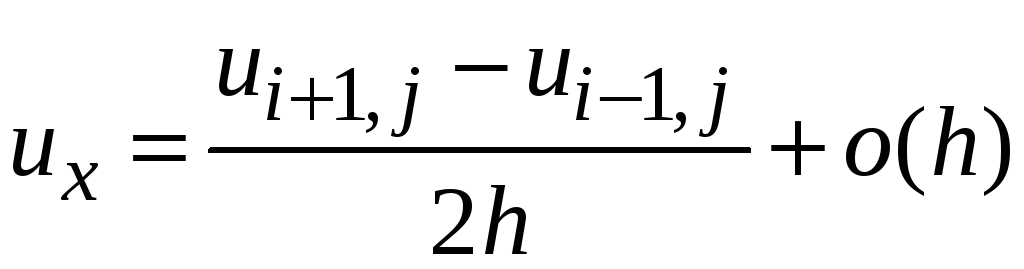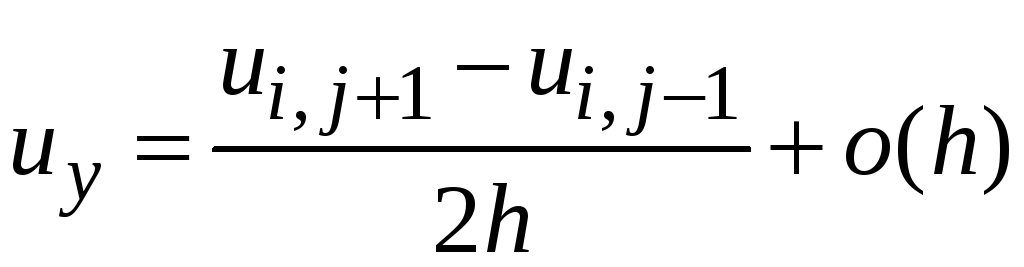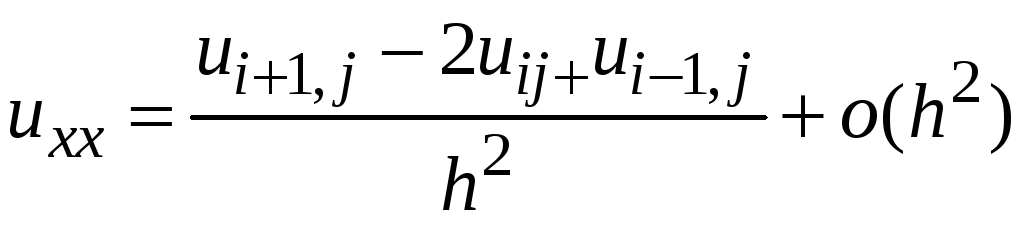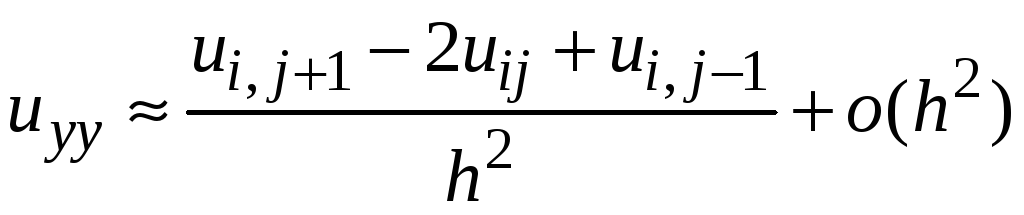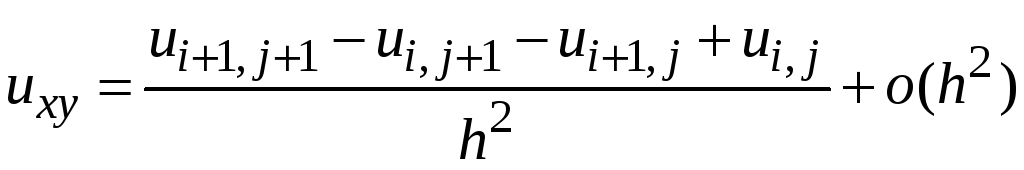Рассмотрим конкретный пример процесса теплопередачи по длинному стержню, лежащему вдоль оси от до . Предположим, что в точке температура задается функцией , а в точке функцией . Предположим также, что в момент времени распределение температуры вдоль стержня задавалось функцией . Тогда распределение температуры вдоль стержня во все последующие моменты времени дается решением уравнения

, (1)

где - температура стержня в данной точке в данный момент времени, а постоянная , – теплоемкость материала стержня, – плотность материала стержня и – его теплопроводность. Для простоты положим , так что уравнение сведется к следующему виду:

. (2)

Граничными и начальными условиями для этого уравнения являются

. (3)

. (4)

При решении задач разностным методом граничные и начальные условия определяются следующим образом

Заменяя в исходном уравнении (1) частные производные искомой функции с помощью отношений конечных разностей

; ,

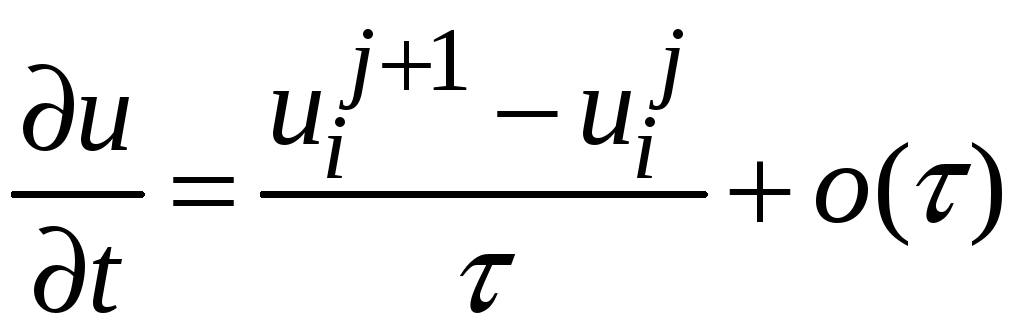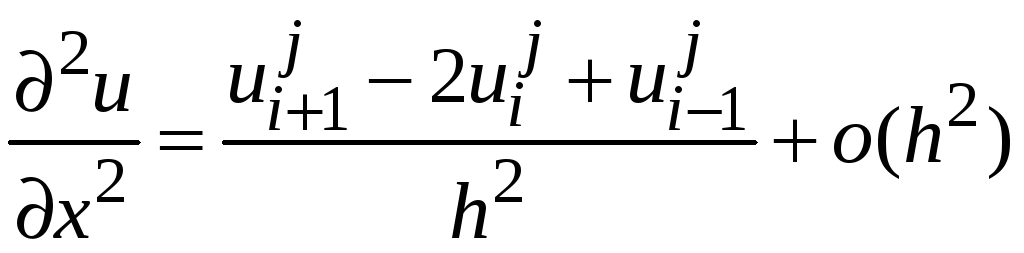получим разностную схему:

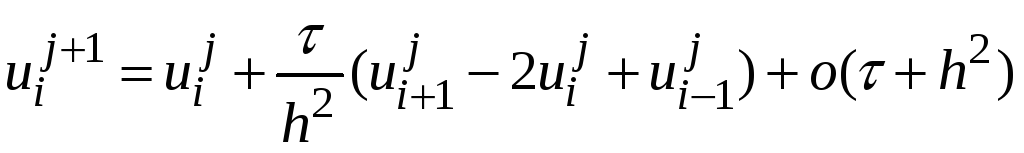. (5)

0

Пространственно-временная сетка

Это и есть разностное уравнение для уравнения теплопроводности, то есть соотношение, при помощи которого можно вычислить значения в данный момент времени через решение в предыдущий момент времени. Такие разностные уравнения, или разностные схемы, называются явными.

У явных схем есть серьезный недостаток. Если шаг по времени оказывается достаточно большим по сравнению с шагом по , погрешности округления могут стать настолько большими, что полученное решение потеряет смысл. Отношение шагов по t и x зависит от уравнения и граничных условий, но в общем случае должно выполняться условие устойчивости . Шаблон разностной схемы (5) изображен на рисунке.