Так как должны выполняться условия (3.21), (3.22) можно записать в виде

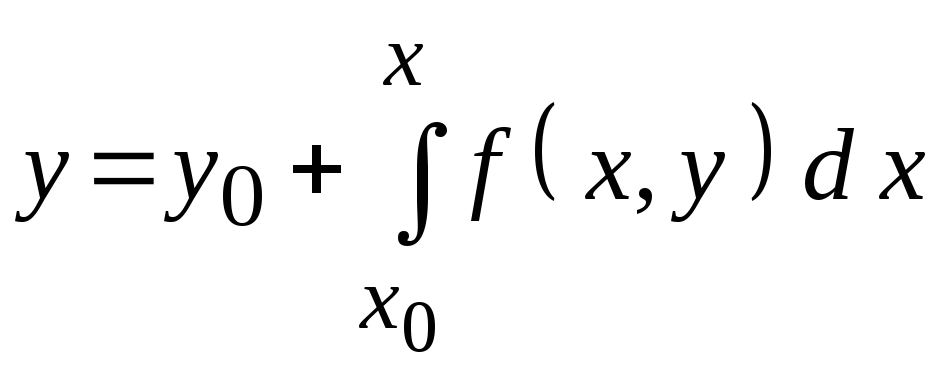. (3.23)

Интеграл в (3.23) представляет собой приращение y, которое нужно прибавить к , для того чтобы получить значение y, соответствующее какому-нибудь определенному значению x.

Очевидно, наша задача (отыскание y) затрудняется наличием y под знаком интеграла и в левой части выражения (3.23). Уравнение такого рода называется интегральным уравнением, которое можно решить методом последовательных приближений. С целью найти решение уравнения (3.23) необходимо воспользоваться тем обстоятельством, что вычислительная схема должна быть устойчивой, т.е. малому приращению аргумента (промежутку интегрирования) соответствующее приращение y тоже мало. Если функция y непрерывна, то это условие будет соблюдаться. Тогда, чтобы получить первое приближенное значение y, y под знаком интеграла заменим через :

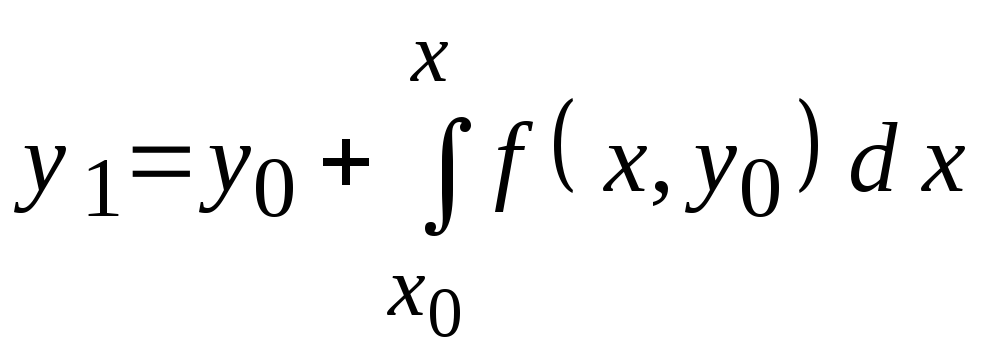Теперь подынтегральное выражение является функцией только x, поэтому интеграл может быть вычислен или непосредственно, или каким-либо приближенным путем.

Далее получаем:

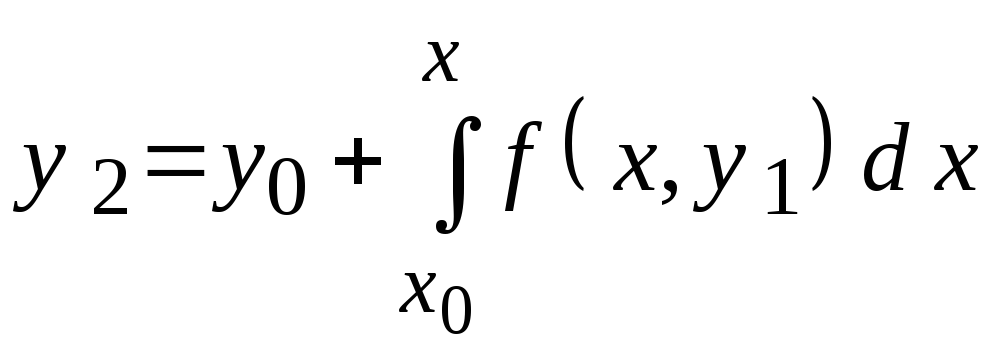и т.д.

Повторив этот процесс необходимое или желательное число раз, мы получаем n-е приближение в следующем виде:

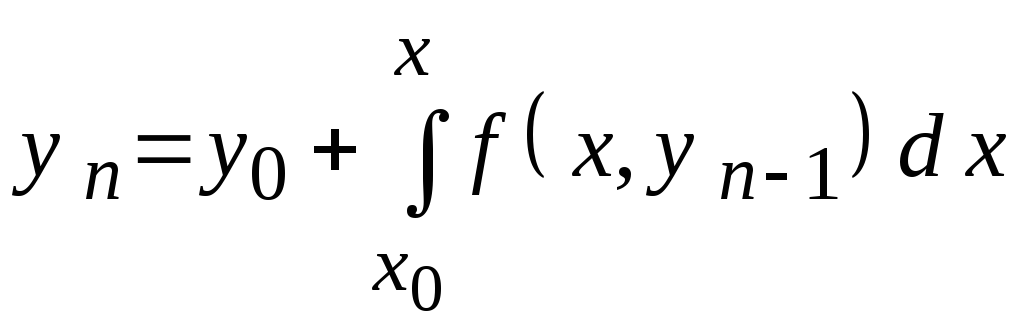(n = 1, 2, . . . ). (3.24)

(Обращаем внимание, что индексы обозначают степень приближения, а не какие-то порядковые номера.)

Пример 8. Найти решение дифференциального уравнения , удовлетворяющее начальным условиям , (заметим, что исходное уравнение при этих начальных условиях имеет точное решение в виде ).

Решение. Применяя формулу (3.24), получаем

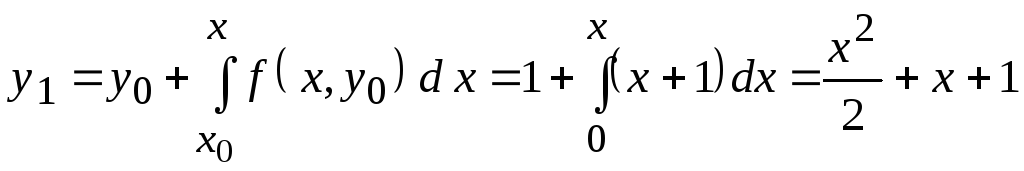продолжая аналогичным образом, можно получить и последующие приближения, т.е. , и т.д.

Пусть x = 0.1, тогда значение искомой функции для третьего приближения будет

Сравнение этого результата с точным ответом показывает, что значение точно до четырех десятитысячных знаков.

Замечания к методу Пикара.

Замечание 1. В методе последовательных приближений в качестве начального приближения можно выбирать любую функцию, достаточно близкую к точному решению y. Например, иногда выгодно в качестве брать конечный отрезок ряда Тейлора искомого решения.

Замечание 2. При пользовании методом последовательных приближений аналитичность правой части дифференциального уравнения не обязательна, поэтому этот метод можно применять и в тех случаях, когда разложения дифференциального уравнения в степенной ряд невозможно.

Замечание 3. Метод Пикара можно развить для системы дифференциальных уравнений.

Замечание 4. У этого метода, при всей своей привлекательности, имеются недостатки, а именно: во-первых, могут иногда попадаться несколько раз подряд трудные, а то и не берущиеся в элементарных функциях интегралы и, во-вторых, метод последовательных приближений может привести к громоздким вычислениям. Для этого рассмотрим следующие примеры.

Геометрически последовательные приближения представляют собой кривые (n = 1, 2, 3, …), проходящие через общую точку, приближающихся постепенно к точному решению y = y(x) (рис. 8).