Схемы второго порядка точности
Совершенно естественно, что человеку хочется считать уравнения с минимальными затратами. Один из способов достичь этого – повышение порядка точности разностных схем. Выигрыш достигается, во-первых, за счет уменьшения числа ячеек, на которых получается требуемая точность, во-вторых, за счет уменьшения числа шагов по времени. Особенно остро эти проблемы встают для параболических уравнений, где присутствуют ограничения на шаги по времени (и/или пространству).
Как получить аппроксимацию второго порядка по пространству ясно (это не раз проделывалось выше). Вопрос: как получить такую аппроксимацию по времени? Первый способ: использовать центральную разность. Для этого все производные по пространству должны иметь аппроксимацию второго порядка для точки, соответствующей моменту времени tj+/2. Такой подход реализуется, например, в схеме Кранка-Николсона. Для цветового уравнения
разностная схема записывается так
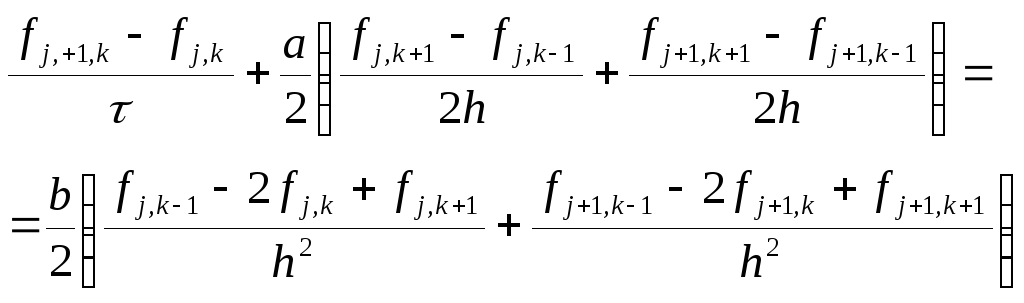
Шаблон разностной схемы выглядит так
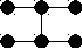
Как видно, это неявная схема. Для нахождения значений на новом слое необходимо решить систему линейных уравнений. Для одного пространственного измерения это просто. Матрица получается трехдиагональной. Система легко решается методом прогонки. Но в случае двух или трех пространственных измерений решение получаемой системы уравнений существенно затрудняется. Поэтому такая схема применяется редко.
Другой подход к получению аппроксимации второго порядка: использование некоторых промежуточных значений. Идея оказалась очень плодовитой. Доказано, что таких схем можно создать бесконечно много. Более того, существует нехитрый алгоритм позволяющий плодить такие схемы: подставляй значения параметров и получай новую схему (присваивай ей свое имя). Несмотря на такое многообразие, используемые на практике схемы можно перечесть по пальцам. В этом курсе рассмотрим две самые популярные.
Обе эти схемы двухшаговые. На первом шаге находятся некоторые вспомогательные значения. На втором шаге находятся окончательные значения. Первый шаг, как правило11, называют «предиктором», второй – «корректором»12. Поэтому такие схемы часто называют схемами типа «предиктор-корректор».
Сначала рассмотрим схему Лакса-Вендроффа. Возьмем уравнение
где F – некоторое выражение от искомой функции. Первый шаг записывается по схеме Лакса (см. задачу 12)
второй шаг записывается по схеме «чехарда» (см. задачу 13)
Графическое изображение имеет следующий вид
Для волнового уравнения первого порядка F=af. На каждом из этих шагов используется явная схема, уравнение линейное, поэтому можно написать явную схему и для окончательного результата.
Убедимся, что схема имеет порядок не менее второго. Найдем реально решаемое уравнение. При этом в разложении в ряд Тейлора оставим члены до второго порядка включительно.
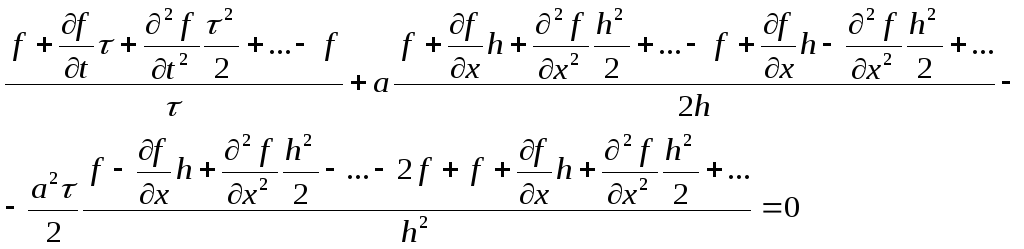
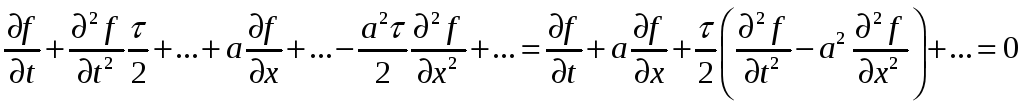
но, исходя из исходного уравнения, имеем
Таким образом, члены, дающие погрешности, пропорциональные шагам сетки, сокращаются.
Для цветового уравнения имеем
На предикторе можно использовать следующие соотношения13
при расчете
при расчете
а на корректоре использовать соотношения
Никаких ограничений, связанных только с физикой и задающих максимально возможные шаги, для данной схемы нет.
Другой (еще более распространенной) схемой второго порядка аппроксимации является явная схема Мак-Кормака14. Для волнового уравнения первого порядка первый шаг запишется по явной схеме «левый уголок»
второй шаг записывается аналогично неявной схеме «правый уголок», но с половинным шагом по времени
Естественно, с тем же успехом на первом шаге можно использовать явную схему «правый уголок», а на втором неявную «левый уголок». Аналогично схеме Лакса-Вендроффа запишем явный одношаговый аналог схемы МакКормака для волнового уравнения первого порядка.
То есть для данной постановки задачи обе эти схемы эквивалентны.
Для того, чтобы схема Мак-Кормака имела второй порядок аппроксимации и для цветового уравнения нужно использовать для F разности, обратные к используемым на шагах предиктора и корректора. То есть на предикторе считать
а на корректоре считать
