Спектральный метод (метод Фурье)

Спектральный метод, как и метод конечных элементов, является разновидностью метода Галеркина. В методе конечных элементов по сравнению с классическим методом Галеркина было существенно сокращено количество интегралов, которые нужно найти, за счет использования финитных функций. Но это не единственный способ. Можно подобрать такие функции, определенные на всей расчетной области, интегралы от произведения которых равны нулю. Такие наборы функций называются ортогональными. Известно много наборов таких функций, но рассмотрим самый известный из них – синусы и косинусы.

Вариант метода Галеркина, в котором в качестве пробных используются ортогональные функции, называется спектральным методом. Разложение функции по синусам и косинусам традиционно называется нахождением спектра. Отсюда, видимо, и название метода. Хотя, можно использовать и другие наборы ортогональных функций. В отличие от метода конечных элементов, в спектральном методе пробные функции могут принимать отличные от нуля значения во всей расчетной области.

Итак, ортогональными функциями называются функции, удовлетворяющие условию

На отрезке [-,] в качестве таких можно использовать функции:

1,cosx,sinx,cos(2x),sin(2x),…,cos(nx),sin(nx),…

При этом интеграл по данному отрезку от произведения любых двух различных функций из этого набора равен нулю. Интегралы от квадратов функций имеют вид:

С помощью нехитрого преобразования можно построить аналогичный набор функций для произвольного отрезка [a,b]:

1,, ,…,, ,…

Значения интегралов от квадратов функций изменяются при этом пропорционально длине отрезка. У такого набора функций (синусы и косинусы) есть еще одно преимущество (не всегда наблюдаемое у других наборов ортогональных функций): производные от них (с точностью до постоянных множителей) принадлежат тому же набору функций. Единицу иногда рассматривают как частный случай косинуса с нулевым коэффициентом перед аргументом.

Все остальное осталось от классического метода Галеркина. Рассмотрим, например, применение спектрального метода к уравнению

оно моделирует, например, остывание (прогрев) за счет теплопроводности или «рассасывание» за счет диффузии. Рассмотрим решение этого уравнения на отрезке [-L,L] с начальным условием

и граничными условиями: f(-L,t)=0 и f(L,t)=0. Будем искать решение в виде

продифференцировав данное выражение и подставив в исходное выражение, получаем

после сокращения получаем обыкновенное дифференциальное уравнение для функции c(t)

которое легко решается, в результате получаем решение

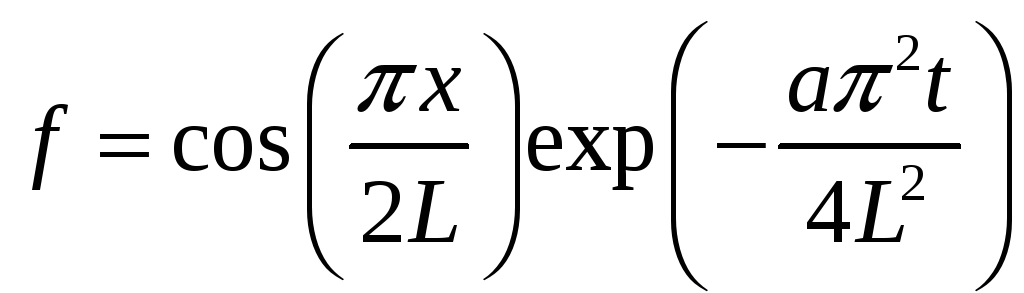
Рассмотрим случай более сложных начального и граничных условий. Пусть задано f(x,0)=(x), f(-L,t)=b₁ и f(L,t)=b₂. Тогда будем искать функцию в виде

Функцию f₀ можно выбрать так, чтобы она удовлетворяла граничным условиям, например

при таком выборе и первая производная f₀ по времени и вторая производная по пространству равны нулю. Следовательно, когда мы начнем искать, в соответствии с идеей метода Галеркина, интегралы от произведения невязки на пробную функцию, то (в силу ортогональности функций и того, что вторые производные выбранных тригонометрических функций пропорциональны самим функциям) получим уравнения, содержащие по одной единственной пробной функции. В результате получаем ряд задач, совершенно аналогичных ранее рассмотренной. Откуда, по аналогии, получаем

в результате решение исходного уравнения получается в виде

коэффициенты A_ci и A_si должны быть найдены из еще неиспользованного начального условия. Подставляя в начальное условие выражение для искомой функции, после переноса f₀ в левую часть, получаем

Отсюда видно, что искомые коэффициенты являются коэффициентами разложения функции -f₀ в ряд Фурье. На практике от бесконечных рядов оставляют только некоторое ограниченное количество членов. Таким образом, спектральный метод в ряде случаев позволяет существенно упростить решение задачи по сравнению с классическим методом Галеркина.

Спектральный метод, как правило, позволяет получить более высокую точность при том же числе неизвестных, чем метод конечных разностей (и большинство других сеточных методов). Однако, точность достигается значительными трудностями при вычислении невязок в нелинейных уравнениях и реализации граничных условий Неймана (когда на границе задано значение производной функции).

Естественно, у людей возникало желание совместить точность спектрального метода и простоту сеточных методов. Такие методы были созданы. Один из таких методов называется псевдоспектральным. По своей сути он ближе не к методу Галеркина, а к более простому в реализации методу коллокаций.

Метод предполагает наложение на расчетную область сетки и последующее послойное (по времени) нахождение значений функции в узлах сетки. На каждом шаге проделываются следующие действия:

1) нахождение разложения функции в сумму пробных на текущем слое (нахождение спектра). Эту операцию умеют делать быстро.

2) нахождение пространственных производных функции по разложению.

3) нахождение значений функции на новом слое по явной схеме первого порядка.

Рассмотрим, например, применение псевдоспектрального метода к уже рассматривавшейся задаче. Дано уравнение

Рассмотрим решение этого уравнения на отрезке [-L,L] с начальным условием

и граничными условиями: f(-L,t)=0 и f(L,t)=0. Шаг сетки примем равным L. Таким образом, сетка содержит всего 3 узла в направлении оси X. Из них в двух стоят граничные условия. Будем искать решение в единственном оставшемся узле.

Когда узлов побольше, то для нахождения разложения в сумму пробных функций обычно применяют быстрое преобразование Фурье. Оно работает быстро и надежно, но предполагает, что в разложении используются функции, имеющие целое число периодов на рассматриваемом отрезке. Ранее мы пользовались, в том числе, функцией имеющей период, вдвое превышающий рассматриваемый отрезок. Поэтому попробуем проводить учения в условиях, максимально приближенных к боевым, и искать разложение в виде

В момент времени t=0 имеем следующие значения функции в узлах: f(‑L,0)=0, f(0,0)=1, f(L,0)=0. Разложение будет выглядеть так

теперь оценим значения производных

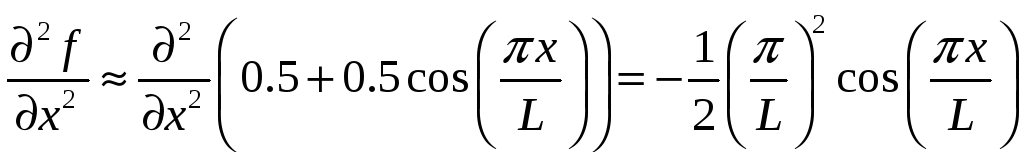
Следовательно, в единственном узле, где нам нужно найти производную по времени, имеем

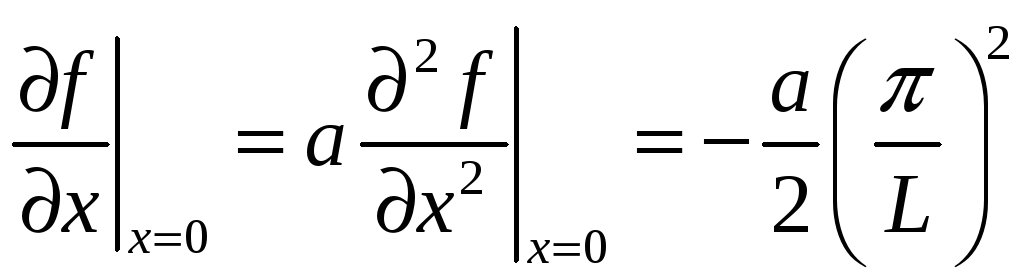
В момент времени t= получаем

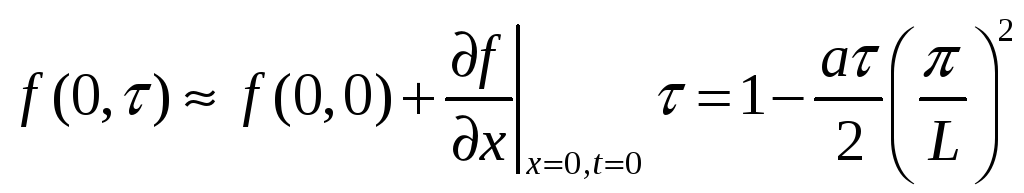
Далее процедура повторяется. На последок сравним полученный результат с результатом метода конечных разностей и теорией. Теория дает в этом же узле в начальный момент времени вдвое меньшее значение производной

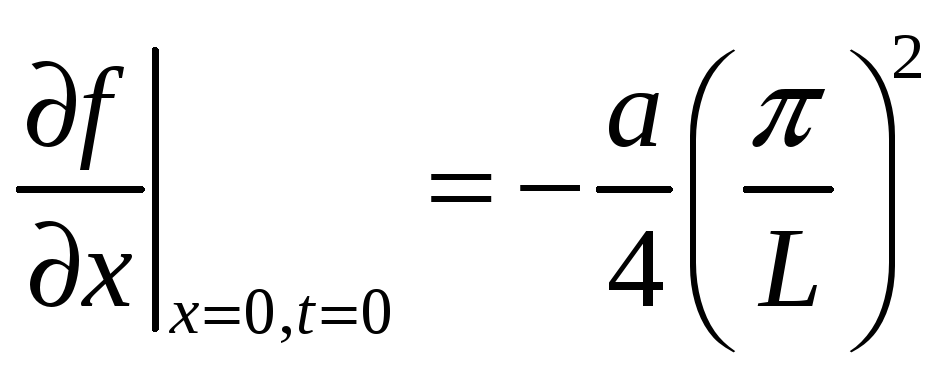
метод конечных разностей дает значение, отличающееся от теоретического примерно на четверть

Как видно, в данном случае, псевдоспектральный метод дал даже большую ошибку, чем метод конечных разностей. Что говорит о том, что он может сочетать не только достоинства спектрального и сеточных методов, но и их недостатки. Поэтому применяется сравнительно редко. В большинстве случаев псевдоспектральный метод эквивалентен методу конечных разностей с большим порядком аппроксимации по пространству и первым порядком по времени.

На этом с методами взвешенных невязок в рамках этого курса покончено.