Метод граничных элементов24

В ряде случаев удается упростить (с точки зрения объема вычислений) задачи, сведя их к задачам меньшей размерности. Например, решение трехмерной задачи свести к решению двумерной задачи. Обычно, это удается сделать, если процессы, проходящие внутри расчетной области достаточно просты. Например, это иногда удается сделать при расчете нейтральных частиц в разреженной плазме (где движение частиц можно считать прямолинейным). Но для применения этого метода необходимо еще одно условие. Угол, под которым частица отлетает от стенки, не зависит от предыстории (например, от угла, с которым частица подлетала к стенке). Суть метода состоит в том, что задачу о распределении нейтральных частиц в расчетной области сводят к решению задачи о распределении потоков нейтральных частиц с границ. То есть трехмерную задачу сводят к двумерной или двумерную задачу сводят к одномерной.

На ячейки в этом методе делится не расчетная область, а ее граница. В каждой такой ячейке нужно найти массовый поток нейтральных частиц, идущих со стороны границы. Для простоты будем считать, что все нейтральные частицы имеют одну скорость (в противном случае нужно заводить несколько групп нейтральных частиц, различающихся скоростью частиц). Ячейки, относящиеся к выходу рассчитываемого устройства, можно, как правило, исключить из расчета – через них в расчетную область нейтральные частицы не поступают, а только уходят. А для всех прочих ячеек составляются уравнения баланса массы. Искомый массовый расход в сторону объема рассчитываемого устройства через ячейку приравнивается сумме потоков: массовый расход подаваемого рабочего тела (если оно подается через данную ячейку), массовый поток ионов на эту ячейку и массовый расход частиц, пришедший с других ячеек. Для j-й ячейки это выглядит так

Получаем систему линейных алгебраических уравнений. В матричном виде ее можно записать

где элементы вектор-столбца B представляют собой суммы потоков ионов и расхода газа через ячейки, вектор-столбец M является искомой величиной. На главной диагонали матрицы A стоят единицы, а на месте с индексами j и i стоят со знаком минус доли расходов с одной i-й ячейки, приходящие на j-ю ячейку.

Доля частиц, вылетающих с одной площадки (ячейки) и приходящих на другую, определяется законом разлета частиц и вероятностью преодоления ими расстояния между площадками. Если частицы равновероятно разлетаются по всем возможным направлениям, то долю частиц, вылетевших с i-й площадки в сторону j-й, можно оценить по формуле

где S_j – площадь j-й ячейки, _j,i – угол между нормалью к j-й площадке и линией, связывающей центры i-й и j-й площадок, R_i,j – расстояние между двумя центрами площадок. Потери нейтральных частиц вследствие ионизации тоже легко оцениваются. Для этого пройтись вдоль линии, соединяющей площадки, и проинтегрировать все потери. В результате вероятность того, что частицы долетят, будет

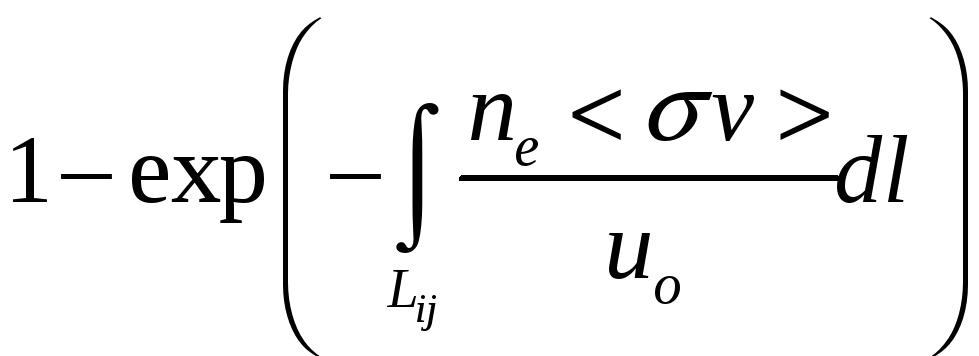
Окончательно внедиагональные элементы матрицы A можно записать

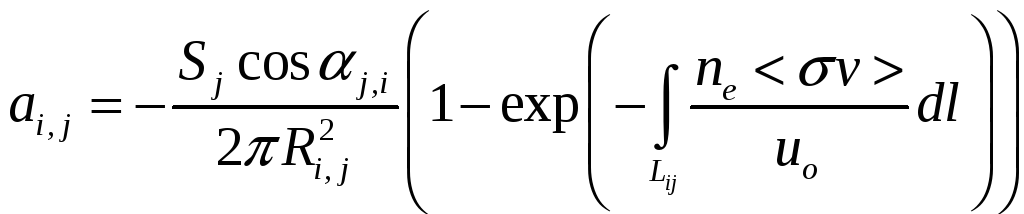
Теперь решаем систему линейных уравнений и получаем потоки нейтральных частиц со стенок. Но нам нужны концентрации нейтральных частиц внутри расчетной области. Оказывается, это довольно просто. В любой точке пространства мы можем посчитать концентрацию частиц прилетающих с каждой площадки. Если бы частицы, летящие с i-й площадки, не выбывали из-за ионизации, то их концентрация в точке с индексом p составила бы

но вероятность того, что они в эту точку долетят, составляет

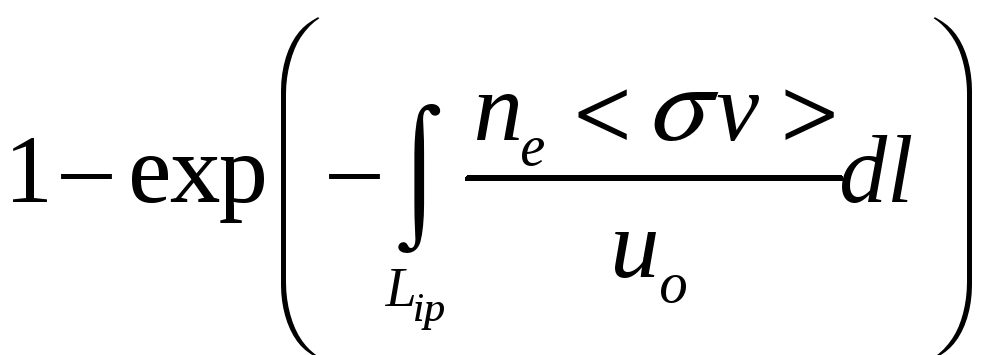
Следовательно, окончательно формула для концентрации будет выглядеть так

За счет того, что решается задача меньшей размерности, этот метод (там, где его можно применить) позволяет существенно сократить время счета.

На этом курс закончен. Спасибо за внимание.

Задачи

0. Как вычисляется количество чего-либо в объеме? Как вычисляется поток чего-либо через поверхность?

1. Записать в безразмерном виде уравнение сохранения массы

Решение. В безразмерном виде данное уравнение записывается

где Sh= - число Струхаля, характеризующее нестационарное движение.

2. Записать в безразмерном виде уравнение сохранения импульса электронов.

Решение. В безразмерном виде уравнение записывается

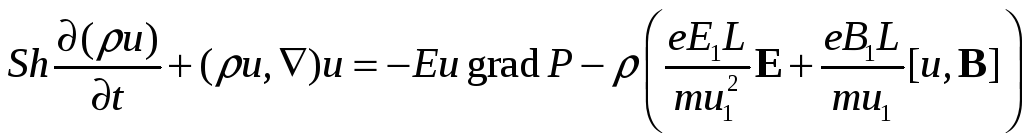
где Eu – число Эйлера.

3. Записать в безразмерном виде уравнение ламинарного пограничного слоя

Решение. В безразмерном виде уравнение записывается

где Re= - число Рейнольдса

4. Оценить концентрацию нейтральных частиц в устройстве. Полость цилиндрической формы 10 см в длину и 10 см в диаметре. С одного торца подается ксенон (атомная масса 131) 0.5 мг/с. Другой торец - отверстия, суммарная площадь которых 0.9 от площади торца. Скорость истечения оценивать по формуле . Температура нейтральных частиц 600 К. Справочные константы: масса нейтрона 1.6710^-27 кг, постоянная Больцмана 1.3810^-23 Дж/кг.

Ответ: 3.810¹⁸ м^-3.

5. В предыдущей задаче оценить концентрации ионов и нейтральных частиц в камере. Считать, что 70% потока массы уходит в виде ионов (коэффициент использования рабочего тела 70%). Скорость ионов в камере оценивать по формуле . Температура электронов соответствует энергии 8 эВ. Заряд электрона 1.610^-19 Кл.

Ответ: концентрация нейтральных частиц 1.1510¹⁸ м^-3, концентрация ионов 1.310¹⁷ м^-3.

6. В задаче 5 вместо заданного коэффициента использования рабочего тела заданы интенсивность ионизации <v>=510^-14 м³/c и коэффициент использования объема для процесса ионизации 0.5. Определить коэффициент использования рабочего тела.

Ответ: 82%

7. Для задачи 6 построить зависимость коэффициента рабочего тела для изменения расхода от 0.5 до 0.7 мг/с.

Ответ: 82%-87%.

8. Численно решить уравнение

используя следующую разностную схему

на отрезке 0x20 с шагом 1 и 0t15 с шагами 0.5, 0.75 и 1. Начальное распределение

и граничном условии f(t,0)=1.

Ответ: аналитическое решение

9. Численно решить уравнение

используя следующую разностную схему

на отрезке 0x1 с шагом 0.1 и 0t0.2 с шагами 0.005 и 0.01. Начальное распределение

и граничных условиях f(t,0)=f(t,1)=0.

Ответ: аналитическое решение

При шаге по времени 0.01 наблюдается потеря устойчивости

10. Численно решить невязкое уравнение Бюргерса

используя следующую разностную схему

на отрезке 0x30 с шагом 1 и 0t25 с шагом 1. Начальное распределение

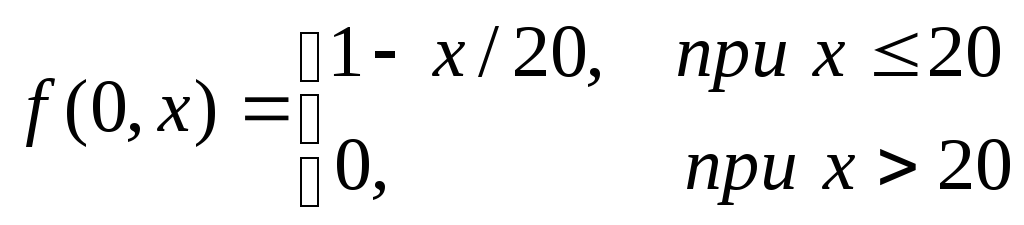
и граничном условии f(t,0)=1.

Ответ: аналитическое решение

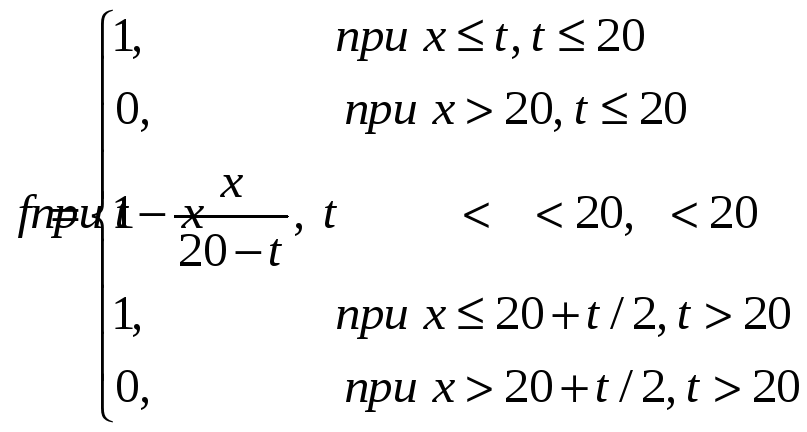
11. Исследовать устойчивость разностной схемы методом дискретного возмущения

Ответ: схема неустойчива (устойчива только при a=0)

12. Исследовать устойчивость разностной схемы (схемы Лакса) методом дискретного возмущения

Ответ: схема устойчива при |C|1.

13. Исследовать устойчивость разностной схемы (схемы «чехарда» Дюфорта-Франкела) методом фон Неймана

Ответ: схема устойчива при |C|1.

14. Получить приближенные решения дифференциального уравнения

с начальным условием f(0)=1. Решение искать на отрезке [0,1] в виде

Использовать методы: коллокаций (узлы на концах отрезка), наименьших квадратов и Галеркина. На одном графике построить все полученные решения в сравнении с аналитическим решением и рядом Тейлора (первые три члена разложения). На одном графике построить погрешности трех полученных решений и Тейлора.

Ответ: метод коллокаций

Метод наименьших квадратов

Метод Галеркина

15. Методом конечных элементов решить дифференциальное уравнение

с начальным условием f(0)=1 на отрезке [0,1] с шагами 1, 0.5 и 0.25. Построить зависимость погрешности в точке x=1 от шага.

Ответ: при h=1: f(1)=2/5, -0.032

При h=0.5: f(1)=25/59, 0.0053

При h=0.25: f(1) 0.369, 0.0014

16. Методом конечных элементов решить дифференциальное уравнение Пуассона

на отрезке [-1,1] с граничными условиями f(-1)=0 и f(1)=0 с шагами 1 и 0.5. Построить график функции.

Ответ: f(-0.5)=0.75, f(0)=1, f(0.5)=0.75

17. Методом конечных элементов решить дифференциальное уравнение Пуассона

на отрезке [-1,1] с граничными условиями f(-1)=0 и f(1)=0 с шагами 1 и 0.5. Построить график функции.

При нахождении решения можно пользоваться формулой для внутренних узлов

Ответ: для h=1: f(0)=1

Для h=0.5: f(-0.5)=0.9375, f(0)=1, f(0.5)=0.9375

18. Методом Монте-Карло без использования весов посчитать коэффициент использования рабочего тела. Вероятность ионизации частицы при пролете устройства 0.4, ионизовавшаяся частица покидает устройство. На одном конце подается рабочее тело, вероятность вылета нейтральной частицы, достигшей другого конца, равна 0.3. Использовать 20 частиц.

Ответ: аналитическое решение 0.759.

19. Предыдущую задачу посчитать Методом Монте-Карло с использованием весов. Использовать одну частицу. Остановить, при значении веса, меньшем 10^-4.