Методы частиц

Методы частиц представляют собой очень большую и разнообразную группу методов. К решению практически любой физической задачи можно применить какой-нибудь метод из этой группы. Эти методы, как правило, имеют довольно простую физическую интерпретацию и могут быть относительно легко реализованы. Много полезной информации по этим методам можно найти в книге [11].

Начнем с простейших случаев. В простейших методы частиц являются частными случаями методов Монте-Карло (теперь чаще используют термины «прямое моделирование» и «имитационное моделирование»). Такие методы применяются при численном моделировании процессов в разреженной плазме. При этом в расчетной области отслеживается поведение некоторого числа частиц, каждая из которых движется по законам какой-либо физической частицы (нейтральной, иона или электрона). Взаимодействие между частицами происходит, когда они сближаются на расстояние, меньшее радиуса взаимодействия (в расчете он больше физического, т.к. расчетных частиц меньше, чем в реальном устройстве).

Наблюдение за частицами, конечно, интересное занятие, но нашей целью является вычисление параметров плазмы, например концентраций частиц в различных точках расчетной области. К тому же, зная параметры плазмы гораздо проще отслеживать взаимодействие частиц.

Рассмотрим расчет концентраций. Для этого задаем в расчетной области сетку (разбиваем на ячейки) и ищем концентрацию в каждой ячейке. В замкнутом объеме это проделывается очень просто. Число тяжелых частиц (нейтральных и ионов) там известно. Число расчетных частиц, которые мы пустили в этот объем тоже известно. Обозначим число физических частиц N_p и число расчетных частиц N. Тогда, если в j-й ячейке с объемом V_i находится N_i частиц, то концентрация равна

В случае, если через рассматриваемый объем есть расход рабочего тела, то расчет несколько усложняется. Рассмотрим стационарный случай. Пусть задан массовый расход . Мы запускаем в объем N частиц. Попутешествовав немного внутри расчетной области, они все должны вылететь за ее пределы. Но, пока они этого не сделали, нужно набрать статистику, которая будет использоваться в дальнейшем для расчета концентрации. Существуют два подхода к подсчету этой статистики: один попроще, второй поточнее. Начнем с первого. В нем фиксируется число пролетов частиц через ячейку. В итоге, когда все частицы покинут расчетную область, для каждой ячейки будем иметь число, показывающее, сколько раз частицы пролетали через эту ячейку. Обозначим такие числа N_j. Значит через j-ю ячейку пролетает массовый поток

но такой массовый поток можно оценить как

где - средний модуль скорости частиц, а S_j – площадь поверхности ячейки. Отсюда получаем плотность частиц в ячейке

Этот метод достаточно прост, но оценка массового потока через среднюю скорость частиц вносит дополнительную ошибку. Если среднюю скорость нейтральных частиц можно, как правило, считать заранее известной, то среднюю скорость частиц других видов нужно считать, опять же накапливая статистику.

Этих неприятностей можно избежать, если собирать чуть более сложную статистику во время расчета движений частиц. Для каждой ячейки нужно суммировать время, которое пролетающая частица провела внутри этой ячейки. Это время вычисляется по формуле

где l­ – длина пути, который частица прошла внутри ячейки, v – скорость, с которой частица пролетала этот участок. Обозначим за t_j суммарное время, которое частицы провели в j-й ячейке. Тогда формула для концентрации легко выводится. Выбранное нами общее число частиц влетает в расчетную область за время

За такой промежуток времени в j-й ячейке частицы провели время t_j. Следовательно, число находившихся там частиц равно

и концентрация равна

Для того, чтобы посчитать не только концентрацию, но и другие параметры (компоненты скорости, среднюю энергию частиц), нужно также накопить соответствующую статистику. Например, чтобы узнать среднюю энергию частиц, нужно для каждого пролета кроме времени, проведенного частицей в ячейке, посчитать произведение этого времени на энергию частицы. Обозначим сумму произведений времени на энергию как (t)_j, тогда средняя энергия считается по формуле

Еще проще выглядят формулы для средних значений компонент скорости. Умножая время на компоненту скорости, мы, естественно, получаем расстояние. То есть суммировать надо разности координат точек входа частицы в ячейку и выхода из ячейки. Компоненты средней скорости получаются делением суммы расстояний (разностей координат) на сумму времен.

Зная параметры плазмы в каждой ячейке, мы можем легко решать вопрос о вероятности взаимодействия частиц между собой. Теперь нам не надо рассматривать все возможные пары частиц на предмет: а не провзаимодействовали ли они? С учетом того, что обычно меньше ста тысяч частиц не рассматривают, отказ от рассмотрения всех пар приводит к существенной экономии времени. Теперь можно использовать ранее рассмотренную формулу о вероятности взаимодействия частиц. Вероятность того, что частица первого вида пройдет расстояние L в области, заполненной частицами второго вида равна

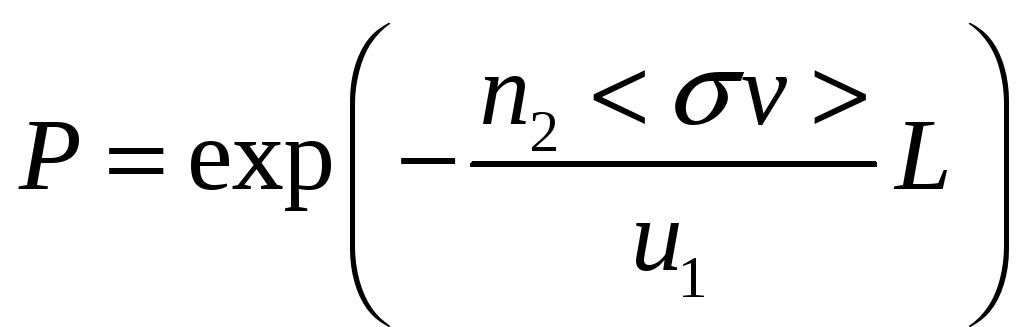
На участке траектории частицы, проходящем через ячейку, оценивается вероятность взаимодействия с другими частицами. Затем берется случайное число от нуля до единицы. Если случайное число меньше, чем вероятность взаимодействия, то считается, что взаимодействие произошло. Последствия этого могут быть самые разнообразные. Например, если под взаимодействием понималось упругое соударение (рассеяние одних частиц на других), то частица просто сменит траекторию (возможно, и энергию). Если имелось ввиду какое-либо иное взаимодействие (например, ионизация), то частица может перейти из одной группы в другую (например, из нейтральных в ионы).

Если рассматривается только одна группа частиц (например, нейтральные частицы), то точность можно еще поднять без существенных усложнений алгоритма. Для этого нужно считать, что то, что мы до сих пор называли частицей, не одна частица, а некоторое количество частиц. Тогда при прохождении какого-то участка часть из этого количества провзаимодействовала с другими частицами, а часть пошла дальше.

Возвращаясь к рассмотренным нами алгоритмам, припишем каждой частице еще одно число – так называемый вес (к массе и силе тяжести не имеющий никакого отношения). В начальный момент все веса равны единице. При пересечении частицей какой-либо ячейки этот вес умножается на вероятность благополучного (без взаимодействия) прохождения этого участка. Теперь появился еще один критерий для прекращения слежения за частицей. Отслеживание частицы прекращается не только в случае покидания ею расчетной области, но и в случае, когда ее вес стал меньше какой-то наперед заданной малой величины. При накоплении статистики все суммируемые величины будем умножать на вес частицы.

Продемонстрируем на примере расчет без весов и с весами. Рассмотрим одномерную модель газоразрядного устройства. С одного конца в него подается рабочее тело, все частицы, долетевшие до другого конца, покидают устройство. Проходя вдоль устройства, нейтральная частица с вероятностью p_i ионизируется и покинет устройство в виде иона. Требуется найти долю частиц, покидающих устройство в виде ионов. Очевидно, ответ будет p_i. Теперь попробуем получить результат классическим методом Монте-Карло. Для этого берем некоторое число частиц. Каждой из них ставим в соответствие случайное число от 0 до 1. Если число меньше p_i, то частица ионизуется, если больше – нет. Мы, конечно же, получим ответ, но приближенный. Чтобы повысить точность вдвое, нужно в четыре раза увеличить число частиц. Если же мы будем приписывать частицам веса, то нам достаточно пустить одну единственную частицу, она с вероятностью p_i ионизуется. Следовательно, к выходу придет нейтральная частица с весом (1‑p_i). Таким образом, мы с помощью одной частицы получили точный результат. К сожалению, в более сложных задачах одной частицей обойтись не удается.

Но борьба за точность при этом не остановилась. Дело в том, что существенные трудности возникают при попытках расчета потенциала плазмы. Если пытаться получить его традиционным способом (решая уравнение Пуассона), то нужно знать разность концентраций ионов и электронов. Даже в разреженной плазме концентрации ионов и электронов отличаются в пятом-седьмом знаке. Чтобы получить подобную точность методами Монте-Карло нужно в каждой ячейке иметь, как минимум, порядка 10⁵-10⁷ частиц. С учетом того, что ячеек должно быть, как минимум, сто в двумерном случае и 1000 в трехмерном, такая задача становится неподъемной для современных компьютеров (или будет решать неоправданно долго). К тому же классические методы Монте-Карло не дают повторяемости результатов. Несколько раз посчитав одну и ту же задачу, мы получаем несколько ответов (отличия между ними определяются погрешностью расчетов).

Попытки решения этих проблем привели созданию методов частиц конечного размера²¹. Вместо отдельных частиц в них рассматриваются некоторые пространственные образования (сгустки, облака) состоящие из частиц одного вида с близкими энергиями и направлениями движения. Для краткости эти образования опять называют частицами.

Наиболее часто встречающийся вариант этих методов выглядит следующим образом. Каждая частица занимает ровно одну ячейку (в ячейке может быть много частиц, различающихся видом, энергией и направлением движения). Рассматривают движение всех частиц в течение короткого промежутка времени такого, чтобы они не улетели дальше соседних ячеек. Затем в каждой ячейке составляется баланс: сколько чего убыло, сколько чего прибыло и сколько чего стало. Все, что стало в ячейке, разделяется на частицы, и процесс повторяется.

Для демонстрации данного метода рассмотрим одномерную задачу для нейтральных частиц. Будем обозначать концентрации частиц, движущихся влево и вправо в j-й ячейке, как n_j,l и n_j,r. Будем считать скорости всех частиц равными u. Размеры всех ячеек равны h. Частицы выбывают из расчетной области вследствие ионизации. Ионизация характеризуется величиной n_e<v>. Рассмотрим, что произойдет через время . Все частицы сместятся на расстояние u. Концентрация в каждой частице изменится в exp(-n_e<v>) раз. Каждая частица частично перейдет в соседнюю ячейку, вышедшая доля составит u/h. В j-й ячейке концентрация частиц, летящих влево составит

аналогично подсчитывается концентрация частиц, летящих вправо

Таким образом, можно рассчитать концентрации в следующий момент времени. Повторяя эту процедуру можно получить требуемое решение. Следует отметить, что здесь уже нигде не используется датчик случайных чисел. Это приводит к тому, что при таком подходе точность растет обратно пропорционально размеру частиц (а не корню из числа частиц, как в классических методах Монте-Карло).

В двумерном или трехмерном случае применяя эту идею получаем метод дискретных направлений. Из всего многообразия направлений выделяем конечное число фиксированных направлений, каждое из которых задает некоторый сектор или телесный угол. В каждой ячейке рассматриваются столько «сгустков», сколько выбрано направлений. (Все частицы, оказавшиеся в данной ячейке и движущиеся внутри некоторого сектора или телесного угла, относятся к соответствующему направлению.) На каждой итерации рассчитывается новое значение концентрации частиц в каждой ячейке и приписанных к каждому из направлений. Недостатком этого метода является «рассеивание» частиц (фактически частицы не могут двигаться по прямой, даже если на них не действуют никакие силы). Поэтому этот метод обычно применяется в тех случаях, когда длина пробега частиц меньше размера расчетной области.

Все изложенные выше методы частиц применимы к разреженной плазме (точнее: когда длина свободного пробега частиц больше размера ячейки). Если же длина свободного пробега частиц меньше размера ячейки, то можно считать, что каждый вид частиц имеет в ячейке один единственный вектор скорости – среднюю скорость физических частиц. Отдельные физические частицы отслеживать уже не имеет смысла. Используется идеология частиц конечного размера. То есть рассматриваются некоторые сгустки, которые, для краткости, тоже называют частицами. Во всех методах частиц для плотной плазмы расчетная область разбивается на ячейки, в которых и находятся параметры плазмы.

Рассмотрим методы частиц, применяющихся для расчета плотной плазмы, в порядке их появления. Сначала появился метод «частица в ячейке». В нем отслеживается движение некоторого количества частиц. Каждая частица имеет свою массу, вектор скорости, энергию. Размер частиц в данном методе не рассматривается, отслеживается лишь перемещение центра частицы. Имеем некоторое начальное распределение частиц. Через некоторый промежуток времени (он выбирается таким, чтобы частицы не успели пролететь расстояние, большее размера ячейки) все частицы изменят свое положение и параметры. Каждая из частиц окажется внутри какой-то ячейки. В каждой ячейке подсчитываются суммарные масса и энергия частиц каждого вида. Суммарная энергия частиц каждого вида внутри ячейки перераспределяется между этими частицами пропорционально массе. В ячейке вычисляется средний вектор скорости частиц каждого вида. Всем частицам одного вида внутри ячейки приписывается рассчитанная средняя скорость. Таким образом, получаем новое распределение частиц с новыми значениями параметров. Далее процесс повторяется до достижения требуемого критерия останова.

Следующим шагом люди подумали, зачем иметь несколько частиц в одной ячейке, если их параметры все равно осредняются. И придумали метод «жидких частиц²²». Каждая частица в этом методе занимает одну ячейку. Частицы имеют тот же набор параметров. Точно также рассматривается движение частиц на некотором промежутке времени. Если нас не очень интересуют процессы диффузии, то изменением размера частиц во время движения пренебрегаем. В следующий рассматриваемый момент времени каждая частица частично (или даже полностью) окажется в соседних ячейках, принеся туда соответствующие доли своих массы, импульса и энергии. Для каждой ячейки подсчитываются массы, импульс и энергия частиц каждого вида, которые в ней оказались (что-то осталось от «родной» частицы, что пришло из соседних ячеек). После чего о существовавших частицах забывают и в каждой ячейке «формируют» новые частицы (по одной каждого вида) с полученными параметрами.

Но потом люди еще подумали и сократили объем вычислений без потери точности. Получился метод крупных частиц²³. От частиц в нем почти ничего не осталось. Основная идея этого метода такая же, как и в методе конечных объемов. Но потоки массы, импульса и энергии через границы ячейки считаются по той же идеологии, как и в методе жидких частиц. Итак, в некоторый момент имеем в каждой ячейке для каждого вида частиц обычный набор параметров: плотность, вектор скорости, средняя энергия. Рассмотрим некоторый промежуток времени. За это время на содержимое ячеек будут действовать какие-то силы, определяемые выбранной нами физико-математической моделью. Эти силы повлияют на скорости в ячейках. Нам нужно определить средние (за выбранный промежуток времени) скорости и для каждой грани ячеек определить направление движения частиц каждого вида. Теперь можно посчитать потоки массы, импульса и энергии через эти грани. Потоки определяются средними (за выбранный промежуток времени) значениями параметров в ячейке, из которой они выходят (значения в ячейке, куда идет поток, не участвуют в расчете потока через грань). Зная все эти потоки нетрудно вычислить значения параметров плазмы в каждой ячейке в следующий момент времени. Далее весь этот процесс повторяется до тех пор, пока не будет решение об остановке. Для стационарных задач, как правило, расчет останавливают, если решения на двух последовательных итерациях отличаются на величину, меньшую заранее выбранного малого числа.

В простейших случаях (равномерная прямоугольная сетка) метод крупных частиц эквивалентен методу конечных разностей первого порядка типа «уголок» с автоматическим выбором разностной схемы из условия устойчивости. Поэтому единственным требованием к устойчивости метода крупных частиц является удовлетворение условия Куранта-Фридрихса-Леви.