Метод конечных элементов

Метод конечных элементов изначально разрабатывался для прочностных расчетов. Там он и сейчас является самым массовым методом. Позже отдельные его разновидности получили широкое распространение и в других областях. Здесь рассмотрим формулировку Галеркина, получившую наибольшее распространение (по крайней мере за пределами прочностностных задач).

В рассматриваемой формулировке метод конечных элементов можно рассматривать как частный случай метода Галеркина. От классического варианта метода Галеркина его отличает, главным образом, то, что в качестве пробных используются непрерывные финитные функции, т.е. функции равные нулю везде, кроме конечной области. Кроме того, каждая из этих функций в некоторой узловой точке равна единице, а в остальных узловых точках она равна нулю. Здесь возникает еще одно отличие от классической формулировки метода Галеркина: коэффициенты в разложении искомой функции приобретают конкретный физический смысл – это значения этой самой функции в узлах. Итак, функция ищется в виде

где f_j(t) – приближенные значения искомой функции в узлах, а _j(x,y,z) – пробные функции. Пробные функции (называемые также интерполяционнымии или функциями формы), как правило, выбираются из числа кусочно-линейных (или полилинейных).

Рассмотрим сначала одномерный случай. Кусочно-линейные пробные функции при этом будут иметь вид:

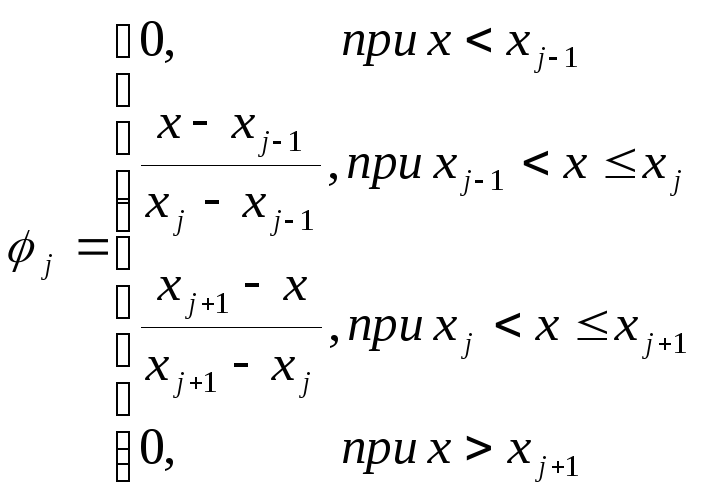
Представим эти функции графически, получаем

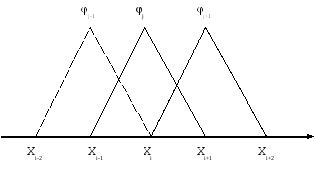
Очевидно, что при таком выборе пробных функций целевая функция будет между узлами интерполироваться линейно. Гораздо реже можно встретить вариант с квадратичной интерполяцией. При этом «четные» и «нечетные» пробные функции будут записываться по-разному. Не буду записывать формулы (желающие могут написать их самостоятельно), приведу рисунок.

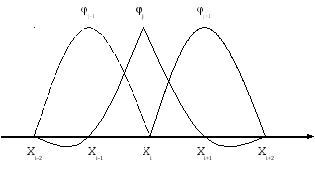
Использование квадратичной интерполяции повышает порядок аппроксимации получаемого решения, но заметно усложняет процесс нахождения его нахождения (особенно для двумерных и трехмерных случаев).

Рассмотрим двумерный случай. Наложим на расчетную область треугольную или прямоугольную сетку. Каждая пробная функция будет задана на ячейках, содержащих какой-то узел сетки. Тогда для каждого конечного элемента (области, где пробная функция отлична от нуля) легко записать пробную функцию. В центральном узле она равна единице, а на периферии нулю. В каждой из ячеек мы можем написать линейную или билинейную функцию, которая будет удовлетворять этим условиям. Так для треугольной области напишем

а для прямоугольной

Для трехмерного случая принцип построения пробных функций точно такой же.

Научившись выписывать пробные функции можно выписать систему уравнений, которую предстоит решать. Как и в классическом методе Галеркина это будут уравнения вида

Так как использовались финитные пробные функции, то каждое из этих уравнений будет содержать лишь ограниченное число неизвестных.

Рассмотрим теперь применение на конкретном примере. Прежде, чем рассмотрим применение метода конечных элементов, решим задачу, которая нам еще не раз понадобится.

Задача: в направлении оси X идет пучок частиц первого вида. Все частицы имеют одинаковую скорость. Эти частицы могут сталкиваться с частицами второго вида, при этом частицы первого вида переходят в некоторое другое состояние или превращаются в другие частицы (например, вследствие ионизации, рекомбинации, возбуждения или чего-нибудь еще). Скорость частиц первого вида считаем неизменной. Вопрос: как меняется вдоль оси X концентрация частиц первого вида в начальном состоянии?

Чтобы получить ответ нужно решить в одномерной постановке уравнение сохранения массы.

где величина <v> характеризует интенсивность взаимодействия частиц разных видов. В силу неизменности скорости первых частиц получаем простое дифференциальное уравнение относительно концентрации

Такое уравнение легко решается аналитически

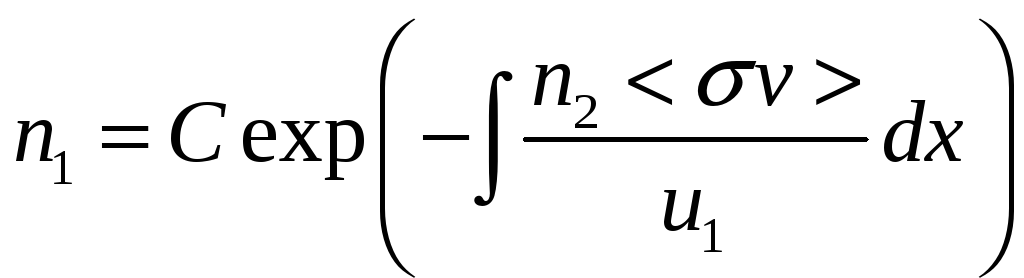
а в случае, когда подынтегральное выражение является константой, то еще проще

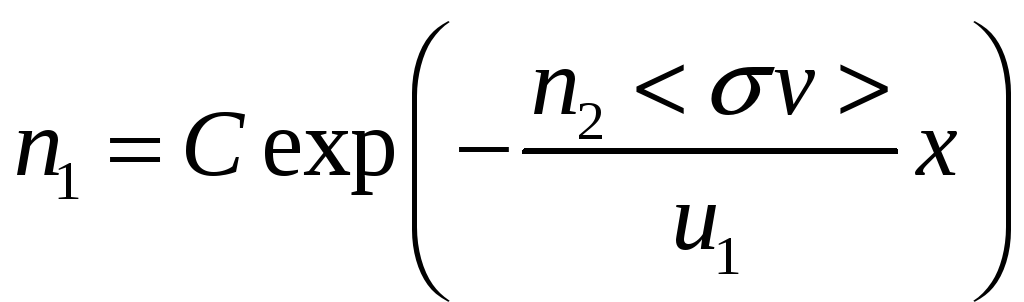
константа находится из граничных условий.

Другой вариант этой же задачи: какова вероятность того, что частица первого вида пролетит расстояние L без каких-либо изменений? Совершенно аналогичным образом получаем ответ (если подынтегральное выражение – константа)

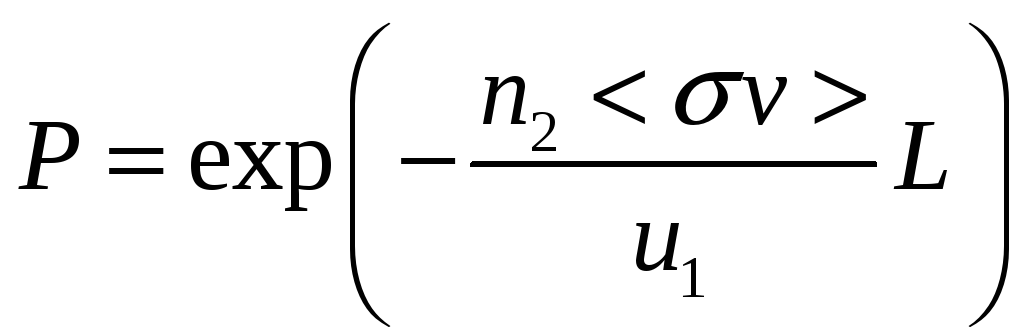
Теперь возвращаемся к методу конечных элементов. Рассмотрим решение дифференциального уравнения

на отрезке [0,1] с граничным условием f(0)=1. Пример реального уравнения такого типа мы только что рассмотрели. Рассмотрим случай с тремя узлами в точках 0, 0.5 и 1. Значение в одном из них задано граничным условием. С учетом этого аппроксимацию функции можно записать следующим образом

при этом имеем следующие определения для пробных функций.

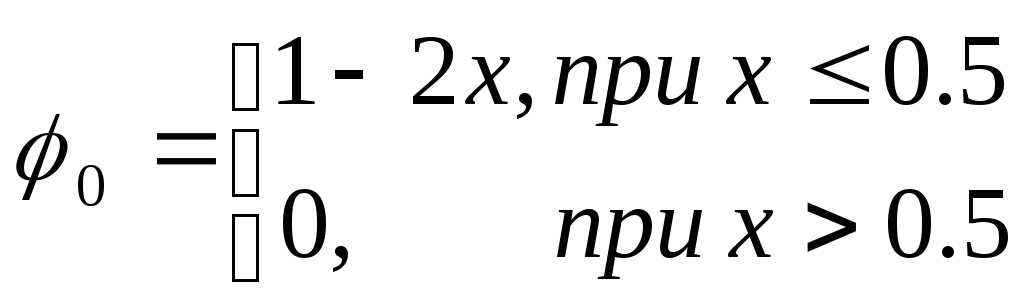
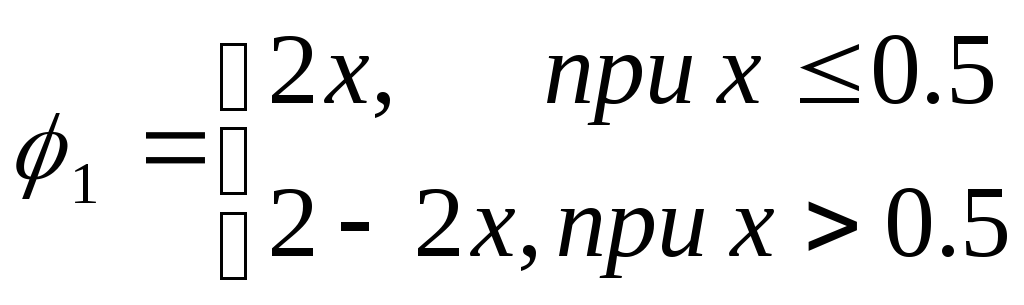
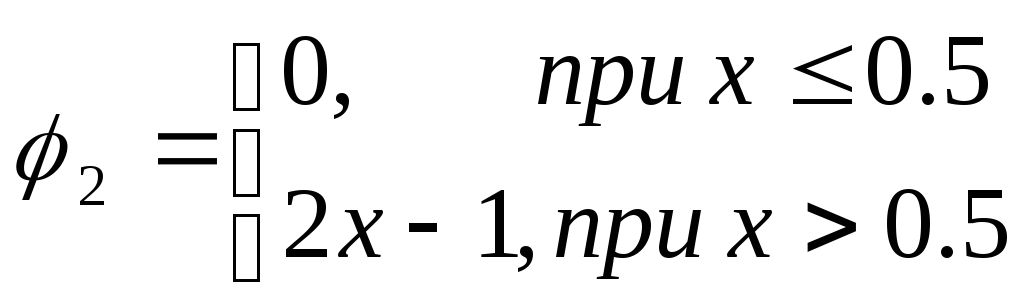
Невязку исходного уравнения можно записать в виде

Уравнения, которые предстоит решить, выглядят так

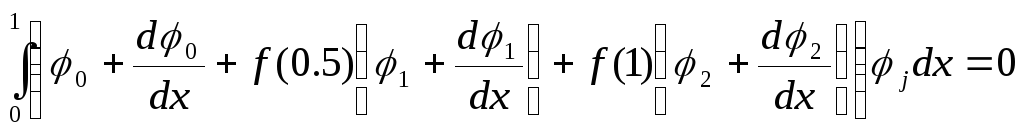
Здесь начинаются преимущества финитных функций, особенно при равных шагах между узлами. Произведение функций, чей индекс отличается более чем на единицу, равно нулю. Это же справедливо и для произведения производной на функцию. Интегралы от ненулевых произведений (при равных шагах между узлами) одинаковы для случаев с одинаковыми разностями индексов. Все эти интегралы можно посчитать один раз и потом всю жизнь пользоваться. Для данного случая (одномерная задача с равномерным шагом) это выглядит так

Нужно учесть, что в крайних узлах могут быть отличия. Если поставлено какое-то граничное условие, то из него и получается уравнение для данного узла. Если граничного условия нет, то нужно помнить, что в крайнем узле интегрирование произведения функции самой на себя или свою производную берется по вдвое меньшему интегралу. Поэтому получаем

В последнем случае знак положителен на правом конце и отрицателен на левом. Теперь спокойно получаем систему уравнений

после упрощений окончательно получаем

решая эту систему получаем

Аналитическое решение того же уравнения дает f(0.5)0.607 и f(1)=0.368.

Зная интегралы от произведений пробных функций, можно рассмотреть общий случай. Так для уравнения вида

для центральных узлов (не граничных) получаем уравнения вида

По сути дела, это тоже разностная схема, только умноженная на шаг. Следовательно, ее можно анализировать теми же методами, какие применяются для метода конечных разностей.

Это все замечательно, но возникает вопрос: как быть, если в исходное уравнение входят вторые производные, а в методе конечных элементов используются линейные аппроксимации? Оказывается, выход есть. Нужно применить один интересный прием. Продемонстрируем его на примере уравнения Пуассона

Невязкой такого уравнения будет

Следовательно, задача сводится к решению уравнений вида

А теперь для первого интеграла применим интегрирование по частям, получим

Первый член в этом соотношении для большинства функций _j равен нулю. Исключение составляют функции равные единице в граничных точках, но там существуют граничные условия, избавляющие нас от необходимости нахождения этого члена. Таким образом, для внутренних узлов необходимо решать уравнения вида

Теперь можно вспомнить, что

и уравнения преобразуются к виду

интегралы от пробных функций известны. Для линейной интерполяции с равномерным шагом они выглядят так (для центральных узлов)

Таким образом, получаем уравнения, которые предстоит решить

Мы получили (с точностью до постоянного множителя) разностную схему, аналогичную получаемой из метода конечных разностей.