1.Понятие функции. Способы задания функций. Примеры. Элементарные функции.

Понятие функции: Х,У-некоторые множества.

Говорят,что заданна функция f,определенная на множестве х,со значениями на множестве У,если каждому элементу x принадлеж.X ставится в соответствии по некоторому правилу,единственный элемент у принадлеж.У.В этом случае Х-область определения,х-аргумент функции,f(x0)-значение функции при значении х=х0.

Способы задания функции:

1.аналитический

2.табличный

3.графический

4.словесный

Примеры.

….

Элементарные функции:

1.у=С ,с-действительное число -const

2.у=х2, αпринадл.R,α =0,степенная функция

3.у=а в х,а >0,а=1,показательная функция

4.у=log ,а>0,а =1,логорифмическая функция

5.у=sinx,у=cosx,у=tg,y=ctg-тригономестрическая

6.у=arcsinx, у=arccosx, y=arctg, y=arccotg

2.Числовая последовательность. Предел числовой последовательности. Примеры.

Если по некоторому закону каждому натуральному числу n поставлено в соответствии вполне определенное число an ,то говорят,что задана числовая последовательность {an}?a1,a2,…an,…,другими словами числовая последовательность –это функция натурального аргумента :an=f(n)

Предел числовой последовательности:

Число а ,называется пределом числовой последовательности {an},если для любого даже сколько угодно малого положительного числа ε>0 найдется такой номер N ,что для всех членов последовательности с номерами n>N верно неравенство |an-A|<ε/

Пример:

…

3.Предел функции. Основные теоремы о пределах. Второй замечательный предел.

Число А называется пределом функции у= f(x) при х ,стремящемся к бесконечности ,если для любого даже сколько угодно малого положительного числа ε>0 найдется такое положительное число S>0,что для всех х,таких что |х|>S,верно неравенство |f(x)-A|<ε

Основные теоремы о пределах.

1)Функция неможет иметь более 1 предела

2) Придел алгебраической суммы конечного числа функции равен такой же сумме пределов этой функции .

3)Предел произведения конечного числа функций= произведению пределов этих функций

4)Придел частного 2х функций = частному предела этих функций, при условии что предел делителя не равен 0

5)Если предел функции f(u) при u-u0=а

6)Если в некоторой окресности х0 ,Х(х)<фи(х),то предел функции Х(х)≤пределу функции фи(х),где х->х0.

Второй замечательный предел имеет вид:

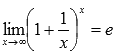
4.Бесконечно малые и бесконечно большие функции .Первый замечательный придел.

-Функция f (x) называется бесконечно малой величиной при х->х0 ,или при х->∞если ее предел равен нулю

-Функция f(x) называется бесконечно большой величиной при х->х0,если для любого даже сколько угодно большого положительного числа М>0 найдется такое положительное число лямда>0,что для всех х,не равных х0 и удолетворяющих условию |х-х0|< лямда ,будет верно неравенство :

|f(x)>M|

Первый замечательный придел.

Первый замечательный предел равен 1 .

5.Предел функции. Неприрывность функции в точке .Точки разрыва функции и их классификация. Примеры.

Число А называется пределом функции f(x) при х ,стремящемся к х0,если для любого даже сколько угодно малого положительного числа ε>0 найдется такое положительное число лямда>0,что для всех х ,не равных х0 и удолетворяющих условию |х-х0|<лямда ,выполняется неравенство :

|f(x)-A|<лямда

Неприрывность функции в точке.

Функция f(x) называется неприрывной в точке х0,если она удолетворяет 3м условиям :

1.определена в точке х0.

2.имеет конечный придел функции при х->х0.

3.этот придел равен значению функции в х0.

Точки разрыва функции и их классификация.

Точка x0 называется точкой разрыва функции f, если функция f не определена в точке x0 или если она определена в этой точке.

Все точки разрыва функции разделяются на:

-точки разрыва первого рода

- второго рода.