1.5. Доверительные интервалы для оценок параметров. Доверительные интервалы прогноза для парной линейной регрессии

Как было отмечено выше, при выполнении предположений первой и второй групп справедливы утверждения:

1) ;

2) .

Следовательно, можно построить доверительные интервалы для параметров и c заданным уровнем доверия, в качестве которого на практике обычно выбирают вероятность 0,95.

Для этого определим по таблице распределения Стьюдента при степенях свободы критическое значение для уровня значимости 0,05, тогда доверительный интервал для параметра с уровнем доверия 0,95 имеет вид

,

где

.

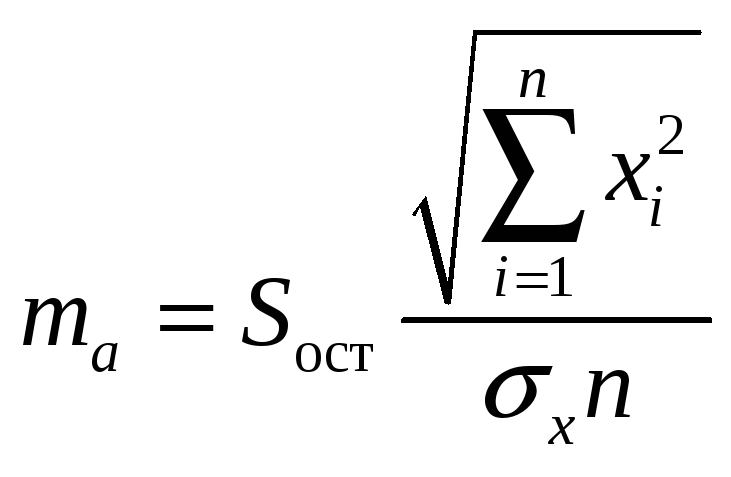Аналогично доверительный интервал для параметра с уровнем доверия 0,95 имеет вид

,

где

.

Точечный прогноз показателя для значения фактора вычисляется по формуле

.

Интервальный прогноз для значения (где ) вычисляется так же, как доверительный интервал для параметров.

Для построения доверительного интервала по таблице распределения Стьюдента при степенях свободы и уровне значимости 0,05 определяется значение . Тогда интервальный прогноз индивидуального значения показателя в точке с уровнем доверия 0,95 дается неравенством

,

где

.

Оценка средней относительной ошибки аппроксимации (т.е. модуля среднего отклонения расчетных значений от фактических) производится по формуле

.

1.6. Метод Гольдфельда—Квандта проверки гипотезы гомоскедастичности

Среди основных предположений регрессионного анализа важную роль играет предположение гомоскедастичности, которое заключается в равенстве дисперсий наблюдений:

Нарушение этого предположения сильно ухудшает качество оценок неизвестных параметров.

Возможны различные нарушения этого предположения в рамках парной регрессии. Одно из распространенных нарушений связано с тем, что дисперсия наблюдений может возрастать вместе с ростом значения фактора (объясняющей переменной):

,

при этом .

Это нарушение гомоскедастичности может быть обнаружение с помощью критерия Гольдфельда—Квандта.

Кратко критерий можно описать следующим образом:

1) упорядочим выборку , по возрастанию объясняющей переменной так, чтобы ;

2) исключим центральных наблюдений, в результате чего получим две выборки, состоящие из наблюдений: первая выборка содержит наблюдения с небольшими значениями объясняющей переменной: , вторая выборка содержит наблюдения с большими значениями объясняющей переменной ;

3) Построим две парные линейные регрессии по полученным выборкам и вычислим остаточные суммы квадратов по каждой из выборок: для первой выборки и для второй выборки;

4) вычислим статистику . Если верна гипотеза гомоскедастичности , то статистика имеет распределение Фишера с степенями свободы;

5) по таблице распределения Фишера при степенях свободы и уровне значимости 5% определяется значение . Тогда:

1. если , то гипотеза гомоскедастичности 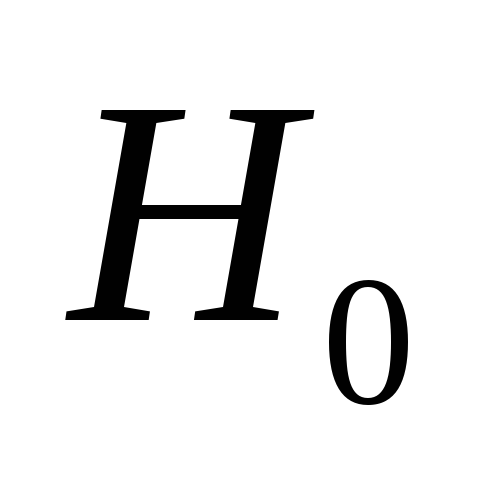отклоняется;

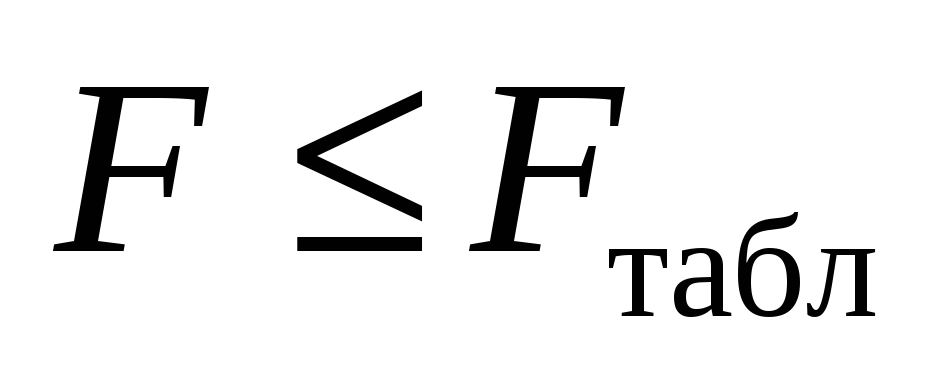2. Если , то гипотеза гомоскедастичности принимается.

2. Множественная регрессия

2.1. Спецификация модели

В отличие от случая парной регрессии при построении множественной регрессии предполагают, что имеется несколько объясняющих факторов.

Пусть — изучаемый эконометрический показатель, — объясняющие факторы.

Примеры:

1) Показатель — расходы фирмы за месяц, факторы: — объем выпущенной продукции за месяц, — стоимость ресурсов (электроэнергии и т.п.) в этом месяце.

2) Показатель — спрос на товар, факторы: — цена единицы товара, — цена товаров-заменителей.

Гипотетическая эконометрическая модель, приводящая к множественной регрессии, имеет следующий вид:

где — неизвестная функциональная зависимость, — случайное слагаемое, представляющее собой совокупное действие не включенных в модель факторов.

Основная задача эконометрического исследования — построение эмпирической модели (множественной регрессии) следующего вида:

,

где — эмпирическая зависимость (регрессия), «наилучшим» способом описывающая усредненную зависимость между изучаемым показателем и объясняющими факторами. После построения регрессии необходима последующая верификация модели (проверка статистической значимости построенной множественной регрессии).

Экспериментальная основа построения эмпирической регрессии — многомерная выборка

,

где — объем выборки (объем массива экспериментальных данных).

Аналогично случаю парной регрессии основная задача спецификации модели заключается в выборе функциональной зависимости. Основные методы выбора функциональной зависимости в основном те же, что и в случае парной регрессии. Однако задача выбора функциональной зависимости для множественной регрессии оказывается принципиально более сложной, чем в случае парной регрессии. Причина заключается в многомерной природе объясняющих переменных.

Применяя аналитический метод, в примере 1, аналогично случаю парной регрессии, нетрудно получить следующую модель:

,

где — условно-постоянные расходы, — условно-переменные расходы.