40. Явище змочення. Капілярні явища.

Якщо взаємодія молекул рідини менша, ніж їх взаємодія з молекулами контактного твердого тіла, то маємо випадок змочування і навпаки, коли ця взаємодія більша - незмочування. Інтенсивність змочування характеризується кутом змочування Q, який утворюється між дотичною до поверхні рідини і поверхнею твердого тіла. Відлік кута виконують у бік рідини. Якщо - поверхня тіла змочувана, а якщо - незмочувана.Явища змочування і незмочування відіграють важливе значення в побуті і техніці, якби вода не змочувала тіло людини, то марним було б купання. Добре змочування потрібне під час фарбування і прання, паяння, збагачення руд цінних порід та інших технічних процесів.Явище змочування і незмочування виявляється у піднятті і спусканні рідини в тонких трубках (капілярах). Розглянемо капілярні явища.Підняття рідини в капілярі припиниться тоді, коли сила тяжіння піднятого стовпа рідини зрівноважить силу поверхневого натягу:F_пов = F_тяж.Сила поверхневого натягу F_пов = 2prs. Сила тяжіння F_т = mg. Оскільки m = rV = rpr² h, рівність (4) набуде вигляду:2prs = rpr²hg.  Із рівності знаходимо висоту підняття рідини для циліндричного капіляра:де h - висота підняття рідини в циліндричному капілярі; s - коефіцієнт поверхневого натягу рідини; r - густина рідини; r - радіус капіляра; g - прискорення вільного падіння.Капілярні явища мають велике значення в природі і техніці. Завдяки цим явищам відбувається проникнення вологи з ґрунту в стебла і листя рослин. Саме в капілярах відбуваються основні процеси, пов'язані з диханням і живленням організмів. У тілі дорослої людини приблизно 160·10⁹ капілярів, загальна довжина яких сягає 60 - 80 тис. км. У будівництві враховують можливість підняття вологи по капілярних порах будівельних матеріалів. Для захисту фундаменту і стін від дії ґрунтових вод та вологи застосовують гідроізоляційні матеріали: толь, смоли тощо.Завдяки капілярному підняттю вдається фарбувати тканини.Часто капілярні явища використовують і в побуті. Застосування рушників, серветок, гігроскопічної вати, марлі, промокального паперу можливе завдяки наявності в них капілярів.

40. Кристалічні та аморфні тіла. Типи кристалічних решіток.

Кристалічні тіла мають певну температуру плавлення, незмінну при сталому тиску; в’язкість аморфних речовин під час нагрівання зменшується; вони переходять у рідкий стан, розм’якшуючись поступово.Кристали характеризуються наявністю значних сил міжмолекулярної взаємодії і зберігають сталим не лише свій об’єм, а й форму. Правильна геометрична форма є істотною зовнішньою ознакою будь-якого кристала в природних умовах. Розглядаючи окремі кристали, можна переконатися, що вони обмежені плоскими, ніби шліфованими гранями у вигляді правильних багатокутників.Кристали певної речовини можуть мати різну форму, оскільки вона залежить від умов їх утворення. Монокристали і полікристали. Іноді весь шматок твердої речовини може становити собою один кристал. Такі, наприклад, шматочки цукру, солі, гірського кришталю тощо. Це все окремі кристали, їх називають монокристалами. В інших випадках тіла складаються з безлічі кристалів, які зрослися між собою. Кристалічну будову мають всі метали у твердому стані. Тіло, яке складається з безлічі невпорядковано розміщених дрібних кристалів називають полікристалічним, або полікристалом. Полікристалічні тіла є ізотропними, тобто їх фізичні властивості, як і аморфних тіл, у всіх напрямках однакові. Це пояснюється тим, що полікристали складають з величезної кількості невпорядковано орієнтованих дрібних кристаликів, які зрослися між собою.Широке застосування в сучасній фізиці і техніці дістали монокристали. Майже всі напівпровідникові прилади – це монокристали зі спеціально введеними домішками, які надають їм тих чи інших властивостей.Внутрішня будова кристалів. Залежність фізичних властивостей кристалів від напряму і правильність їхніх геометричних форм давали підстави для припущення про впорядкованість частинок, які утворюють кристал. Частинки, з яких складається кристал, при тепловому русі коливаються навколо положень рівноваги, які називають вузлами.Інші кристали мають складнішу будову. В їхніх вузлах містяться атоми вуглецю. Вузол – це положення рівноваги частинки, яка входить до складу кристала, тобто точка. Відстань між вузлами умовно позначає відстань між центрами атомів і молекул.Розрізняють чотири типи кристалів (і кристалічних решіток): іонні, атомні, металічні і молекулярні.Іонні кристали. У вузлах решітки іонних кристалів знаходяться позитивно і негативно заряджені іони. Сили взаємодії між ними в основному електростатичні.Атомні кристали. Їхні кристалічні решітки утворюються внаслідок щільної упаковки атомів, найчастіше однакових (під час взаємодії однакових атомів іони не утворюються. Атоми, що знаходяться у вузлах, зв’язані із своїми найближчими сусідами ковалентним зв’язком.За умови ковалентного зв’язку електрони не переходять від одного атома до іншого (іони не утворюються), а виникає одна чи кілька спільних електронних пар.Молекулярні кристали. У вузлах їх кристалічної решітки знаходяться молекули речовини, зв’язок між якими забезпечується силами молекулярної взаємодії. Металічні кристали. У всіх вузлах гратки металічних кристалів розміщені позитивні іони металу. Між ними хаотично, подібно до молекул газу, рухаються електрони, які відокремилися від атомів під час кристалізації металу. Разом з тим і електрони утримуються іонами в її межах. Наявність вільних електронів у металі забезпечує добру електропровідність і теплопровідність цих речовин.Кожна частинка в кристалі (молекула, атом чи іон) знаходиться в певному положенні рівноваги, в якому сили відштовхування і притягання з боку інших частинок, які утворюють кристал, однакові.Спостерігати і безпосередньо вимірювати сили, які діють на окремі молекули, атоми чи іони, не можна.Щодо деформації тіл. При малих деформаціях напруга σ прямо пропорційна відносному видовженню ε. У формулі закону Гука: σ = εЕ.

Властивість твердих тіл (або матеріалів, з яких вони виготовлені) відновлювати свою форму і об’єм після припинення дії сили називають пружністю.Деформацію, яку має тіло після припинення дії сили, називають залишковою. Найбільше навантаження, яке витримує зразок перед розриванням, називають навантаженням межі міцності, а напругу, яка відповідає цьому максимальному навантаженню, - межею міцності.На пружність і пластичність тіл істотно впливає температура.Однією з найважливіших механічних характеристик матеріалів є їхня міцність, тому в основному саме завдяки їй стають надійними різні споруди і машини. Під міцністю розуміють здатність матеріалу опиратися руйнуванню і залишковій деформації, які виникають внаслідок зовнішніх впливів.На відміну від кристалічних аморфні тіла повністю ізотропні, тобто їх властивості однакові в усіх напрямах. Аморфні тіла не мають певної температури плавлення. Якщо, наприклад, нагрівати скло, воно стає м’яким і тягучим. Друга їх характерна властивість – пластичність. Таким чином, залежно від характеру впливу (зокрема часу, протягом якого діє сила) аморфні речовини поводять себе або як крихкі тверді тіла, або як дуже в’язкі рідини.Аморфний стан речовини нестійкий: через певний час аморфна речовина переходить у кристалічну.

43. Закон Дюлонга-Пті визначає питому теплоємність твердого тіла за формулою

де c - питома теплоємність, R - універсальна газова стала, M - молярна маса.

Закон Дюлонга-Пті можна переписати для теплоємності твердого тіла у вигляді:

,де С - теплоємність, k_B - стала Больцмана, N - число атомів у кристалі.

Для справедливості закону Дюлонга-Пті необхідно, щоб енергії теплового руху вистачало для збудження всіх можливих типів коливань у твердому тілі. При низьких температурах деякі з коливань не збуджуються. Це явище зумовлене законами квантової статистики (в даному випадку - статистики Бозе-Ейнштейна). Тому при низьких температурах закон Дюлонга-Пті не діє.

44.Однокомпонентні системи.  Якщо система складається тільки з одного компонента, тобто являє собою чисту індивідуальну речовину, те можливість одночасного існування всіх трьох фаз - твердої, рідкої і газоподібної, за правилом фаз визначається відсутністю ступенів свободи, тому що в цьому випадку: С=1-3+2=0  і система безваріантна. Така система може існувати тільки при строго визначених значеннях температури і тиску (для води t=0,0075°С и р=4,579 мм рт. ст.). Зміна шкірного з цих розумів приводити до зникнення однієї з фаз і система стає двохфазною.

двофазна система-рідина і насичена пари. У цьому випадку:  С=1-2+2=1  і система є одноваріантною. Отже, не порушуючи фазової рівноваги, можна довільно змінювати або температуру або тиск. 

У таких системах строго однозначна залежність між температурою і тиском насиченої парі. при зміні температури парі буде о змінюватися тиск і, навпаки. крива тиску водяної парі (мал.1). 

При будь-якому рівноважному переході речовини з однієї фази в іншу дотримується залежність, що виражається рівнянням Клаузіуса — Клапейрона 

   де r — теплота фазового переходe (випаровування, плавлення, сублімації і ін.) у ккал/кг·мол;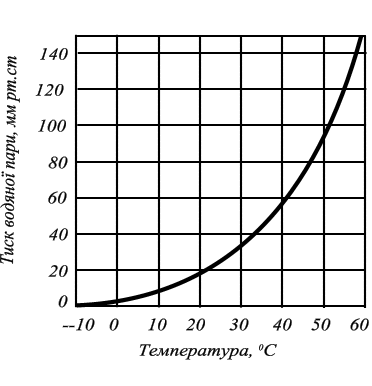

— тепловий еквівалент роботи в ккал/кгс; 

Т — абсолютна температура фазового переходу в °К; 

Р — тиск у кгс/м²;  — зміна мольного об’єму речовини при фазовому переході в м³/кг·мол.  Рис.1. Крива тиску насиченої водяної пари.  Стосовно до двохфазної системи рідина — пара перепишемо це рівняння так:

  де r – теплота випаровування при даній температурі в ккал1кг·мол;

V_п — молярний об’єм пари в м³/кг·мол; 

V_ж — молярний об’єм рідини в м^а/кг-мол

. В області невисоких тисків пари молярний об’єм рідини дуже малий у порівнянні з молярним об’ємом пари, тому

без великої похибки можна величиною V_ж знехтувати, приймаючи V_ж=0. Тоді  де R=1,99 ккал/кг·мол·°К.

 При цих умовах рівняння приймає наступний вид: 

або  або  При невеликих інтервалах температур величина r має приблизно постійне значення. Тоді інтегрування рівняння дає  де C – стала інтегрування. 

По цьому рівнянню зручно вести практичні розрахунки, тому що воно є рівнянням прямої залежності логарифма тиску від зворотньої величини абсолютної температури. Якщо для якої-небудь однієї температури Т відомий тиск Р, то, знаючи величину r, можна з знайти числове значення константи C, після чого побудувати пряму в координатах lgP,  і по ній знаходити значення Р для будь-яких інших температур.  Якщо величина r також невідома, те для побудови діаграми необхідно знати тиски при двох температурах, скласти два рівняння і, вирішуючи їх, визначити значення r і С. 

Рівняння можна інтегрувати в межах від T₁ до Т₂ і відповідно від Р₁ до Р_2, тоді одержимо нове рівняння для визначення тиску насичених парів в залежності від температури:

.

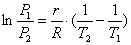Потрі́йна то́чка — точка на фазовій діаграмі, при якій можуть співіснувати у рівновазі тверда, рідка й газова фаза однієї речовини.

Для води потрійна точка реалізується при температурі 0.01 ^oC і тиску 611.73 Па .

За правилом фаз для однокомпонентної термодинамічної системи потрійна точка єдина.

45. Клапейрона — Клаузіуса рівняння, термодинамічне рівняння, що відноситься до процесів переходу речовини з однієї фази в іншу (випар, плавлення, сублімація, поліморфне перетворення і ін.). Згідно До. — До. в., теплота фазового переходу(наприклад, теплота випару, теплота плавлення) при рівноважно протікаючому процесі визначається вираженням

КЛАПЕЙРОНА-КЛАУЗІУСА РІВНЯННЯ

• диференціальне рівняння, яке встановлює зв'язок між тиском р і абс. температурою Т чистої речовини у станах, що відповідають фазовим переходам 1-го роду (випаровуванню, сублімації, плавленню тощо). Має вигляд;

де r — питома теплота фазового переходу, ∆V — різниця питомих об'ємів фаз. Рівняння вивів Б. П. Е. Клапейрон (1834) і обгрунтував Р. Клаузіус (1850).