2. Построение совершенных нормальных форм

Для записи функции, заданной таблицей истинности, в виде формулы вводится параметризация, позволяющая охарактеризовать значение переменной в «энке». Пусть , где  – параметр, равный нулю или единице, и характеризующий значение переменной х на наборе. Таким образом, 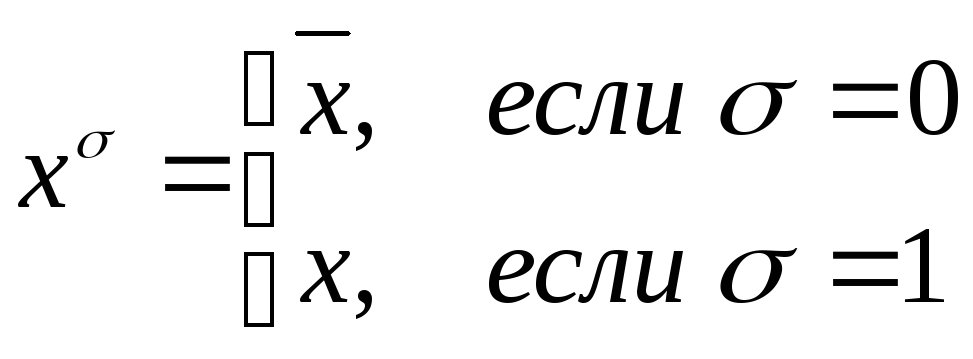. Т.е. если на наборе значение переменной х равно 0, то пишут «», а в случае, когда соответствующее значение равно 1, то записывают просто «х». Заметим, что х^=1 тогда и только тогда, когда х=.

Выражение вида называется совершенной дизъюнктивной нормальной формой (СДНФ). Из этого определения следует, что для построения СДНФ в таблице истинности функции f надо рассматривать лишь те строки, где функция равна единице. Для каждой такой строки записывается элементарная конъюнкция, состоящая из всех переменных функции. При этом переменная входит в конъюнкцию с отрицанием, если в рассматриваемой строке её значение равно нулю, и без отрицания – в противном случае.

Выражение вида называется совершенной конъюнктивной нормальной формой (СКНФ). Из этого определения следует, что для построения СКНФ в таблице истинности функции f надо рассматривать лишь те строки, где функция равна нулю. Для каждой такой строки записывается элементарная дизъюнкция, состоящая из всех переменных функции. При этом переменная входит в дизъюнкцию с отрицанием, если в рассматриваемой строке её значение равно единице, и без отрицания – в противном случае.

Для каждой функции алгебры логики СДНФ и СКНФ записывается единственным образом.

Примеры построения СДНФ и СКНФ.

x	у	f(x,у)	СДНФ	СКНФ
0	0	1
0	1	1
1	0	0
1	1	1	x & y
Таблица 6

В таблице 6 в столбце СДНФ показаны элементарные конъюнкции в единичных строках функции, а в столбце СКНФ – элементарная дизъюнкция в строке, где функция равна нулю. Тем самым, СДНФ=    x & y, СКНФ =. Эти формулы эквивалентны между собой и эквивалентны формуле (ху).

x	у	f(x,у)	СДНФ	СКНФ
0	0	1
0	1	0
1	0	0
1	1	1	x & y
Таблица 7

В таблице 7 в столбце СДНФ показаны элементарные конъюнкции в единичных строках функции, а столбце СКНФ – элементарные дизъюнкции в нулевых строках. Тем самым, СДНФ=  x & y, СКНФ = ()&(). Эти формулы эквивалентны между собой и эквивалентны формуле (ху).

Если функция задана формулой, то для построения её СДНФ или СКНФ применяют эквивалентные преобразования заданной формулы.

Пусть функция представлена формулой со связками {, &, }. Тогда для преобразования формулы в совершенную дизъюнктивную нормальную форму необходимо вначале представить формулу в виде – логической суммы логических произведений. Этого можно добиться с помощью законов дистрибутивности или других тождеств. Затем добавить к каждой элементарной конъюнкции (каждому логическому произведению переменных) единичные множители, составленные по закону исключенного третьего из символов тех переменных, которых недостает в данной конъюнкции до полного набора переменных, и далее выполнить преобразования, раскрывая скобки и приводя «подобные члены» по закону идемпотентности.

Например, f(x,y,z)=. Первое слагаемое в формуле преобразуем по закону Де Моргана, во втором слагаемом раскроем скобки с помощью закона дистрибутивности и поменяем местами сомножители, используя закон коммутативности. Тогда f(x,y,z)= – это выражение имеет требуемую форму: логическая сумма логических произведений переменных или их отрицаний, такая форма называется также дизъюнктивной нормальной формой (ДНФ). Теперь к каждой элементарной конъюнкции в ДНФ добавим единичный множитель: к первой –, ко второй – и к третьей . Получим:

f(x,y,z)==

=. Теперь приведем «подобные члены»: . Полученное выражение и есть СДНФ данной функции.

Для представления функции в виде совершенной конъюнктивной нормальной формы необходимо вначале представить её в виде произвольной конъюнктивной нормальной формы (КНФ) – это выражение вида (логическое произведение логических сумм переменных или их отрицаний, или конъюнкция элементарных дизъюнкций). Этого можно добиться с помощью приведенных выше законов. Затем в каждую элементарную дизъюнкцию добавить нулевые слагаемые, составленные по закону противоречия из недостающих ей до полного набора переменных. Далее выполнить преобразования, применяя законы дистрибутивности, коммутативности и идемпотентности.

Например, . Приведем к виду КНФ:

f(x,y,z)=. В этом выражении 4 элементарных дизъюнкции, причем в первой из них не хватает до полного набора переменных y и z, во второй – переменной z, в третьей – х и в четвертой – у. Добавим их в виде нулевых слагаемых, пользуясь законом противоречия. Тогда f(x,y,z)==

=

. Теперь воспользуемся законами идемпотентности и коммутативности и получим СКНФ(f(x,y,z))=

=

Выражение вида , где s  n и суммирование выполняется по модулю 2 и проводится по всевозможным подмножествам номеров переменных, называется полиномом Жегалкина или совершенной полиномиальной нормальной формой (СПНФ). Здесь – коэффициент, равный нулю или единице, и стоящий перед произведением переменных с номерами: i₁, i₂,…, i_s. Важно, что представление в виде СПНФ для каждой функции алгебры логики единственно.

Примеры:

1) Построим полином Жегалкина для элементарной функции f(x,y) = х  у. Сначала запишем его в общем виде: f(x,y) =. Где a, b, c и d – неопределенные коэффициенты, значения которых будут найдены путем подстановки различных комбинаций значений переменных х и у в выражение общего вида. Итак, f(0,0) = 0 =. Отсюда d=0.

f(0,1) = 1 =. Отсюда с=1.

f(1,0) = 1 =. Отсюда b=1.

f(1,1) = 1 =. Отсюда a=1.

Тем самым, при подстановке найденных значений коэффициентов в выражение общего вида, получим: (х  у) =.

2) Построим полином Жегалкина для элементарной функции f(x,y) = х  у. Запишем выражение общего вида: f(x,y) = и найдем коэффициенты: f(0,0) = 1 =. Отсюда d=1.

f(0,1) = 0 =. Отсюда с=1.

f(1,0) = 0 =. Отсюда b=1.

f(1,1) = 1 =. Отсюда a=0.

И полином Жегалкина: (х  у) = х  у  1

Рассмотренный в примерах способ построения полинома Жегалкина представляет собой так называемый метод неопределенных коэффициентов.

Ввиду важности полиномиального разложения функций алгебры логики укажем и на другие способы получения этого разложения.

Если функция задана формулой со связками {Ø,&,Ú}, то для перехода к полиному Жегалкина необходимо воспользоваться тождествами: _, х&у = х·у, (х Ú у) =.

Например, пусть f(x,y,z) = .

Тогда  f(x,y,z) = ((x1)·(y1)  y)  (z 1) = = ((x1)·(y1)·y  (x1)·(y1)  y)  (z 1) =

=((x1)·(y1)·y  (x1)·(y1)  y)·(z 1)  ((x1)·(y1)·y  (x1)·(y1)  y) (z 1) =((х·уxy1)·y  х·уxy1y)·(z 1)  (х·уxy1)·y  х·уxy1y  z1 = (воспользуемся тем, что х·х=х и xх=0) = (х·уx1)·(z 1)  х·у  x  z = х·у·z  х·z  z  х·у  x  1 х·у  x  z = = х·у·z  х·z  1

Если функция задана таблицей, то для получения её полинома Жегалкина вначале следует записать СДНФ, затем в полученном выражении заменить все конъюнкции умножением, дизъюнкции – сложением по модулю два, а отрицания – сложением с единицей. Далее раскрыть скобки и применить тождества х·х=х и xх=0.

Например, пусть столбец значений функции f(x,y,z) в таблице истинности равен (1, 1, 1, 1, 1, 0, 1, 1). Запишем совершенную дизъюнктивную нормальную форму для этой функции: СДНФ(f(x,y,z)) = . Теперь выполним указанные выше замены:

f(x,y,z)=(х1)(уÅ1)(zÅ1) Å (xÅ1)(yÅ1)z Å (xÅ1)y(zÅ1) Å (xÅ1)yz Å  x(yÅ1)(zÅ1) Å xy(zÅ1) Å xyz, и раскроем скобки: (xyz Å xy Å xz Å yz Å x Å y Å z Å1) Å (xyz Å xz Å yz Å z) Å (xyz Å xy Å yz Åy)Å (xyz Å yz) Å (xyz Å xy Å xz Å x) Å (xyz Å xy) Å xyz = х·у·z  х·z  1