- •Программа по курсу «Дискретная математика» для заочной формы обучения
- •Методика рецензирования контрольной работы.
- •Краткие теоретические сведения
- •Множества и операции над ними
- •Бинарные отношения
- •Отношение эквивалентности
- •Отношение упорядоченности
- •Функции
- •Функции и формулы алгебры логики
- •Двойственные функции и совершенные нормальные формы
- •Принцип двойственности
- •Построение совершенных нормальных форм
- •Полнота и замкнутость систем функций алгебры логики
- •Полные системы функций алгебры логики
- •Важнейшие замкнутые классы
- •Задание к контрольной работе по дискретной математике
- •I. Множества и операции над ними.
- •Варианты контрольных работ Вариант №1
- •Вариант №2
- •Вариант №3
- •Вариант №4
- •Вариант №5
- •Вариант №6
- •Вариант №7
- •Вариант №8
- •Вариант №9
- •Вариант №10
- •Вариант №11
- •Вариант №12
- •Вариант №13
- •Вариант №14
- •Вариант №15
- •Вариант №16
- •Вариант №17
- •Вариант №18
- •Вариант №19
- •Вариант №20
- •Вариант №21
- •Вариант №22
- •Вариант №23
- •Вариант №24
- •Вариант №25
- •Пример решения контрольной работы
- •Список литературы
- •400131, Волгоград, просп. Им. В.И. Ленина, 28
- •400131, Волгоград, ул. Советская, 35
-
Функции
Бинарное отношение Р называется однозначным, если для всякого элемента xпр1Р существует не более одного (а может быть и вовсе ни одного) значения yпр2Р.
Всюду определенное и однозначное бинарное отношение fAB называется функцией или отображением множества А в множество В. Если А и В числовые множества, то функция называется числовой.
Для отображений чаще
используются обозначения вида: f :
или ![]() .
Пару (х, у) f
чаще обозначают y = f(x), и
поскольку отображение – это частный
случай бинарных отношений, то определены
все ранее введенные понятия: образа и
прообраза для элементов и множеств,
области определения и области значений
отображения (или функции), а также
понятия композиции отображений и
обратного отображения.
.
Пару (х, у) f
чаще обозначают y = f(x), и
поскольку отображение – это частный
случай бинарных отношений, то определены
все ранее введенные понятия: образа и
прообраза для элементов и множеств,
области определения и области значений
отображения (или функции), а также
понятия композиции отображений и
обратного отображения.
Отображение (функция) называется постоянным, если х х следует f(x1) = f(x2). Элемент х называется неподвижной точкой отображения, если f(x) = x.
Отображение f : AB называется инъективным или взаимно-однозначным отображением множества А в В, если для х х f(x1) f(x2). Т.е. каждый образ имеет только один прообраз. Подчеркнем, что не все элементы множества В обязаны иметь прообраз (должны быть чьими-нибудь образами).
Отображение называется сюрьективным (или сюрьекцией или отображением множества А на множество В), если f(A) = B или yB xA (один или несколько) и y=f(x), т.е. все элементы множества В являются чьими-нибудь образами (имеют по крайней мере один прообраз).
Отображение называется биективным (биекцией или взаимно однозначным отображением A на B), если оно одновременно инъективно и сюрьективно.
Биективное отображение A на А называется тождественным отображением, если все его элементы являются неподвижными точками, т.е. xA следует, что f(x) = x.
Утверждения:
1) Если f : AВ и g : ВС – две функции, то g ∘ f: A→C – тоже является функцией.
2) Пусть f : AВ – функция. Для того, чтобы f ‑1: ВА было функцией, необходимо и достаточно, чтобы f было биективным отображением. В этом случае f –1 называется отображением, обратным к f, или обратной функцией. При этом f ‑1 – также биективно, f ‑1∘ f =IA – тождественное отображение А и f ∘ f ‑1 =IB – тождественное отображение В.
Отображение f : AВ называется обратимым слева (справа), если существует отображение fЛ‑1: ВА ( fП‑1: ВА ) такое, что f Л‑1∘ f =IA ( f ∘ f П‑1 =IB ).
Критерий обратимости слева (справа)
Для того, чтобы отображение f : AВ было обратимым слева (справа), необходимо и достаточно чтобы оно было инъективным (сюрьективным).
-
Функции и формулы алгебры логики
Алгебра логики задается двумя множествами: U и Р2, где U – это множество всех высказываний, принимающих значения «истина» или «ложь», или любое другое множество, элементы которого могут принимать одно их двух значений или находиться в одном из двух состояний. Например, множество переключателей, каждый из которых может быть «включен» или «выключен», или множество электрических сигналов, поступающих на вход некоторого устройства, – «сигнал есть» или «сигнала нет» и т.п.. Сопоставим значению «истина» символ «1», а значению «ложь» – символ «0». Таким образом, алгебра логики оперирует на множестве всех высказываний со значениями из двухэлементного множества Е2 ={0, 1}.
Множество Р2 –
это множество всех таких функций,
которые принимают «истинностные»
значения 0 или 1, если их аргументы
пробегают те же значения. Т.е., если
f(x1,x2,…,xn)
– истинностная функция от n
аргументов или f(x1,x2,…,xn)Р2,
то она определяет отображение f:
![]() ® E2.
Алгебра логики занимается изучением
свойств этих функций.
® E2.
Алгебра логики занимается изучением
свойств этих функций.
Истинностные функции называют также функциями алгебры логики, или булевыми функциями, или переключательными функциями.
Число всех функций алгебры логики от n переменных равно 22n.
Функции алгебры логики могут быть заданы одним из следующих способов: 1) словесное описание;
-
табличное представление;
-
графическое изображение;
-
алгебраическое (в виде формулы).
Таблица значений функции алгебры логики называется таблицей истинности или комбинационной таблицей.
Ниже приведены таблицы истинности элементарных функций алгебры логики, к которым относятся функции от одной и от двух переменных.
|
x |
g1(x) |
g2(x) |
g3(x) |
g4(x) |
|
|
0 |
0 |
0 |
1 |
1 |
|
|
1 |
0 |
1 |
0 |
1 |
Таблица 1 |
В таблице 1 функция g1(x) – это константа ноль или «противоречие».
Функция g2(x) – «тождественная функция x».
Функция g3(x)
– «отрицание x»,
обозначается «![]() »
или «
»
или «![]() ».
».
Функция g4(x) – константа единица или «тавтология».
|
x |
y |
f1 |
f2 |
f3 |
f4 |
f5 |
f6 |
f7 |
f8 |
f9 |
f10 |
f11 |
f12 |
f13 |
f14 |
f15 |
f16 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
|
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
|
Обозначение |
0 |
& |
|
x |
|
y |
|
|
|
|
|
yx |
|
xy |
| |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 2 |
||
В таблице 2 приведены также обозначения элементарных функций. Эти обозначения (символы) принято называть пропозициональными связками или символами логических операций.
Функция f1(x,y) – это так же, как и в таблице 1, константа ноль или «противоречие».
Функция f2(x,y)=x&y – «конъюнкция» х и у или «логическое умножение». Читается: «х и у». Значения этой функции можно получить простым умножением значений её аргументов или как наименьшее из значений аргументов, т.е. f2(x,y) = x&y = xy = min(x, y).
Функции f3(x,y)=
![]() и f5(x,y)=
и f5(x,y)=
![]() –
это «условное вычитание» у из
х, и х из у, соответственно.
Их значения можно получить по правилу:
–
это «условное вычитание» у из
х, и х из у, соответственно.
Их значения можно получить по правилу:
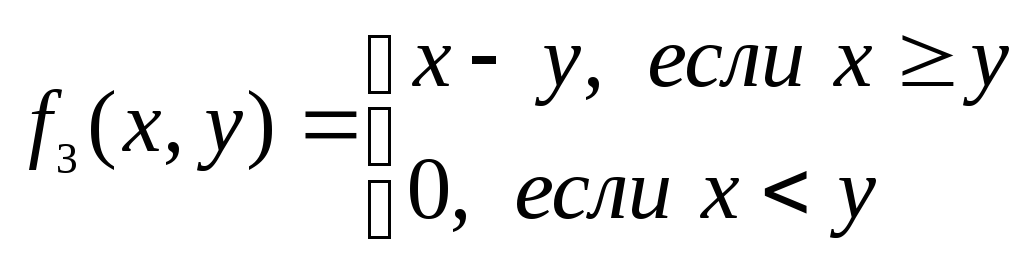 и
и
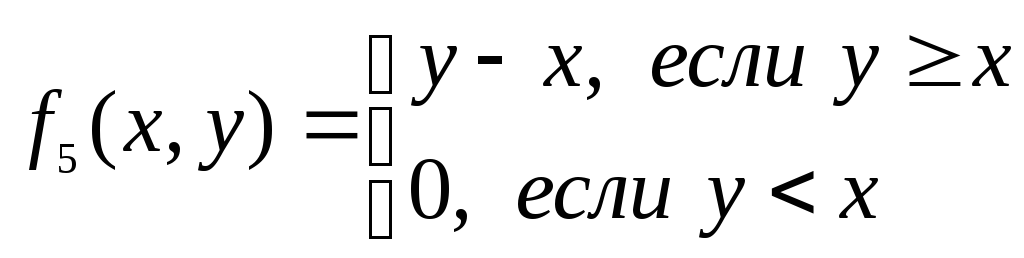 .
.
Функции f4(x,y)=х и f6(x,y)=у – как и в таблице 1, «тождественная функция x» и «тождественная функция у» соответственно.
Функция f7(x,y)=ху – «сложение по модулю 2» или «исключающее или». Значения этой функции равны остатку от деления на 2 суммы её аргументов.
Функция f8(x,y)=ху – «дизъюнкция» х и у или «логическое сложение». Читается: «х или у». Значения этой функции можно получить как наибольшее из значений аргументов, т.е. f2(x,y) = xy = max(x, y).
Функция f9(x,y)=ху – «стрелка Пирса» или «отрицание дизъюнкции» или «конъюнкция отрицаний». Последние два названия обусловлены правилом, по которому получаются значения этой функции.
Функция f10(x,y)=ху
– «эквиваленция». Читается: «х
эквивалентно у». Значения этой
функции получаются по правилу:
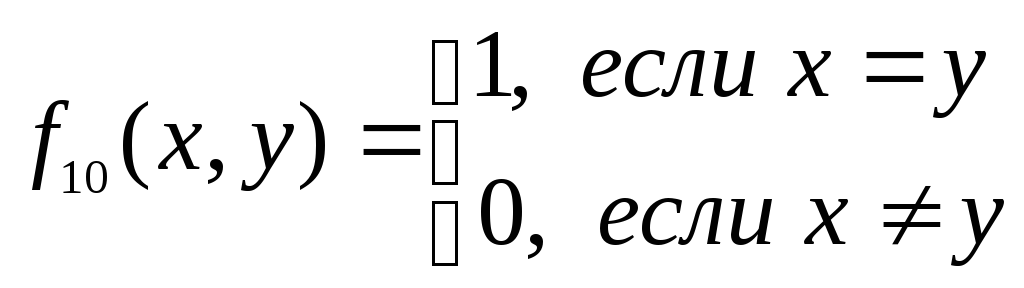 .
.
Функции f11(x,y)=
![]() и f13(x,y)=
и f13(x,y)=
![]() – это так же, как и в таблице 2, «отрицание
у» и «отрицание х» соответственно.
– это так же, как и в таблице 2, «отрицание
у» и «отрицание х» соответственно.
Функции f12(x,y)= yx и f14(x,y)= xy – это так называемая «импликация». Для чтения выражения xy можно использовать фразу «х влечет у» или «если х, то у». Значения xy получаются как ответ на вопрос «х меньше, либо равно у?». При этом положительный ответ записывается «1», а отрицательный – «0».
Функция f15(x,y)= y | x – «штрих Шеффера» или «отрицание конъюнкции» или «дизъюнкция отрицаний». Последние два названия обусловлены правилом, по которому получаются значения этой функции.
Последняя функция в таблице 2 – это так же, как и в таблице 1, константа единица или тавтология.
Из пропозициональных переменных, элементарных функций и скобок строятся логические формулы.
Вычисление значений формулы выполняется путем подстановки различных наборов значений переменных, входящих в формулу. Результаты вычислений обычно оформляются в виде таблицы истинности формулы. Такие таблицы могут быть полными и сокращенными.
Для построения полной таблицы истинности исходную формулу разделяют на подформулы и затем вычисляют значение каждой подформулы. Таким образом, если n – это число переменных в формуле, а s – число выделенных подформул, то число столбцов в полной таблице истинности исходной формулы будет равно n+s, а число строк – 2n. При этом последний столбец этой таблицы будет представлять значения формулы.
Для примера рассмотрим
построение полной таблицы истинности
формулы
![]() .
Разделим её на подформулы: f1=x,
f2=f1y,
f3=f2z.
Тем самым, таблица будет содержать 8
строк и 6 столбцов. См. таблицу 3.
.
Разделим её на подформулы: f1=x,
f2=f1y,
f3=f2z.
Тем самым, таблица будет содержать 8
строк и 6 столбцов. См. таблицу 3.
|
x |
y |
z |
f1 |
f2 |
f3 |
|
0 |
0 |
0 |
1 |
1 |
0 |
|
0 |
0 |
1 |
1 |
1 |
1 |
|
0 |
1 |
0 |
1 |
1 |
0 |
|
0 |
1 |
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
0 |
1 |
|
1 |
0 |
1 |
0 |
0 |
1 |
|
1 |
1 |
0 |
0 |
1 |
0 |
|
1 |
1 |
1 |
0 |
1 |
1 |
|
Таблица 3 |
|||||
В последнем столбце таблицы 3 находятся значения исходной формулы.
Сокращенная таблица истинности строится непосредственно под формулой. Для этого выписывают саму формулу, затем под именами переменных записывают столбцы их значений, а под каждой логической связкой – столбец результатов соответствующей логической операции.
|
(( |
x |
|
y) |
|
z) |
|
|
1 |
0 |
1 |
0 |
0 |
0 |
|
|
1 |
0 |
1 |
0 |
1 |
1 |
|
|
1 |
0 |
1 |
1 |
0 |
0 |
|
|
1 |
0 |
1 |
1 |
1 |
1 |
|
|
0 |
1 |
0 |
0 |
1 |
0 |
|
|
0 |
1 |
0 |
0 |
1 |
1 |
|
|
0 |
1 |
1 |
1 |
0 |
0 |
|
|
0 |
1 |
1 |
1 |
1 |
1 |
Таблица 4 |
Рассмотрим построение
сокращенной таблицы истинности на
примере той же формулы:
![]() .
См. таблицу 4.
.
См. таблицу 4.
Внизу таблицы стрелками указаны участвующие в операции столбцы, номером в кружочке отмечен порядок выполняемых действий. Столбец результатов отмечен номером 3.
Из рассмотренных примеров видно, что значениями формулы могут быть только 0 или 1. Поэтому столбец результатов можно рассматривать, как некоторую истинностную функцию, принимающую те же значения, что и формула, на соответствующих «энках». Об этой функции говорят, что она реализуется формулой, про формулу, – что она реализует функцию.
Две формулы А и В называются эквивалентными, если функции fA и fB, соответствующие им, эквивалентны или равны, т.е. fA=fB. Для обозначения эквивалентных формул традиционно используется запись А=В, которую называют тождеством.
Следующие тождества характеризуют важнейшие свойства элементарных функций: {0, 1, , &, }. (Обозначим «∘» любую из функций: {&, , }.)
-
((x∘y)∘z)=(x∘(y∘z)) – свойство ассоциативности;
-
(x∘y)=(y∘х) – коммутативность;
-
конъюнкция и дизъюнкция дистрибутивны друг относительно друга: ((x y) & z) = ((x & z) (y & z)) ((x & y) z) = ((x z) & (y z));
-
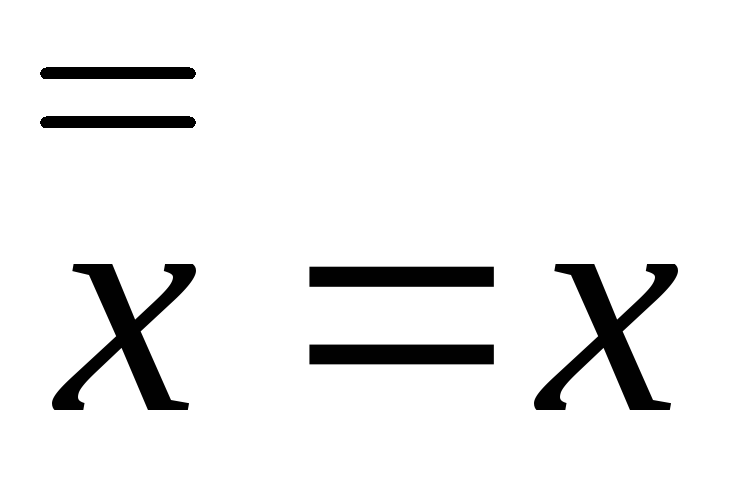 – закон двойного отрицания;
– закон двойного отрицания; -
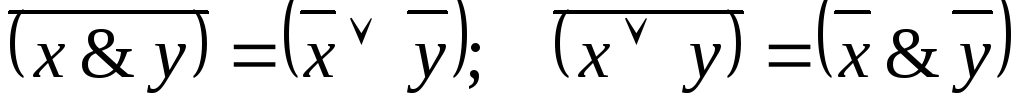 – законы Де Моргана для конъюнкции и
дизъюнкции;
– законы Де Моргана для конъюнкции и
дизъюнкции; -
(х & х) = x; (x x) = x – законы идемпотентности;
-
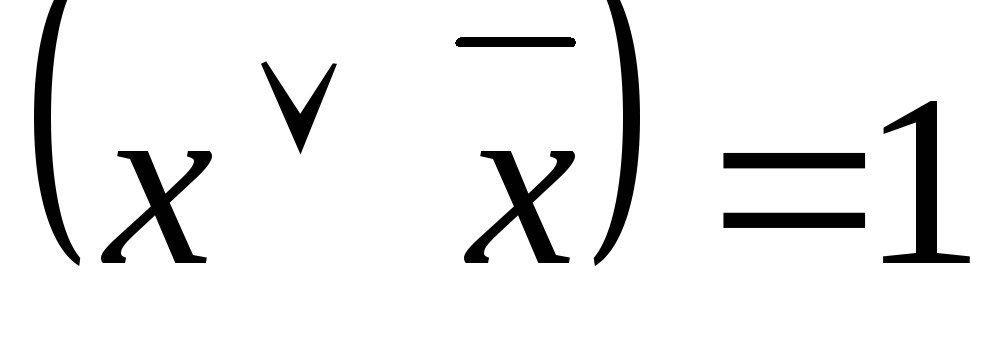 – закон исключенного третьего;
– закон исключенного третьего; -
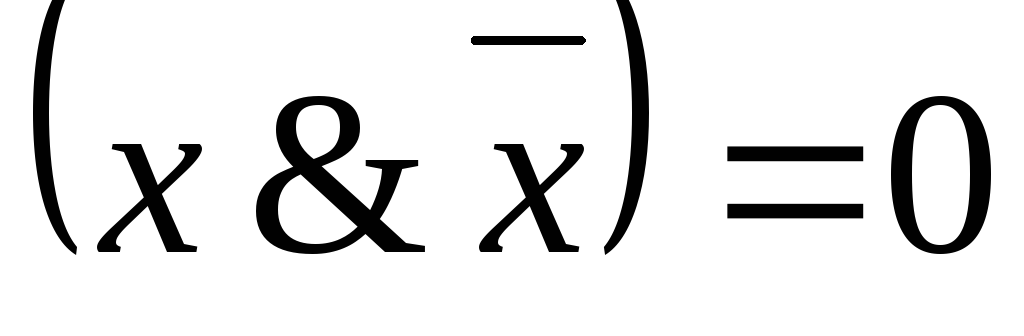 – закон противоречия;
– закон противоречия; -
(х & 0) = 0, (x 0) = x – умножение на ноль и сложение с нулем;
-
(х & 1) = х, (x 1) = 1 – умножение на единицу и сложение с единицей;
-
((х & y) x) = x, ((х y) & x) = x – законы поглощения.
Все тождества легко проверяются с помощью таблиц истинности.
Из свойств элементарных функций следует ряд простых правил преобразования формул:
а) если хотя бы один из сомножителей логического произведения равен нулю, то значение произведения также равно нулю;
б) если логическое произведение содержит не менее двух сомножителей, один из которых равен единице, то этот сомножитель можно сократить;
в) если логическая сумма содержит не менее двух слагаемых, одно из которых принимает значение ноль, то его можно сократить;
г) если хотя бы одно из слагаемых логической суммы принимает значение единица, то и вся логическая сумма равна единице;
д) пусть U1 – подформула формулы U; если в формуле U заменить любые вхождения подформулы U1 эквивалентной ей формулой В1, то в результате будет получена формула В, эквивалентная исходной формуле U.
Для упрощения записи формул вводятся следующие соглашения:
1) В формулах опускают
внешнюю пару скобок, т.е. вместо формулы
(ху) пишут
выражение ху.
Аналогично в выражениях со знаком
отрицания вместо
![]() записывают
записывают
![]() .
.
2) По закону ассоциативности для операции «∘» вместо формулы ((x ∘ y) ∘ z) или (x∘(y ∘ z)) используется выражение без скобок: x∘ y ∘ z. Для восстановления формулы достаточно расставить скобки, порядок которых не является существенным для вычислений.
3) О старшинстве операций: если в выражении с помощью скобок специально не указан порядок выполнения операций, то одинаковые по старшинству операции выполняются последовательно слева направо. Если в выражении имеются различные операции, то сначала выполняется отрицание, затем конъюнкция, дизъюнкция, импликация и т.д., самой последней выполняется эквиваленция. Скобки восстанавливаются по тому же правилу.
Ввиду введенного старшинства операций не всякая формула может быть записана без скобок. Например, в выражениях х(уz) или х&(yz) дальнейшее исключение скобок невозможно, т.к. это может повлиять на значение, вычисленное по формуле.
4) Для компактности
вместо записи х1&x2&…&xs
используется запись
![]() ,
а вместо х1x2…xs
–
,
а вместо х1x2…xs
–
![]() .
.
Перечисленные свойства и правила позволяют преобразовывать формулы, получая новые тождества.
Рассмотрим эквивалентные
преобразования формулы:
![]() 1=
1=
![]() 2=
2=
![]() 3=
3=
![]() 4=
4=
![]() 5=
5=
![]()
Тождество 1 записано по правилу сокращения единичного сомножителя, тождество 2 – по правилу замены подформулы эквивалентной формулой, а именно: здесь для замены использовался закон исключенного третьего. В тождестве 3 применен закон дистрибутивности. Тождество 4 получено по закону коммутативности. И, наконец, тождество 5 записано по закону поглощения, причем для наглядности «поглощающие элементы» подчеркнуты одинарной и двойной чертой.