Вариант №6

I.1. А = [–25; 1]– отрезок числовой оси

В = {–1; 0; 1} – трехэлементное множество

С = (0; +∞) – интервал на числовой оси

2. , где Γ - множество всех целых чисел за исключением нуля, т.е.

Γ = {1, –1, 2, –2, 3, –3,…} и

3.

4. (А \ В) (В \ А) = А В

II.1. Р₁ = {(а, 2); (а, 4); (а, 3); (с, 1); (с, 2); (с, 3)}

Р₂ = {(1, 1); (1, 4); (2, 3); (3, 3); (4, 1); (4, 3); (4, 4)}

2. P Í ℝ² и Р = {(x, y) : x + y = –2, где x, y Îℝ}

3. f(x) = (x – 1)² + 1; g(x) = x + 1; А = [0.5; 3]; В = [2; 3]

III.1.

2. x ≡ (y z) и (x ≡ y) (x ≡ z)

3.

IV.2.

3.

V.1. f (0,0,1) = f (0,1,1) = f (1,1,0) = 0

2.

Вариант №7

I.1. А = (–10; 5]– полуинтервал на числовой оси

В = [0; 10] – отрезок числовой оси

С = (4; +∞) – интервал на числовой оси

2. , где Γ - множество всех целых чисел за исключением нуля, т.е.

Γ = {1, –1, 2, –2, 3, –3,…} и

3.

4. ((АВ) \ С) = (А \ (В С)) (В \ (А С))

II.1. Р₁ = {(а, 1); (b, 2); (b, 3); (с, 1); (с, 3); (с, 4)}

Р₂ = {(1, 1); (1, 2); (1, 3); (2, 2); (2, 3); (3, 3); (3, 4); (4, 1); (4, 4)}

2. P Í ℝ² и (x, y) , x, y Îℝ.

3. f(x) = (x – 1)²; g(x) = x; А = [0.5; 3]; В = [1; 2]

III.1.

2. x ↓(y z) и (x ↓y) (x ↓ z)

7.

IV.2.

3.

V.1. f (1,0,0) = f (0,0,1) = f (0,1,1) = 0

2.

Вариант №8

I.1. А = (–∞; 2]– полуинтервал на числовой оси

В = [–3; 3] – отрезок числовой оси

С = (0; 4) – интервал на числовой оси

2. , где ℕ - множество всех натуральных чисел и

3.

4.

II.1. Р₁ = {(а, 3); (b, 4); (b, 3); (с, 1); (с, 2); (с, 4)}

Р₂ = {(1, 2); (1, 3); (1, 4); (2, 3); (4, 3); (4, 2)}

2. P Í ℝ² , (x, y) и x, y Îℝ.

3. f(x) = – (x + 1)² –1; g(x) = x–1; А = [–1.5; 1]; В = [–3; –2]

III.1.

2. x (y z) и (x y) (x z)

3

IV.2.

3.

V.1. f (0,0,1) = f (0,1,1) = f (1,0,0) = f (1,0,1)=1

2.

Вариант №9

I.1. А = (–2; 3) – интервал на числовой оси

В = [0; 4] – отрезок числовой оси

С = {2; 3} – двухэлементное множество

2. , где ℕ – множество всех натуральных чисел и

3.

Если

4.

II.1. Р₁ = {(а, 3); (b, 4); (b, 3); (b, 1); (b, 2); (c, 2)}

Р₂ = {(1, 1); (1, 3); (2, 4); (3, 1); (3, 3); (4, 2)}

2. P Í ℝ² , (x, y) , где x, y Îℝ.

3. f(x) = 1– (x + 1)²; g(x) = x+1; А = [–1.5; 1]; В = [–1; 0]

III.1.

2. x → (y ≡ z) и (x →y) ≡ (x → z)

3.

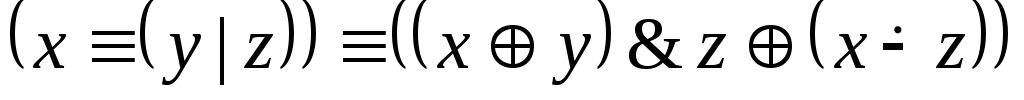
IV.2.

3.

V.1. f (1,0,0) = f (0,1,1) = f (0,1,0) = 0

2.