1.В чем состоит основной принцип выделения границ области устойчивости в пространстве параметров?

При конструировании следящих систем обычно возникает задача: при каких значениях параметров система сохраняет устойчивость?

Поставим задачу более конкретно: пусть в характеристическом уравнении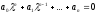 (9.1) не заданы некоторые коэффициенты. Предлагается в пространстве этих коэффициентов выделить множество, все точки которого гарантируют отрицательность действительных частей корней уравнения (9.1).

Без потери общности достаточно рассмотреть случай двух не заданных коэффициентов (рис.9.1).

Рис.9.1. Область устойчивости в пространстве двух коэффициентов.

При пересечении границы выделенной области один или несколько корней характеристического уравнения переходят из левой полуплоскости в правую. Это рассуждение дает способ построения границы области устойчивости: в характеристическом уравнении нужно заменить на 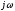, после чего уравнение вида (9.1) станет параметрически заданным уравнением границы устойчивости. Рассмотрим несколько примеров, демонстрирующих описанный прием построения границы.

2.Изложить аналитический подход к исследованию многомерной системы управления. Распространение понятия свертки на многомерные системы.

Задачу интегрирования уравнений с переменными параметрами можно считать в большинстве случаев принципиально решенной, если иметь в виду численные методы. Поэтому главное внимание мы уделим здесь проблеме качественной оценки асимптотического поведения нестационарных систем на уровне универсальных теоретических выводов.

Введем понятие функциональной матрицы

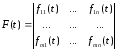. (17.1)

Если существуют производные всех элементов матрицы (17.1), то производной матрицы F (t) будем называть матрицу, аналогичную (17.1), в которой все элементы заменены соответствующими производными.

Далее, пусть уравнение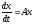 (17.2) имеет совокупность решений 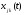. В таком случае говорят, что они образуют фундаментальную систему если:

1.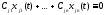 тогда и только тогда, есл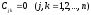и и

2. Любое решение уравнения (17.2) может быть записано в виде суммы

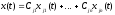. (17.3)

Говорят также, что совокупность решений 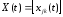образует фундаментальную матрицу решений. В векторной форме любое решение уравнения (17.2) можно записать как 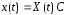, (17.4) где 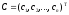- столбец из постоянных коэффициентов.

Форма (17.4) используется для метода вариации постоянных Лагранжа при решении неоднородных систем вида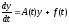. (17.5)

Решение записывается как произведение, (17.6)где X (t) – фундаментальная матрица решений однородного уравнения (17.2) и u (t) – некоторая вектор-функция.

Подставив (17.6) в (17.5), имеем 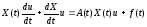, или, имея в виду (17.2), .

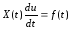Отсюда непосредственно следует .

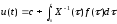Следовательно, решение неоднородного уравнения (17.5) запишется в виде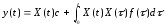. (17.7)

Для определения постоянного вектора с положим t = t₀. Тогда .

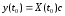Отсюда, умножая слева на матрицу X^-1( t₀ ), получаем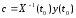.(17.8)

Наконец, подставив (17.8) в (17.7), находим окончательно искомое решение неоднородного уравнения (17.5), удовлетворяющее начальным условиям 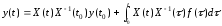.(17.9)

На формулу (17.9) можно взглянуть с еще одной точки зрения. Очевидно, что если матрица X (t) – фундаментальная матрица решений однородной системы (17.2), то и произведение также фундаментальная матрица этой системы. Очевидно, что при постоянной матрице A 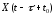также удовлетворяет уравнению (17.2).

Пусть система (17.2) удовлетворяет условиям единственности решения и 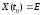. Тогда при .

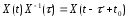В силу предположения о выполнении условий единственности решения последнее равенство справедливо и при остальных значениях переменной t. В частности, если t₀=0 и y(0)=0, формулу (17.9) можно записать в знакомом виде . (17.12)

Следует обратить внимание на то, что мы нигде не использовали понятия функции Дирака, а последнее равенство записано в векторной форме.

БИЛЕТ № 19