1.Выделение области устойчивости в пространстве двух параметров. Особые прямые. Правила штриховки границы.

Обратимся к случаю двух незаданных параметров, которые входят линейно в характеристическое уравнение. В частном случае такими параметрами могут быть два коэффициента уравнения (9.1) . В общем случае при замене 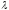на 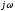характеристическое уравнение распадается на два, которые образуют систему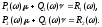 (9.3)с двумя незаданными параметрами 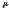и . Система имеет единственное решение, если ее определитель не равен нулю. В случае линейной зависимости уравнений они выражают одно и то же уравнение прямой, которая называется особой.

При вычислении определителя системы следует помнить, что его знак меняется при перестановке строк и столбцов. Знак же определителя системы, отображающей плоскость корней на плоскость параметров устанавливает правило обхода замкнутого контура. Рис.9.4 поясняет сказанное.

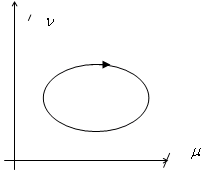
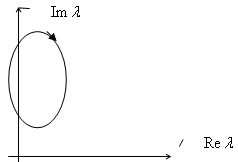
Рис.9.4. Направление обхода контура сохраняется при положительном определителе системы. Справа остается внутренняя область контура.

В соответствии с уравнениями (9.3) система координат должна быть правой.

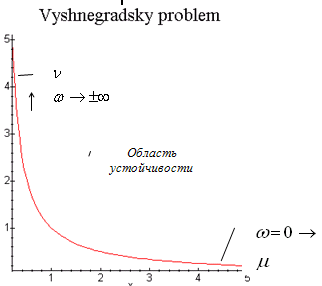
В качестве примера рассмотрим классическую задачу Вышнеградского.

Пример 3.

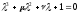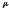Характеристическое уравнение имеет вид ,и требуется выделить область устойчивости на плоскости параметров и . Заменив 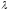на 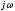,получаем систему из двух уравнений 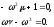(9.4). Решение ее очевидно – ,граница устойчивости представляет собой гиперболу Для выяснения того, с какой стороны гиперболы находится область устойчивости необходимо вычислить определитель системы (9.4) Таким образом, при движении вдоль гиперболы область устойчивости должна оставаться слева, ибо при 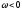определитель положителен. После изменения знака определителя область устойчивости остается справа (рис.9.5). Гипербола проходится дважды и, следовательно, при ее пересечении два корня характеристического уравнения пересекают мнимую ось. Этот факт, впрочем, можно установить элементарным путем, если положить 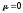и Тогда получается уравнение 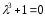с одним отрицательным корнем, равным –1, и двумя корнями с положительной действительной частью 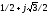и

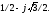
2.Сформулировать условия устойчивости линейной системы управления с медленно меняющимися параметрами.

Для дальнейшего исследования устойчивости нам понадобится лемма Гронуолла-Беллмана.

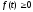Пусть и при 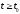,, причем при справедливо неравенство , где c - положительная постоянная. Тогда .

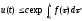Пользуясь леммой, рассмотрим устойчивость линейной дифференциальной системы с почти постоянной матрицей.

Теорема. Пусть система 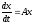, (17.10) где A – постоянная матрица, устойчива в смысле Ляпунова. Тогда система 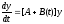,(17.11) где 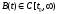и также устойчива.

Доказательство.

Пусть X (t) - фундаментальная матрица решений системы (17.10) и X(0)=E . Рассматривая B (t) y как возмущение в (17.11) и пользуясь выводом (17.12) метода вариации постоянных, запишем .

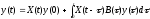Т.к. система (17.10) устойчива, то ее фундаментальная матрица решений ограничена, т.е. .

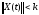Следует оценка сверху .

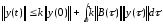Теперь используем лемму Гронуолла-Беллмана, согласно которой

.

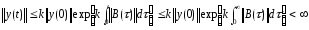Таким образом, система (17.11) также устойчива, что и требовалось.

В качестве простого примера рассмотрим уравнение вида 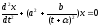. (17.12)

Вводя обозначение 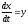, приведем его к нормальной форме Коши. Очевидно, что в данном случае постоянная матрица .

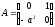Сравнение с (17.11) позволяет записать также .

Принимая в качестве нормы наибольшую абсолютную величину элементов, имеем .

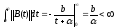Согласно теореме, предшествующей примеру, решение должно оставаться ограниченным.