1.Практическое применение критерия устойчивости Гурвица (не ниже 4-го порядка).

Алгебраический критерий Гурвица.

Для того, чтобы корни алгебраического уравнения имели отрицательные вещественные части необходимо и достаточно, чтобы определитель вида и все его диагональные миноры имели знак, одинаковый с a₀ .

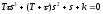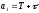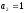. (7.3),где , , и .

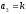2.Модификация критерия Гурвица для дискретных систем.

Выяснить вопрос о наличии или отсутствии условия устойчивости помогает критерий, представляющий собой развитие критерия Гурвица. Итак, рассмотрим систему рекуррентных соотношений вида

. (14.8)

Характеристическое уравнение ее в матричной форме имеет вид

. (14.9)

Этот определитель можно записать и в обычной форме алгебраического уравнения степени k, т.е.

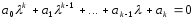.(14.10)

Решение системы (14.8) имеет вид

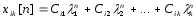, (i=1,2,…k).

Из решения непосредственно следует, что устойчивость его гарантируется при условии |лямбда| < 1. Для того, чтобы воспользоваться известным критерием Гурвица, преобразуем левую полуплоскость корней характеристического уравнения во внутренность окружности единичного радиуса. Это можно сделать при помощи дробно-линейного преобразования вида

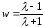(14.11)

Действительно, положив 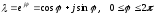, без труда обнаруживаем

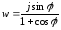, т.е.

точки окружности переходят в точки мнимой оси и обратно, причем точка лямбда=0 внутренности окружности переходит в точку w= -1 левой полуплоскости.

Подставив (14.11) в (14.10), после приведения к общему знаменателю и группировки слагаемых с одинаковыми степенями получаем полином степени k, к которому следует применить критерий Гурвица. Если при этом обнаруживается, что Re w < 0, то следствием будет неравенство | λ | < 1.

БИЛЕТ № 15

1.Доказать критерий устойчивости а.В. Михайлова.

Критерий Михайлова был разработан в 30-х г.г. ХХ столетия. Для его вывода рассмотрим характеристический полином, т.е. выражение вида , (8.1)

в котором положим , и проследим за изменением аргумента вектора 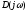при . Очевидно, изменение аргумента отдельных сомножителей в (8.1) будет зависеть от того, в какой части плоскости расположен корень (рис.8.1). Это изменение будет равно 180^о , если корень расположен в левой полуплоскости и –180^о в противоположном случае. Таким образом, приращение аргумента вектора 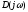равно

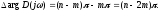
Рис.8.1. Расположение корней характеристического полинома

Здесь m – число корней с положительной действительной частью. Если все корни характеристического полинома имеют отри-цательную вещественную часть, то изменение аргумента характеристического полинома составит

Этот критерий обычно формулируется несколько иначе. Если принять во внимание, что годограф характеристического полинома симметричен относительно вещественной оси, то достаточно проследить за изменением его аргумента лишь при положительных значениях частоты. При m=0 оно составит . Иными словами:

для того, чтобы характеристический полином (8.1) имел все корни с отрицательной вещественной частью необходимо, чтобы его годограф монотонно проходил n квадрантов комплексной плоскости.

2.Управляемость динамических систем. Теорема Калмана об управляемости.

запишем соответствующее дифференциальное уравнение в наиболее общем виде .

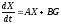Здесь X=( x₁,x₂,…x_n ) ^T – вектор состояния, G=( g₁,g₂,…g_m) ^T – вектор управления,A - квадратная матрица порядка n. В соответствии с введенными обозначениями матрица , не обязательно квадратная и некоторые ее элементы могут быть нулями

Некоторые компоненты вектора X или их линейные комбинации можно измерить. Совокупность измеренных координат мы будем обозначать вектором Y = ( y₁,y₂,…y_q ) ^T , а его связь с компонентами вектора состояния выражается соотношением Y = CX, где C – некоторая, вообще говоря, прямоугольная матрица .

Определение

Система называется управляемой, если существует ограниченный вектор управления G , под действием которого она переводится за конечное время из любого начального состояния X в начало координат X=(0,0,…0)^T.

Если это свойство относится не ко всем компонентам вектора состояния, то система не полностью управляема. В частности, система может оказаться и полностью неуправляемой (если ни по какой координате система не обладает свойством управляемости).

Теорема Калмана.

Составим матрицу из n строк и nm столбцов .

Система будет полностью управляемой, если ранг матрицы K равен n.

Пример 15.1. Пусть система описывается уравнениями

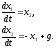
Запишем матрицы , 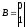и .

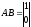Составим матрицу Калмана .

Определитель этой матрицы не равен нулю, следовательно ее ранг равен 2 и система управляема.

БИЛЕТ № 16