16. Динамика вращательного движения

 Описанное нами движение твердого тела относительно неподвижной точки является основным видом движения. Однако вычислить вектор – момент импульса системы относительно произвольной точки – не просто: надо знать шесть проекций (три задают положение тела, три задают положение точки).         Значительно проще найти момент импульса  тела, вращающегося вокруг неподвижной оси  z  (рис. 6.4). В этом случае составляющие  – момента внешних сил, направленные вдоль x и y, компенсируются моментами сил реакции закрепления. Вращение вокруг оси z происходит только под действием  M_z .

  Гироскоп.

       Пусть некоторое тело вращается вокруг оси z (рис. 6.5).

Рис. 6.4	Рис. 6.5

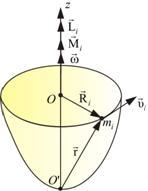
       Получим уравнение динамики для некоторой точки  m_i  этого тела, находящегося на расстоянии  R_i  от оси вращения. При этом помним, что и  направлены всегда вдоль оси вращения z, поэтому

     или      .

       Поскольку  у всех точек разная, введем вектор угловой скорости , причем  . Тогда  .         Так как тело абсолютно твердое, то в процессе вращения  m_i  и  R_i  останутся неизменными. Тогда

       Обозначим  I_i  – момент инерции точки находящейся на расстоянии R от оси вращения:

.

(6.2.1)

       Момент инерции тела служит мерой инертности во вращательном движении.         В общем случае тело состоит из огромного количества точек, и все они находятся на разных расстояниях от оси вращения. Момент инерции такого тела равен:

.

(6.2.2)

       Как видно, момент инерции I – величина скалярная.         Просуммировав (6.2.1) по всем i-м точкам, получим    или

.

(6.2.3)

       Это основное уравнение динамики тела, вращающегося вокруг неподвижной оси. (Сравним:  – основное уравнение динамики поступательного движения тела).         Для момента импульса  тела, вращающегося вокруг оси z, имеем:

,    ,    .

(6.2.4)

(Сравним:  – для поступательного движения).         При этом помним, что  и  - динамические характеристики вращательного движения, направленные всегда вдоль оси вращения. Причем  определяется направлением вращения, как и , а направление  зависит от того, ускоряется или замедляется вращение.

15. Вращение вокруг неподвижной оси

Вращением вокруг неподвижной оси называется такое движение твердого тела, при котором во все время движения две его точки остаются неподвижными. Прямая, проходящая через эти точки, называется осью вращения. Все остальные точки тела движутся в плоскостях, перпендикулярных оси вращения, по окружностям, центры которых лежат на оси вращения. Положение вращающегося твердого тела определяется одним параметром - углом φ между начальным положением АМ₀О некоторой плоскости, связанной с телом и проходящей через ось, и ее положением АМО в данный момент времени (рис. 1).

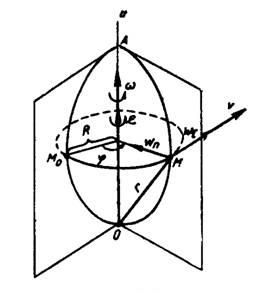
Рисунок 1.

Закон вращательного движения:

Проекция вектора угловой скорости на ось и определяется зависимостью:

Угловая скорость ω рад/сек связана с числом оборотов в минуту n зависимостями:

Проекция вектора угловой скорости на ось u определяется зависимостью

Скорость и ускорение точки М вращающегося твердого тела определяются соотношениями (рис. 1):

или в скалярной форме:

Частные случаи:

1) равномерное вращение (ε=0):

2) равнопеременное вращение (ε_u=const):

14. Простра́нство Минко́вского ― четырёхмерное псевдоевклидово пространство сигнатуры , предложенное в качестве геометрической интерпретации пространства-времени специальной теории относительности.

Каждому событию соответствует точка пространства Минковского, в лоренцевых (или галилеевых) координатах, три координаты которой представляют собой декартовы координаты трёхмерного евклидова пространства, а четвёртая ― координату ct, где c ― скорость света, t ― время события. Связь между пространственными расстояниями и промежутками времени, разделяющими события, характеризуется квадратом интервала:

(Нередко в качестве квадрата интервала берется противоположная величина, выбор знака — вопрос произвольного соглашения. Так, первоначально сам Минковский предложил именно противоположный знак для квадрата интервала).

Интервал в пространстве Минковского играет роль, аналогичную роли расстояния в геометрии евклидовых пространств. Он инвариантен при замене одной инерциальной системы отсчета на другую, так же, как расстояние инвариантно при поворотах, отражениях и сдвигах начала координат в евклидовом пространстве. Роль, аналогичную роли вращений координат в случае евклидова пространства, играют для пространства Минковского преобразования Лоренца.

Интервал аналогичен квадрату расстояния в евклидовом пространстве. В отличие от последнего интервал не положителен, также между различными событиями интервал может быть равен нулю.

13. Преобразова́ния Ло́ренца — линейные (или аффинные) преобразования векторного (соответственно, аффинного) псевдоевклидова пространства, сохраняющее длины или, что эквивалентно, скалярное произведение векторов.

Преобразования Лоренца псевдоевклидова пространства сигнатуры (n-1,1) находят широкое применение в физике, в частности, в специальной теории относительности (СТО), где в качестве аффинного псевдоевклидова пространства выступает четырёхмерный пространственно-временной континуум (пространство Минковского).
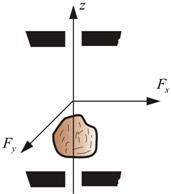
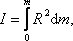