2. Классическое, статистическое и геометрическое определения вероятности.

Классическое определение вероятности было введено Лапласом и относится к равновозможным (равновероятным) событиям.

Понятие равновозможных событий не определяется, а лишь поясняется примерами. Для каждого из таких событий характерно то, что ни одно из них не является объективно более возможным, чем другие. В практической задаче исследователь сам решает, какие события считать равновозможными.

Пример 2.1. При бросании игральной кости события e₁, e₂, e₃, e₄, e₅, e₆ (см. пример 1.1) считаются равновозможными. Но событие A=e₂, e₄, e₆– «появление четного числа очков при бросании игральной кости», очевидно, должно происходить на практике чаще, чем, например, событие e₅, значит, считать А и e₅ равновозможными нельзя.

События «выпадение решки» и «выпадение орла» при одном подбрасывании монеты считаются равновозможными.

Определение 1 (классическое определение вероятности).

Пусть n число всех элементарных исходов опыта, которые образуют полную группу попарно несовместных и равновозможных событий, а m – число тех из них, которые благоприятны событию А.

Тогда вероятностью события А называется число

Р(А)=. (2.1)

Так, в примере 2.1 число всех исходов n=6, e₅ наступает лишь в одном из шести случаев, поэтому Р(e₅)=1/6. Событию А благоприятны три элементарных исхода, следовательно, Р(А)=3/6=1/2.

Из определения вероятности следует, что для любого события А 01, причем Р(V)=0, а Р(U)=1.

Пример 2.2. Пусть опыт состоит в последовательном бросании двух игральных костей. Найдем вероятность события В – «при бросании костей в сумме выпало 8 очков» и вероятность события С– «при бросании в сумме выпало 12 очков».

Очевидно, что при бросании двух игральных костей всего может быть получено 36 равновозможных элементарных исходов: n=36 (каждому из шести различных случаев выпадения очков на первой кости отвечает шесть случаев выпадения различного числа очков на второй кости).

Событию С благоприятен лишь один исход: случай выпадения двух шестерок, поэтому m(С)=1, и Р(С)=1/36.

Событию В благоприятны 5 исходов (2+6, 3+5, 4+4, 5+3, 6+2), и, следуя Лапласу, получаем Р(В)=5/36.

Пример 2.3. Пусть в коробке имеется 2 красных, 2 белых и 6 синих шаров. Наудачу вынимаем два шара. Какова вероятность событий А – «вынуты два красных шара» и В – «вынуты два синих шара»?

Число всех исходов испытания равно числу способов вытащить 2 шара из 10: , причем все исходы равновозможны.

Исход, благоприятный событию А, только один (поскольку красных шаров всего 2), следовательно, Р(А)=1/45.

Число исходов, благоприятных событию В, равно числу способов вытащить 2 шара из 6: , значит, Р(В)=15/45=1/3.

Замечание. Классическое определение вероятности не требует того, чтобы испытания практически проводились, достаточно лишь посчитать теоретически число всех исходов и число благоприятных, а затем применить формулу (2.1). Но она может быть использована лишь в случае, когда все события равновозможны и образуют полную группу попарно несовместных событий.

Вернемся к обсуждению понятия равновозможности.

Пример 2.4. Допустим, что два стрелка стреляют по мишени. Если события «попадание» и «промах» равновозможны, то вероятность попадания каждого равна 1/2. Но если первый стрелок является профессионалом, а второй, например, никогда не брал в руки винтовку, то вероятность их попадания, очевидно, разная. Как оценить их возможности? Обычно эта оценка дается из практики. Если первый стрелок попадает 98 раз из 100 выстрелов, а второй – только 10, то за вероятность попадания первого стрелка логично принять Р₁=98/100=0,98 , а за вероятность попадания второго – Р₂=10/100=0,1.

Р₁ и Р₂ в данном примере – статистические значения вероятности.

Определение 2 (статистическое определение вероятности).

Предположим, что некоторое испытание, в результате которого может наступить событие А, проведено N раз, и при этом событие А появилось ровно M раз. Тогда число

(2.2)

называется статистической вероятностью (или относительной частотой) события А в рассматриваемой серии испытаний.

Пример 2.5. Рождается ребенок – мальчик или девочка. Кажется, что эти события равновозможны, т.е. вероятность рождения мальчика равна 1/2. Но статистика рождений не вполне согласуется с нашим «кажется». В разное время в различных странах мальчиков рождается несколько больше, чем девочек – примерно 518 мальчиков на каждую тысячу детей. Значит, статистическая вероятность рождения мальчика равна .

Замечание. Подчеркнем еще раз, что в отличие от классического определения вероятности, статистическая вероятность может быть вычислена в том случае, если испытания действительно проводились.

Практика показывает, что в тех случаях, когда точно известна вероятность Р(А) в классическом понимании, при достаточно большом числе N проведенных испытаний . Это приближенное равенство получило теоретическое обоснование в законе больших чисел, открытом Я. Бернулли. Этот закон мы рассмотрим ниже.

Часто при решении задач мы сталкиваемся с событиями, вычислить вероятность которых мы не можем с помощью классического или статистического определения. Такая ситуация возникает в случае, когда число различных исходов испытания бесконечно.

Если множество Е всех исходов опыта есть, например, некоторое множество на плоскости, то можно воспользоваться следующим геометрическим определением вероятности.

Определение 3 (геометрическое определение вероятности).

Пусть на плоскости задана некоторая область D, площадь которой равна S(D), и в ней содержится область d, площадь которой равна s(d). В области D наудачу ставится точка. Предположим, что вероятность попадания точки в какую-либо часть D пропорциональна площади этой части и не зависит от ее расположения и формы. Тогда вероятность события А – «точка попадает в область d» равна числу

. (2.3)

Замечание. Если множество Е всех исходов опыта есть подмножество одномерного или трехмерного пространства, то геометрическая вероятность вычисляется аналогично, только в определении фигурирует не площадь множества, а длина или объем.

Пример 2.6. Найдем вероятность того, что сумма длин двух отрезков, длина каждого из которых меньше или равна 2, будет больше 2.

Пусть событие А – «сумма длин отрезков больше 2». Обозначим через x и y длины первого и второго отрезков. По условию , . На плоскости множество, удовлетворяющее этим условиям, изображается квадратом со стороной 2.

Неравенство означает, что сумма длин отрезков больше двух. Множество точек d, удовлетворяющее данному неравенству, лежит выше прямой (см. рисунок 2.1). Площадь этого множества, очевидно, составляет половину площади квадрата. Событие А произойдет, если точка с координатами , наугад выбранная в квадрате D, попадет в область d, заданную неравенством .

Согласно геометрическому определению, вероятность А равна отношению площадей d и D, т.е. равна 1/2.

d

d

Рис. 2.1. Рис.2.2.

С помощью геометрического определения вероятности решается целый ряд задач, в формулировке которых совсем нет геометрических объектов. Покажем это на примере.

Пример 2.7 (задача о встрече). Два товарища условились встретиться в промежутке времени с 12 до 13 часов. Договорились, что тот, кто пришел первым, ждет другого в течение 20 минут, после чего уходит.

Найдем вероятность того, что встреча состоится. Пусть событие А – «товарищи встретились». Обозначим через x момент прихода одного из товарищей, через y – момент прихода второго. По условию x и y расположены в промежутке от 12 до 13 часов, можно считать, что и . Товарищи встретятся, если время прихода одного из них отличается от времени прихода второго не более, чем на 20 минут (1/3 часа), т.е. .

Задача переформулируется следующим образом: в квадрат D=(x,y): ,  наудачу ставится точка. Требуется найти вероятность того, что она попадет в область d = (x,y):  = (x,y): . Области D и d изображены на рис. 2.2. Площадь квадрата D равна 1, площадь области d легко вычисляется: s(d)=1-=. Следовательно, вероятность того, что товарищи встретятся, равна 5/9.

Невозможность строгого определения понятия равновероятных событий приводит к ряду противоречий между классическим и статистическим определениями вероятностей (см. примеры 2.4, 2.5). Во второй половине XIX и в начале XX века это послужило причиной сомнений в правильности и строгости построенной теории вероятностей, и некоторые известные математики перестали интересоваться этой теорией как математической дисциплиной. Этому способствовало и опубликование ряда парадоксов. Приведем здесь один из наиболее характерных – парадокс Бертрана.

Пример 2.8 (парадокс Бертрана).

Начертим окружность. Произвольным образом проведем хорду. Вычислим вероятность того, что хорда окажется длиннее стороны вписанного в окружность правильного треугольника.

Парадокс Бертрана состоит в том, что при разных способах решения этой задачи получаются разные ответы.

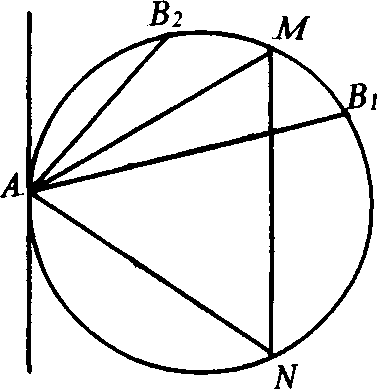
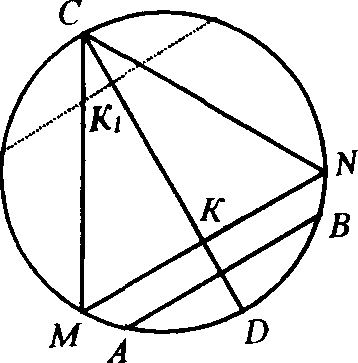
Рис. 2.3. Рис.2.4.

Первый способ решения. Обозначим хорду через АВ. Построим диаметр CD перпендикулярно этой хорде, а также параллельно хорде АВ сторону правильного вписанного треугольника MN (см. рис. 2.3). Обозначим через К точку пересечения MN и CD, а через К₁ – точку, симметричную К относительно центра окружности. Те хорды, которые пройдут параллельно АВ через точки отрезка КК₁, длиннее стороны MN, а те из них, которые пересекут диаметр CD вне отрезка КК₁, короче MN. С помощью формул элементарной геометрии легко подсчитать, что . Следовательно, вероятность того, что случайная хорда длиннее стороны MN, равна 1/2. Это первый ответ.

Второй способ решения. Допустим, что один конец произвольной хорды АВ закреплен в некоторой точке окружности. Пусть это точка А. Начертим правильный треугольник AMN, вписанный в окружность (рис. 2.4). Те хорды АВ, которые пересекают сторону MN треугольника (на рисунке это хорда АВ₁), длиннее стороны MN, а те хорды, которые лежат вне треугольника (на рисунке – хорда АВ₂), короче стороны. Можно предположить, что все хорды, проходящие через точку А, одинаково «плотно» распределены по углу QAP=180. Поскольку угол MAN правильного треугольника равен 60, то вероятность того, что случайная хорда превышает по длине сторону вписанного треугольника, равна 60/180=1/3. Второй ответ не совпадает с первым.

Третий способ решения. Можно рассуждать и следующим образом. Чтобы установить положение хорды, достаточно знать положение ее середины.

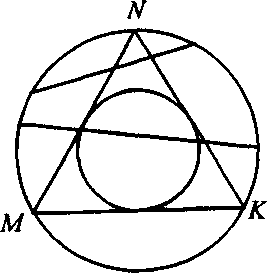
Рис. 2.5.

Ясно, что хорды, середины которых расположены внутри круга, вписанного в данный треугольник MNK, превышают сторону треугольника по длине (см. рис. 2.5). А хорды, середины которых лежат вне вписанного круга, оказываются меньше стороны MN. Таким образом, множество хорд, длина которых больше , может быть представлено площадью меньшего круга, а множество всех хорд данной окружности – площадью большего круга. Легко показать, что площадь меньшего круга составляет 1/4 площади большего. Следовательно, при данном способе рассуждений вероятность того, что случайная хорда длиннее стороны правильного вписанного в окружность треугольника, равна 1/4.

Три разных способа решения задачи дают три различных ответа. Разные результаты получаются потому, что мы по-разному определяли понятие «произвольной» хорды и рассматривали разные множества хорд. В первом случае мы двигали хорду по диаметру, принимали длину отрезка за меру множества точек на нем и вычисляли отношение длин отрезков. Во втором случае за меру множества точек принимали величину соответствующего угла и вычисляли отношение величин углов. В третьем случае за меру точек мы избрали площадь множества, в котором эти точки расположены, и вычисляли отношение площадей. Во всех трех способах рассуждения мы по-разному определяли понятие равновозможности. Поэтому и постановки задачи и ответы – разные.