3. Свойства . Бином Ньютона. Треугольник Паскаля.

Числа обладают многими интересными и важными свойствами. Сначала приведем два из них.

Первое свойство. .

Докажем это свойство, используя формулу (3.1).

.

Пользуясь первым свойством, можно упрощать вычисления, когда m>n/2. Например, если требуется вычислить , можно вычислить .

Втрое свойство.

Для доказательства свойства опять применим формулу (3.1).

.

Согласно второму свойству может быть вычислено через коэффициенты и , т.е. вычисляется через и ; числа и вычисляются через , и ; и т.д. Поэтому коэффициенты можно расположить в треугольной таблице, где каждый элемент в строке (кроме крайних) равен сумме двух элементов предыдущей строки, стоящих над ним:

(8.4)

и т.д.

Крайние элементы в любой строке равны единице: (не выбирать ни одного элемента из n или выбрать n элементов можно лишь одним способом). Кроме того, в силу первого свойства, коэффициенты в каждой строке, одинаково удаленные от и равны, т.е. таблица симметрична.

С помощью этой таблицы коэффициенты легко вычисляются:

1

1 1

1 2 1

1 3 3 1

1 4 6 4 1

и т.д.

Этот треугольник часто называют треугольником Паскаля. Однако, еще до Паскаля его знал итальянский математик Тарталья. А за много лет до Тартальи этот треугольник встречается в работах арабских математиков Гиясэддина и Омара Хайяма. Поэтому его также называют просто арифметическим треугольником.

Изучим далее свойства . Заметим, что хорошо известные формулы

,

можно записать и так:

,

(коэффициенты при a и b в правых частях формул совпадают с коэффициентами в соответствующих строках треугольника).

Аналогичные формулы справедливы для четвертой, пятой и вообще любой натуральной степени двучлена a+b.

Теорема. Для произвольных чисел a и b и произвольного натурального числа n справедлива формула

. (8.3)

Формула (8.3) носит имя великого английского физика и математика И. Ньютона (1643-1727). Это неверно с точки зрения истории математики. Формулу хорошо знали среднеазиатские математики Омар Хайям, Гиясэддин, в Западной Европе ее задолго до Ньютона знал Б.Паскаль. Заслуга Ньютона была в том, что он обобщил эту формулу на случай нецелых n. Тем не менее, сейчас разложение (8.3) называют обычно биномом Ньютона. Коэффициенты называются биномиальными коэффициентами.

Используя знак суммы, формулу Ньютона можно записать короче:

.

Доказательство формулы (8.3) проводится методом математической индукции. Мы не приводим его здесь.

Пример 8.1. Возведем в шестую степень двучлен .

Положив в формуле (8.3) , , n=6, имеем

.

Пример 8.2. Найдем четвертый член разложения степени бинома 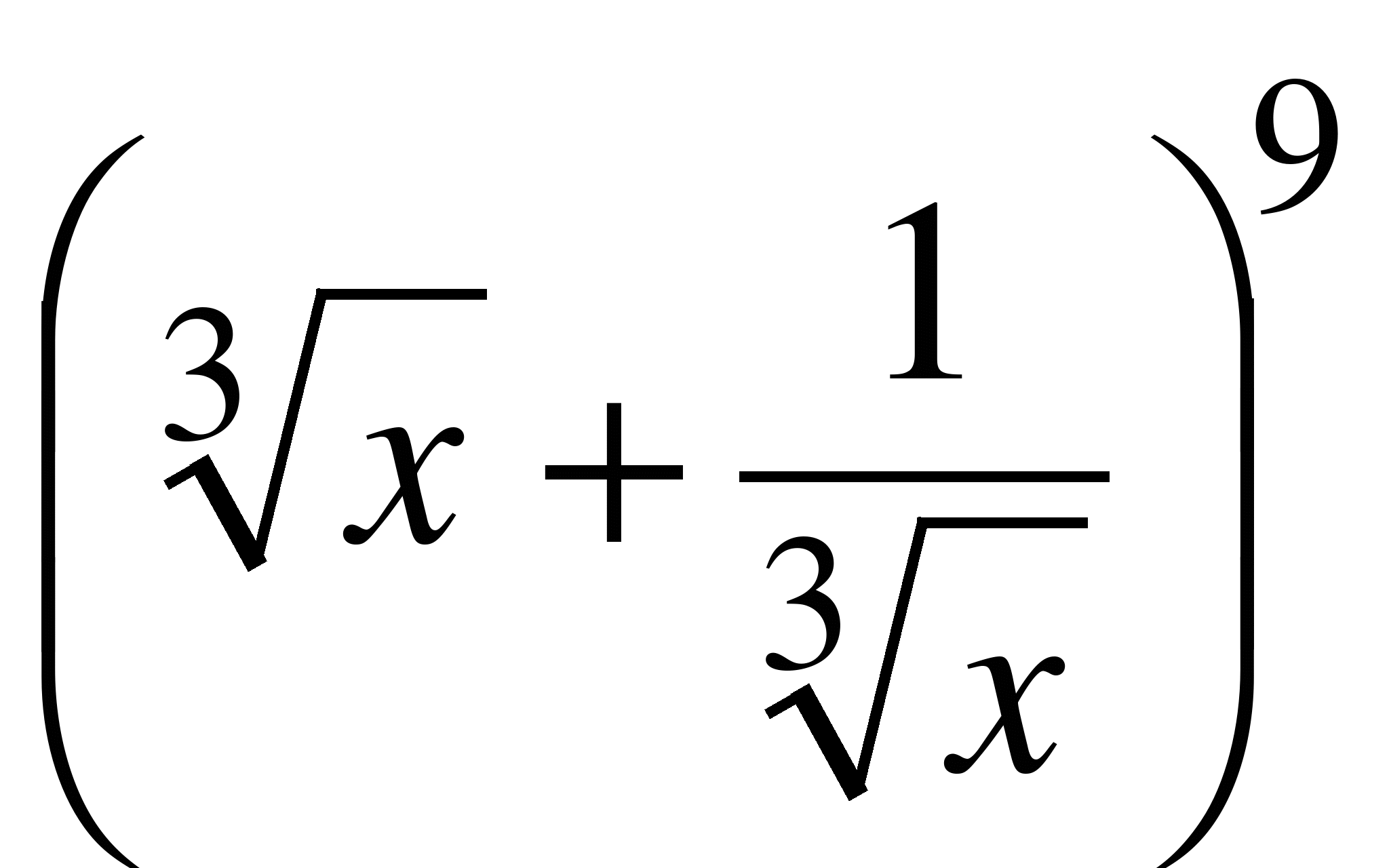. Согласно формуле (8.3) он равен .

Приведем еще два свойства биномиальных коэффициентов.

Третье свойство. .

Это свойство легко доказать с помощью формулы (8.3). Положив в формуле a=1, b=1, будем иметь .

Четвертое свойство. .

Для доказательства этого свойства достаточно положить в формуле (8.3) a=1 и b= -1.