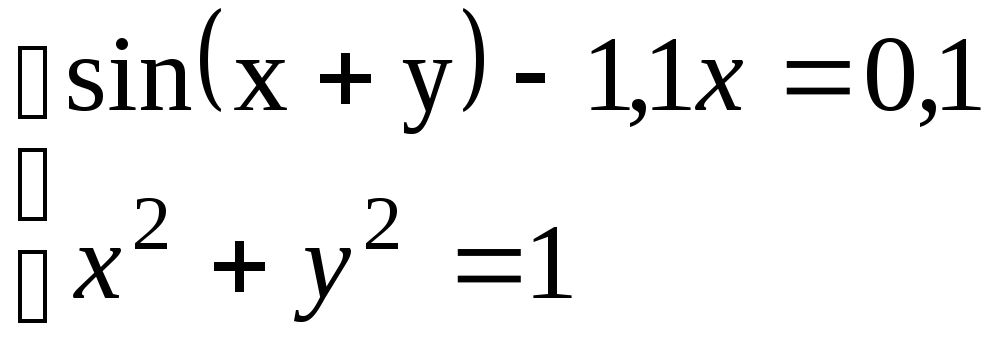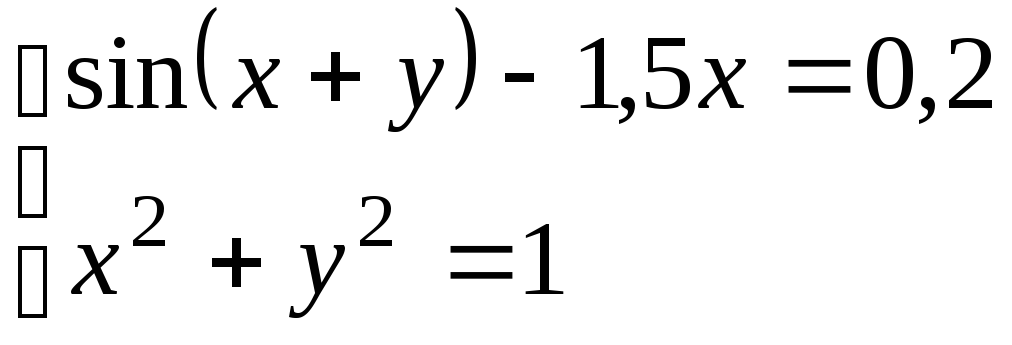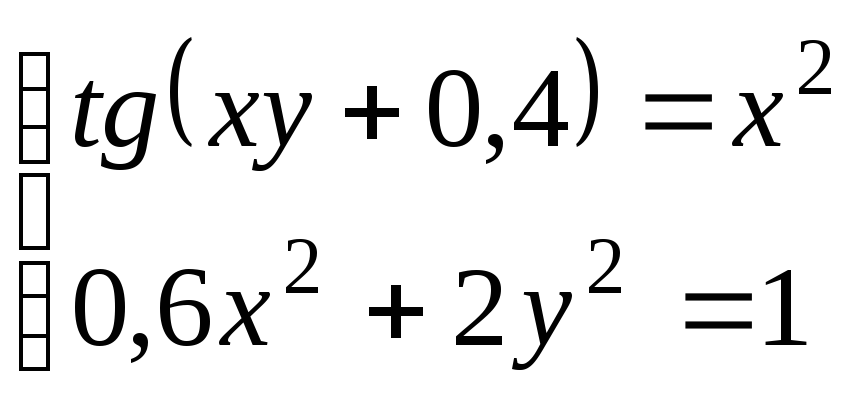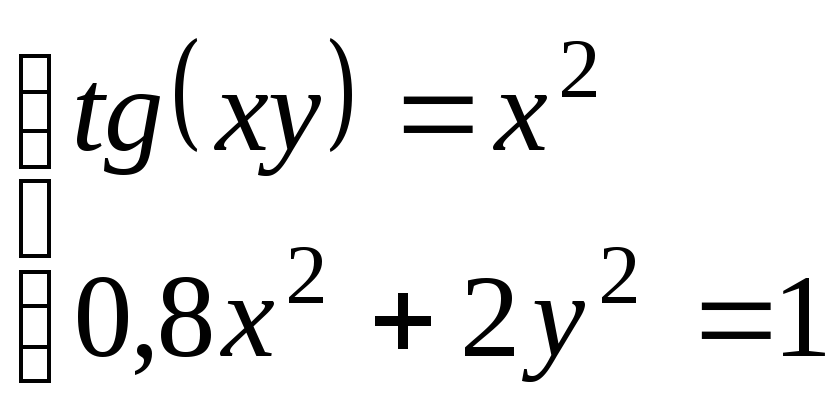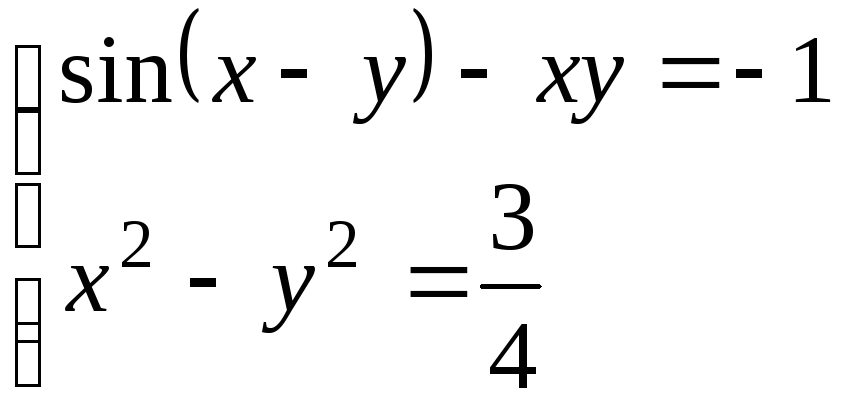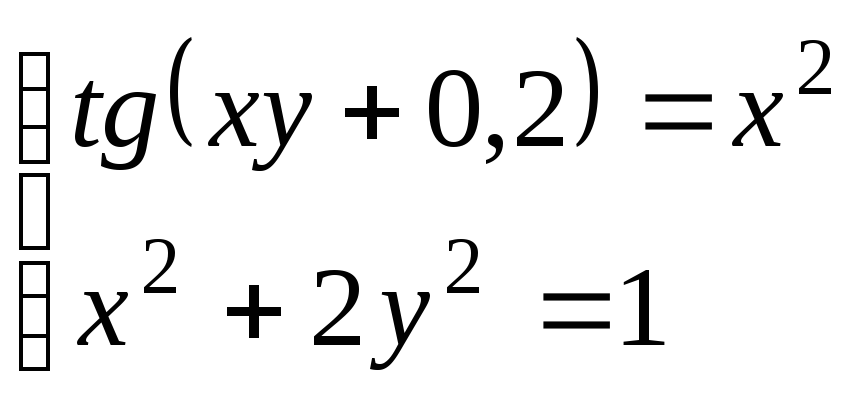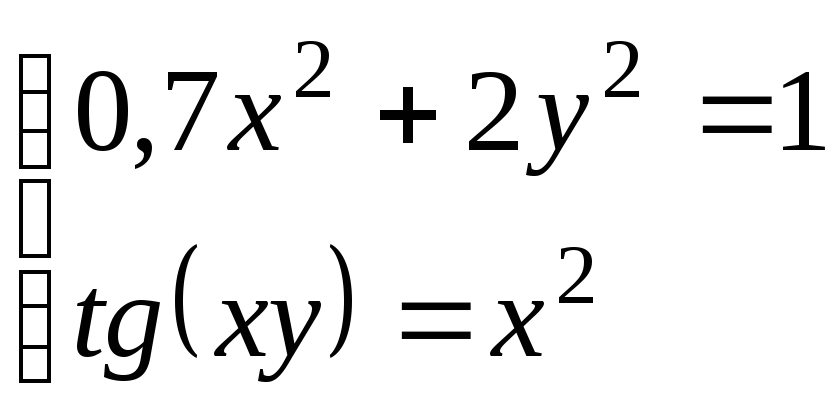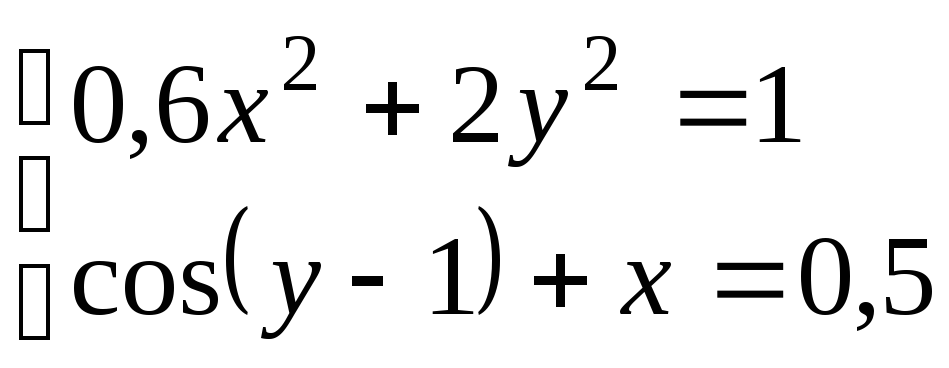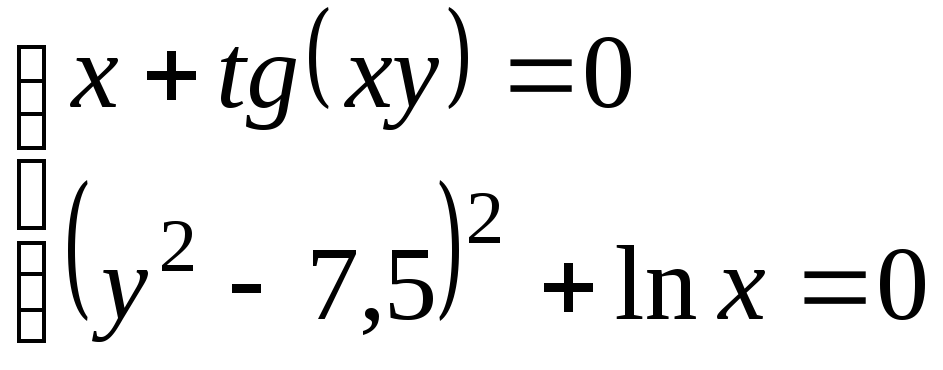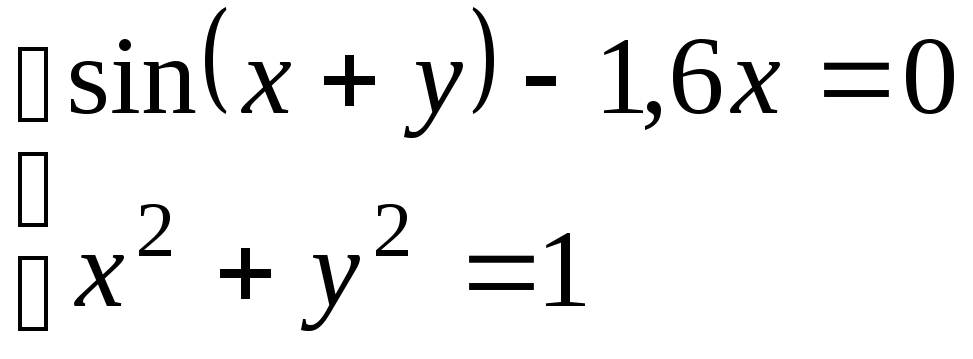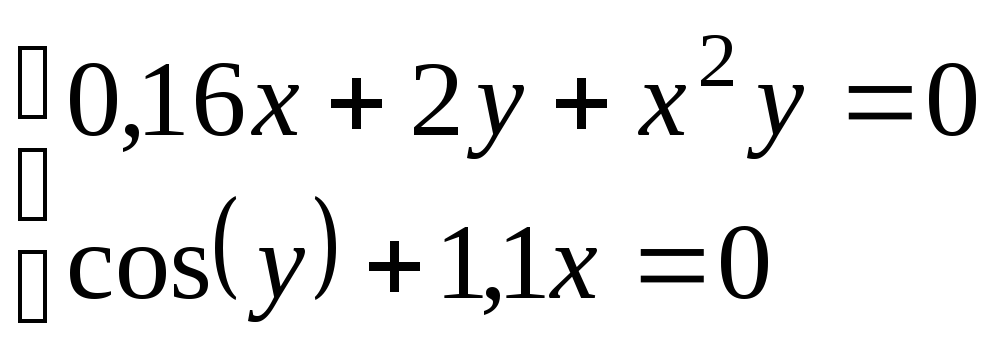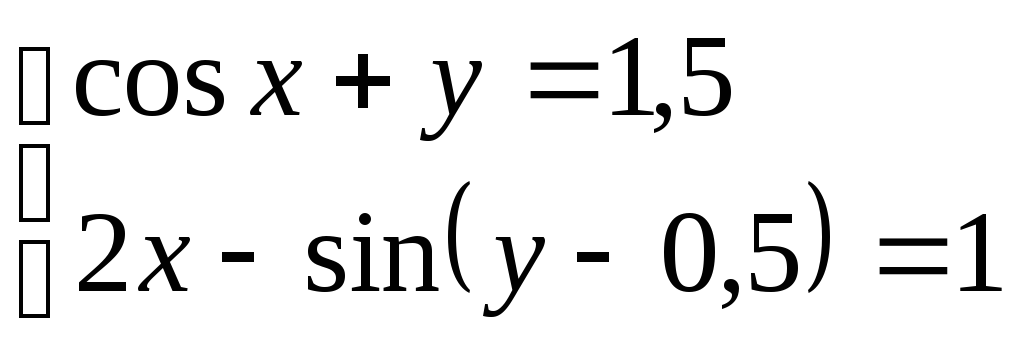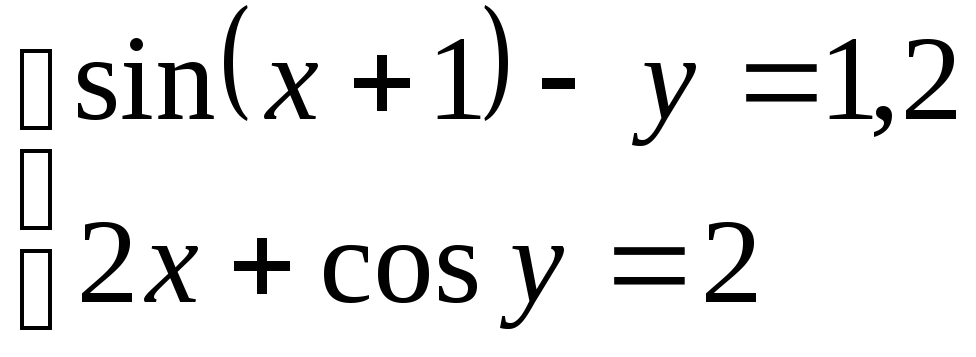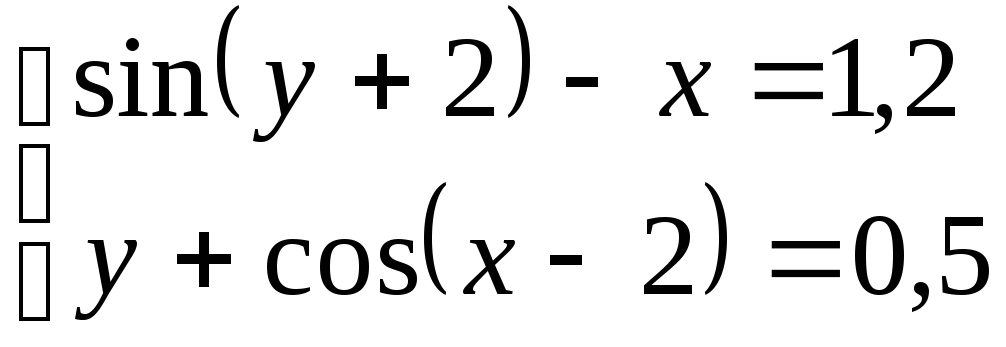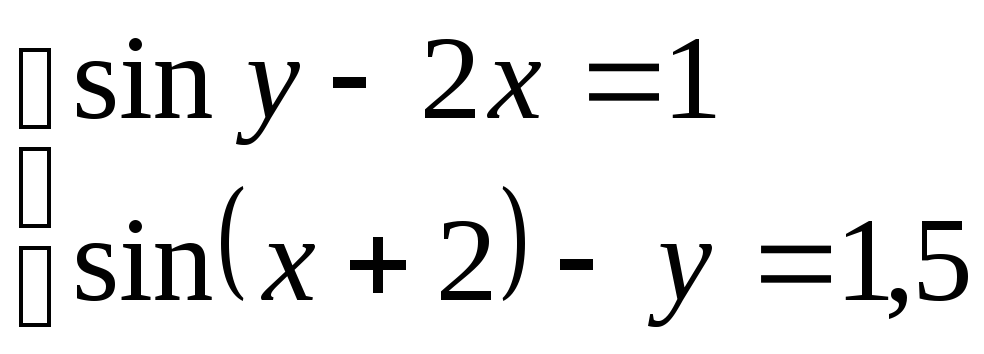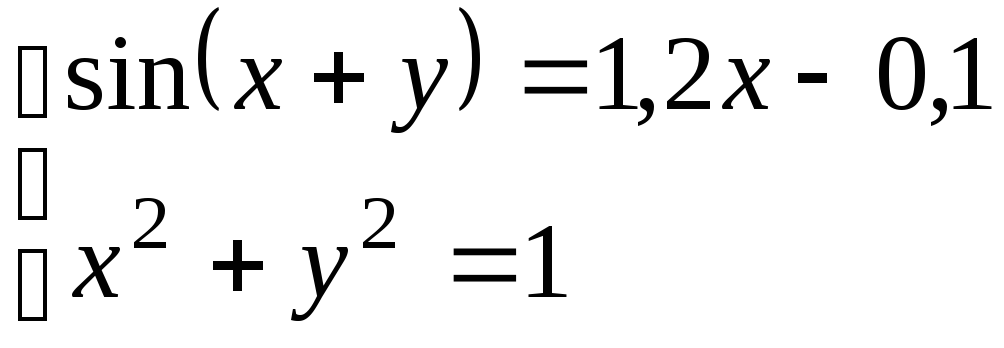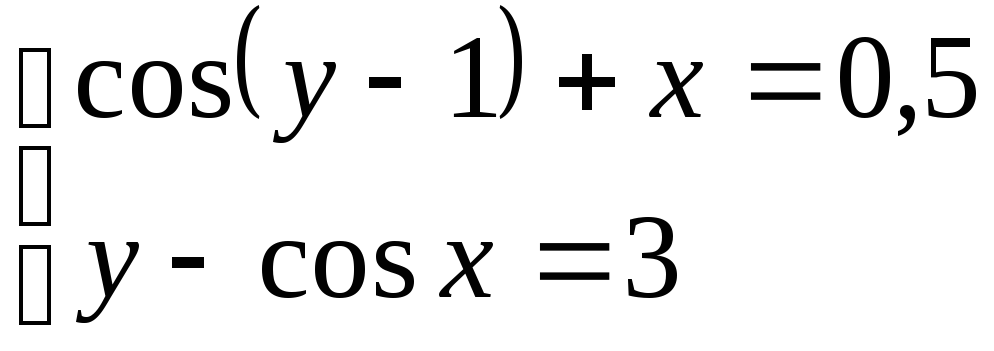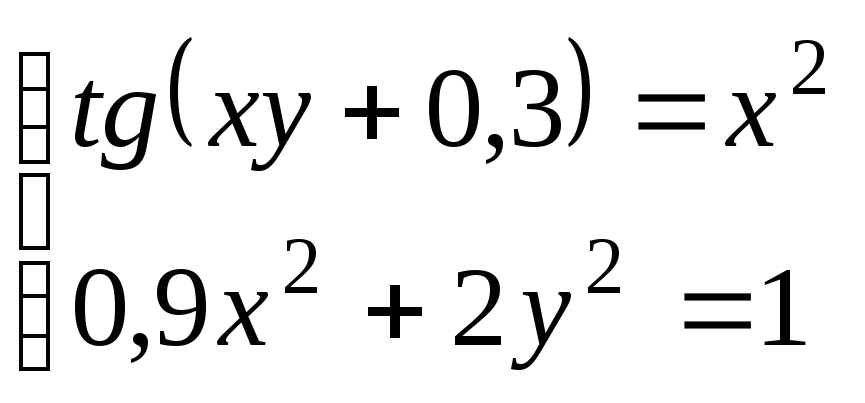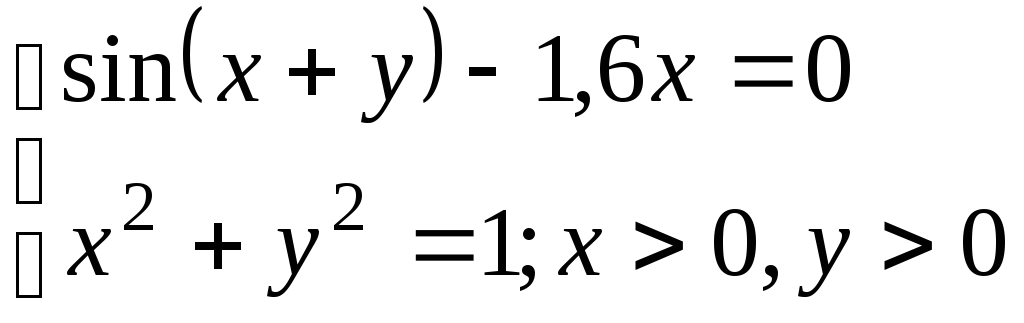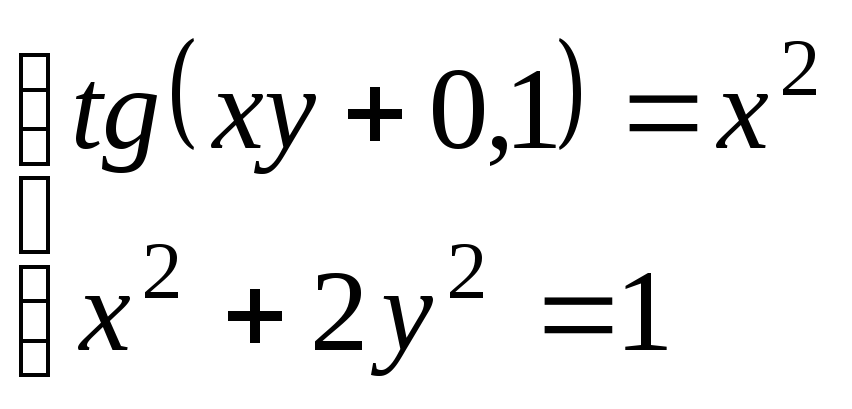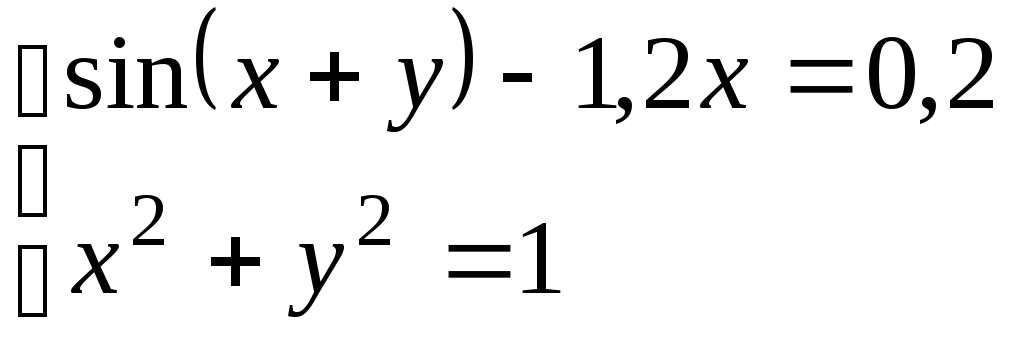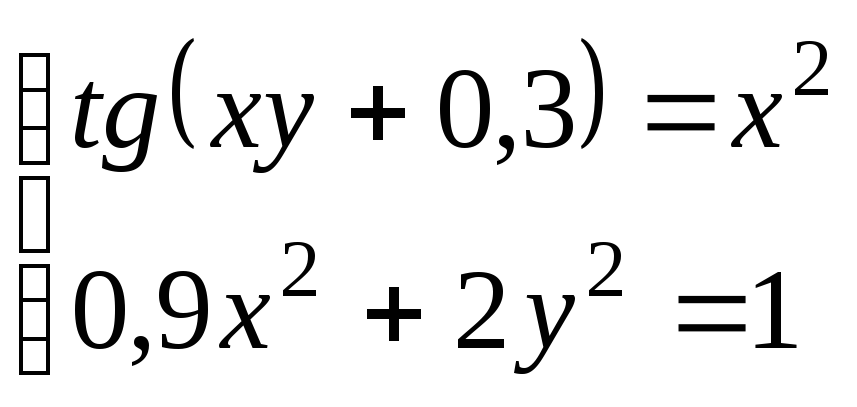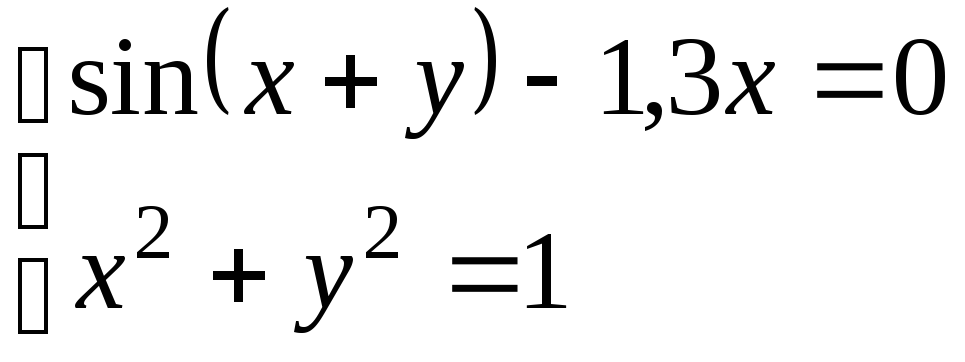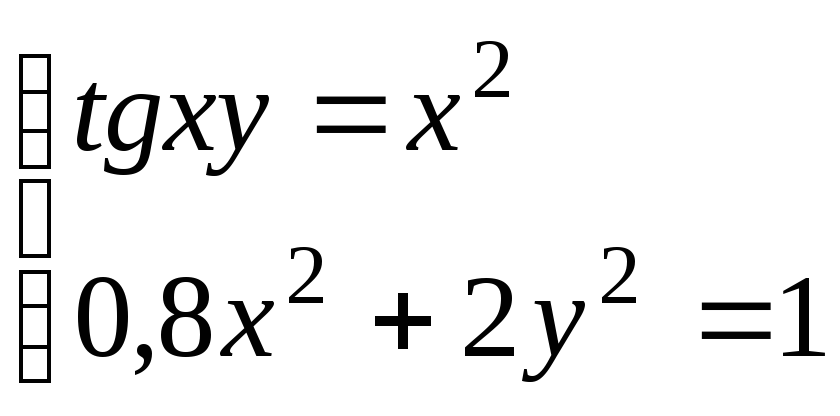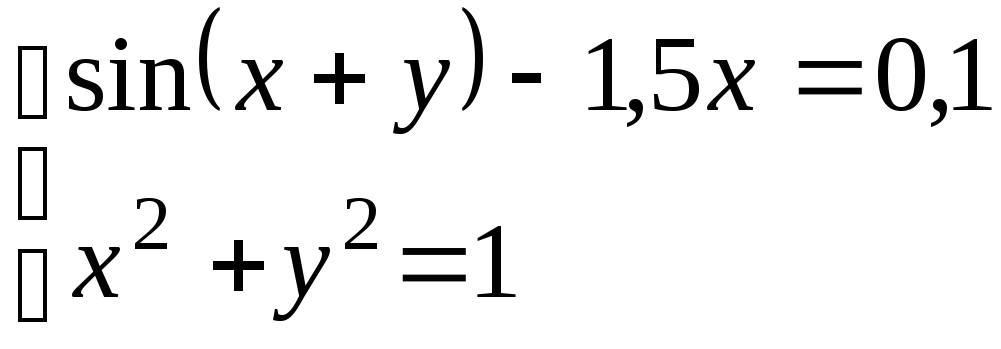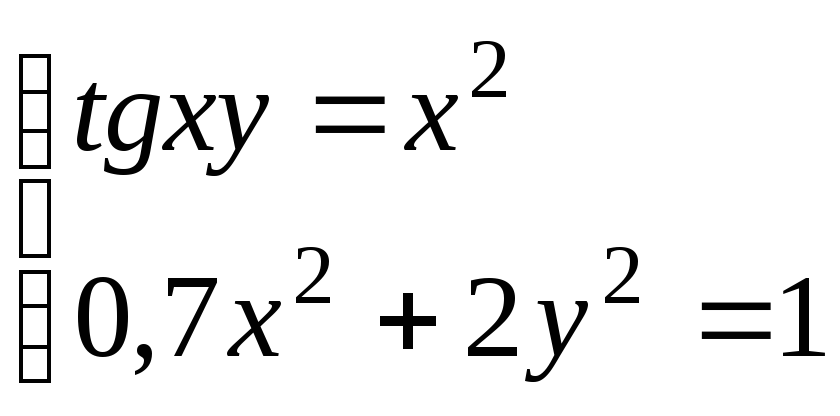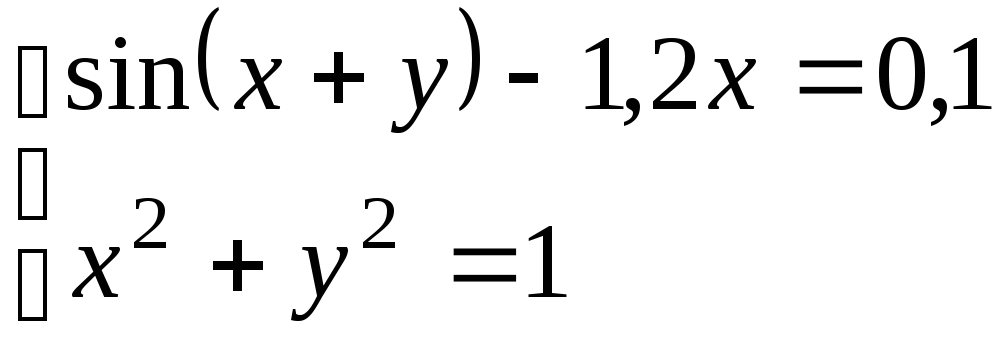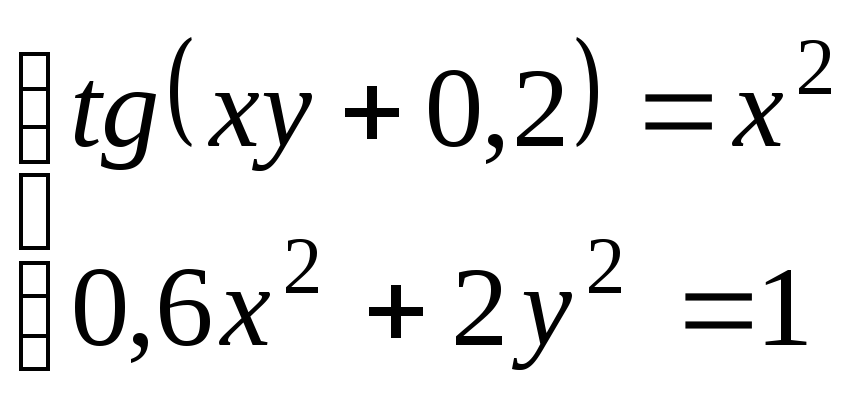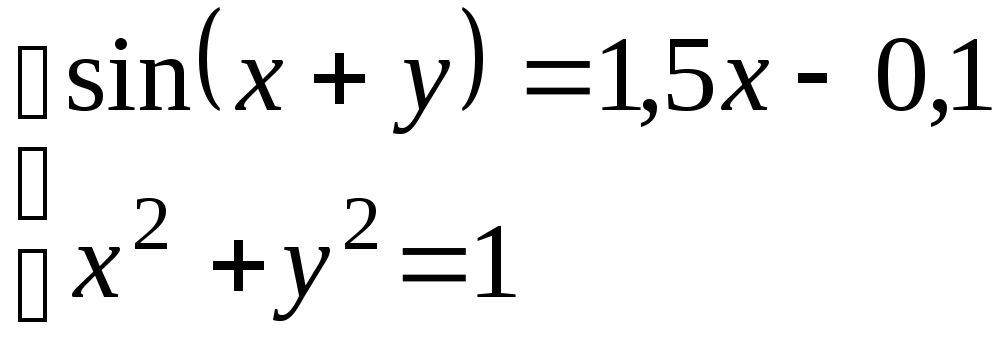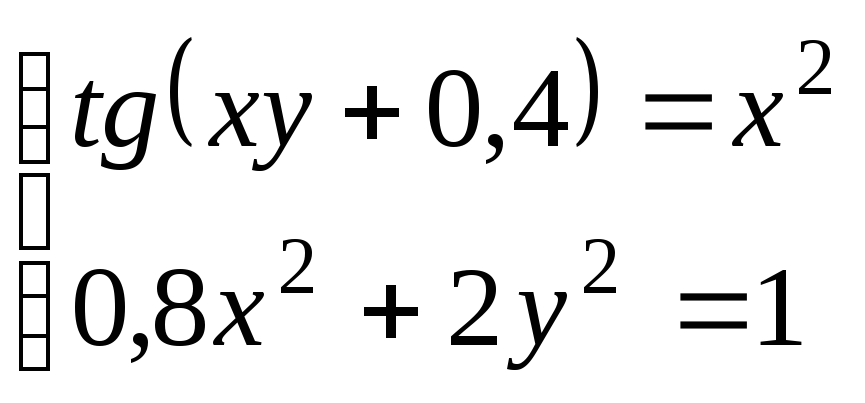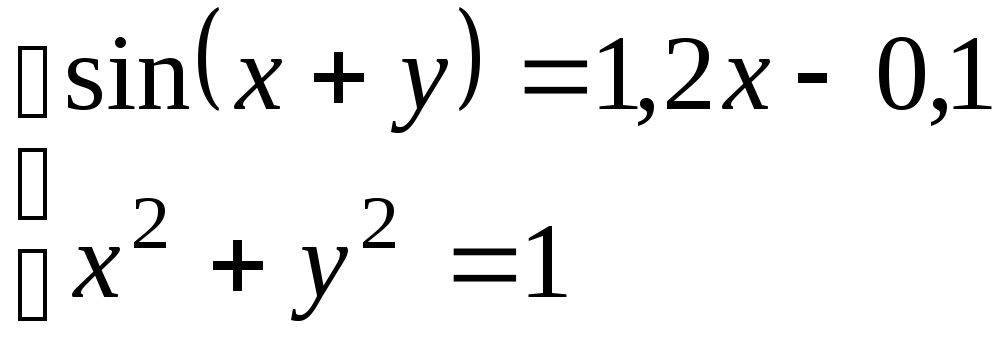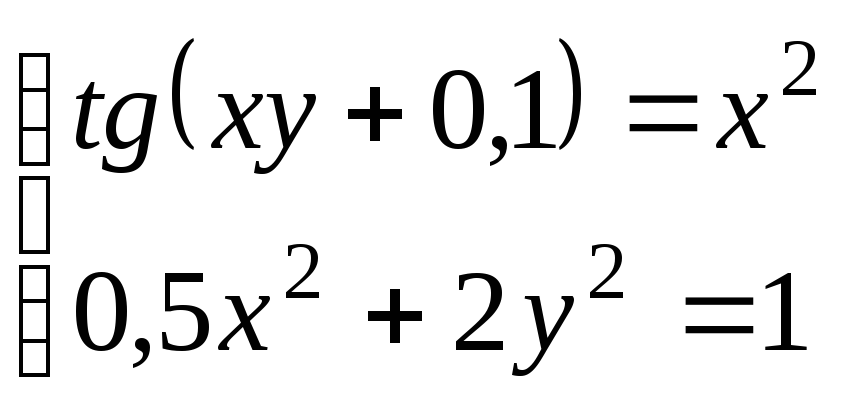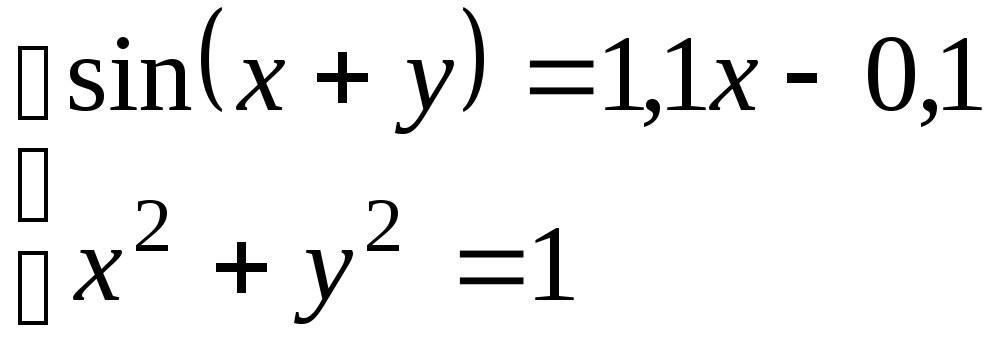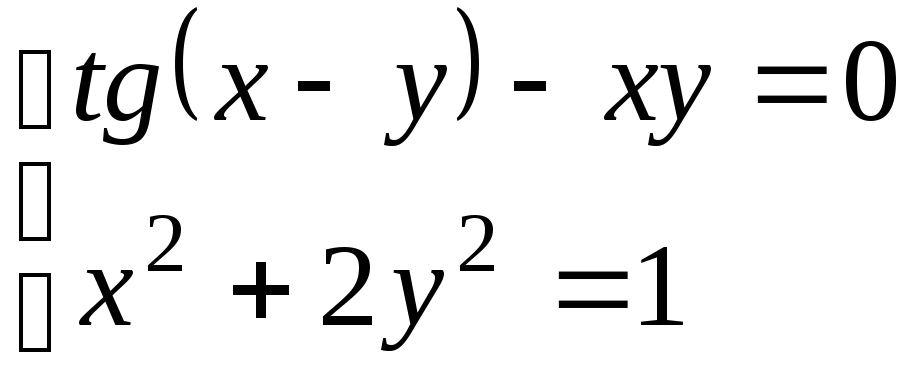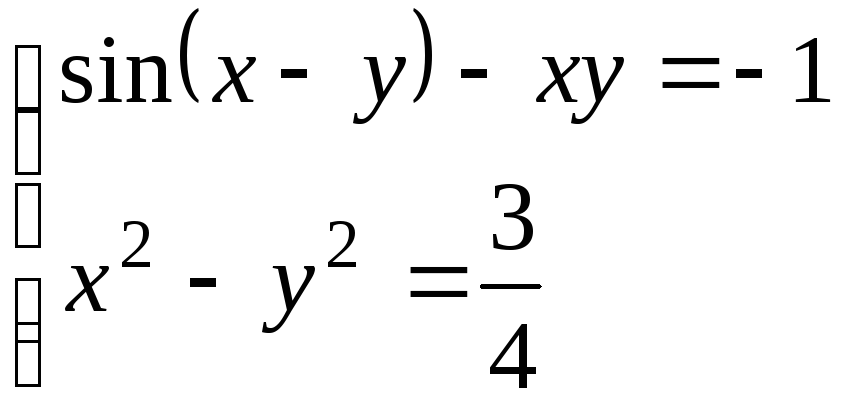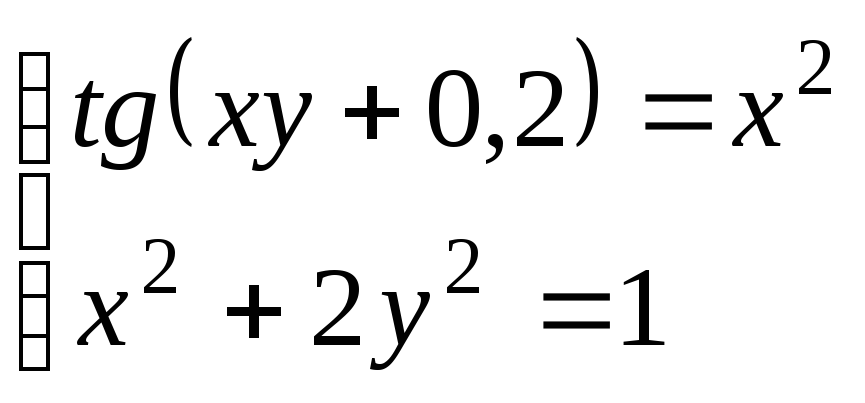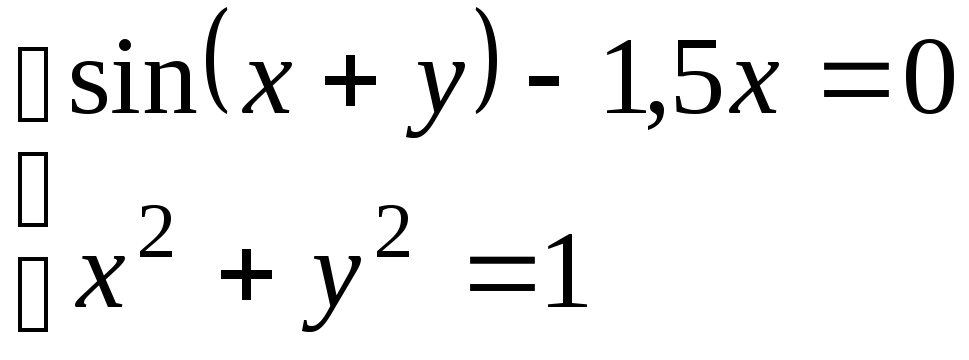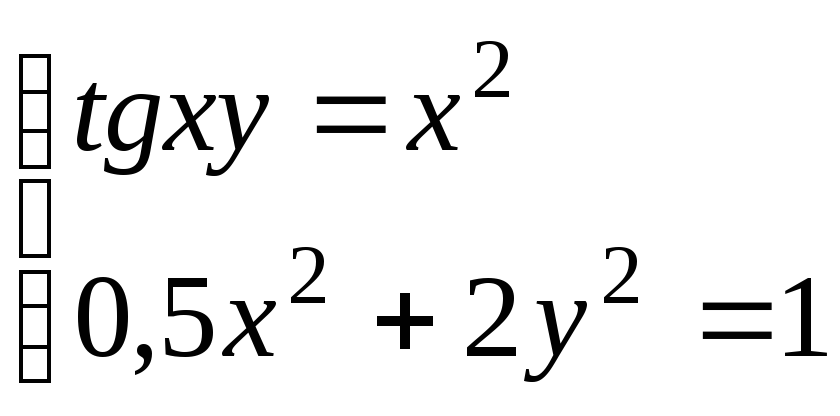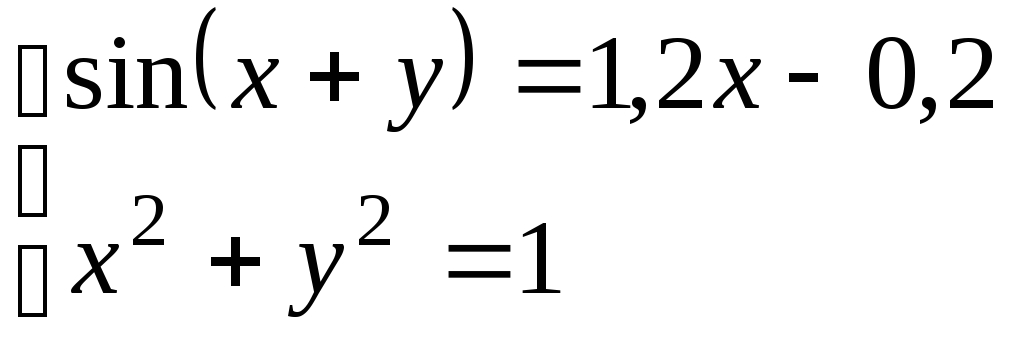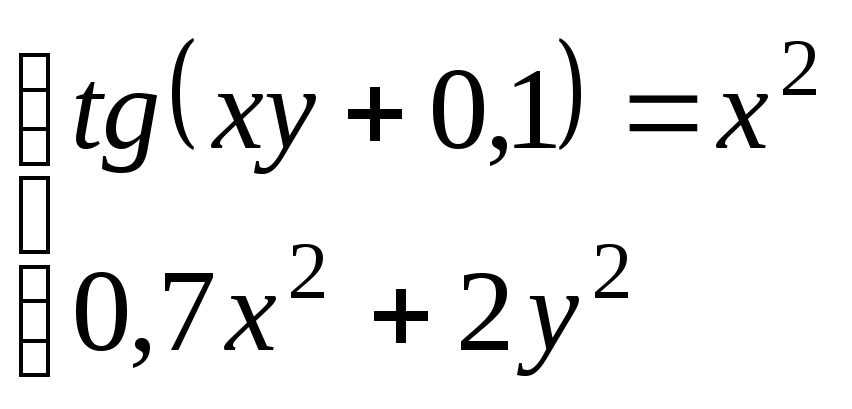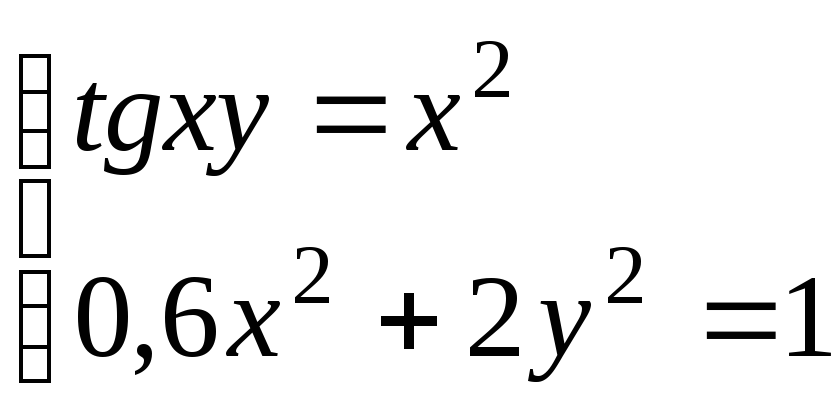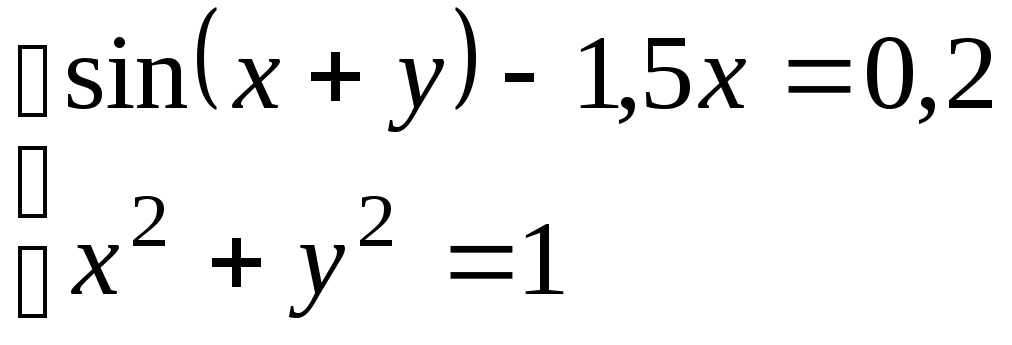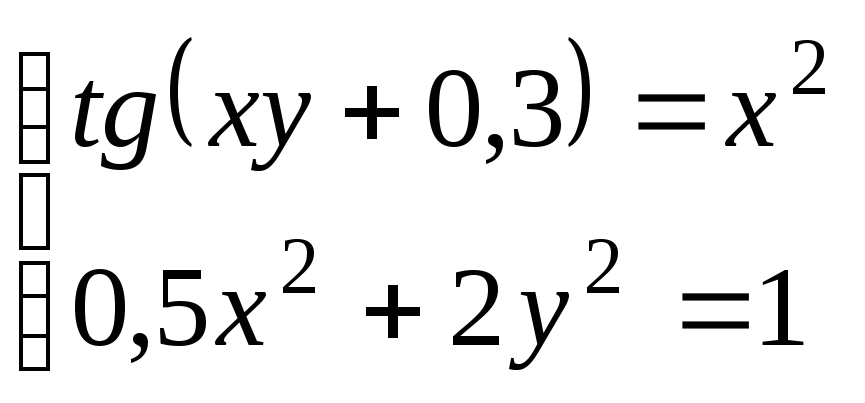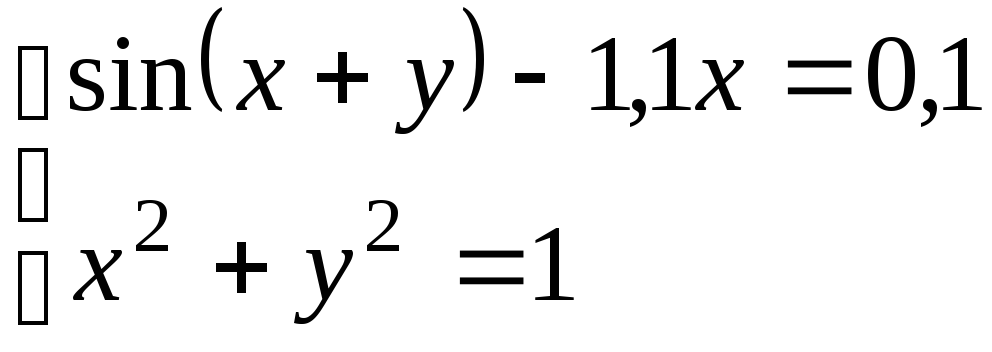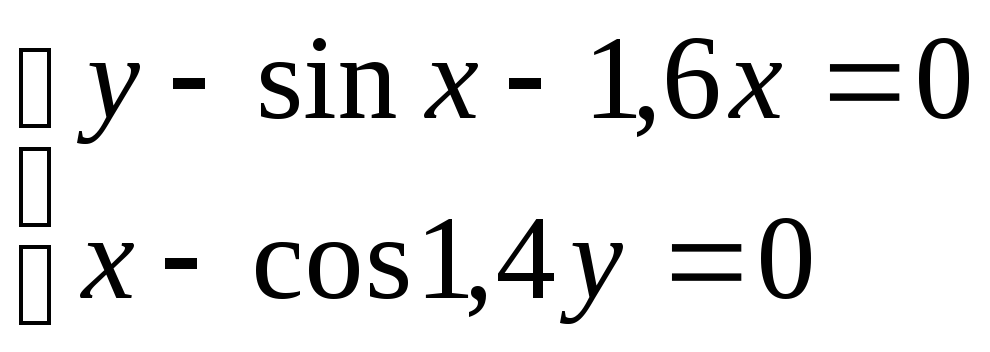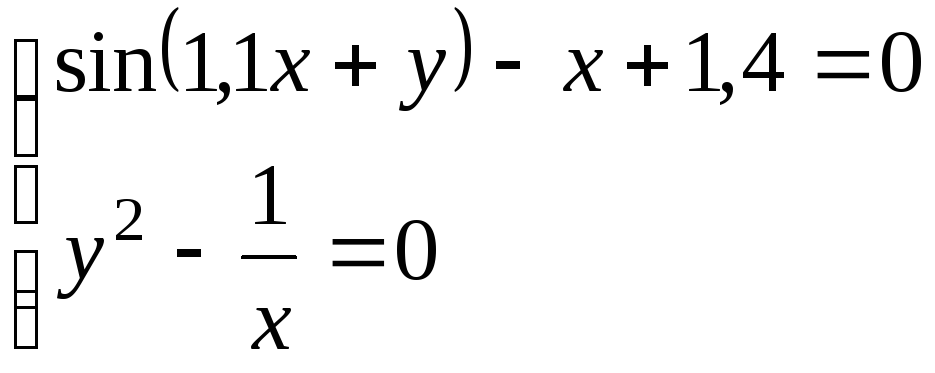Лабораторная работа №1. Приближенное решение алгебраических и трансцендентных уравнений

Задание: Локализовать наименьший положительный корень уравнения и уточнить его значение заданным методом с точностью до

№ варианта	Уравнение	№ варианта	Уравнение
1		26
2		27
3		28
4		29
5		30
6		31
7		32
8		33
9		34
10		35
11		36
12		37
13		38
14		39
15		40
16		41
17		42
18		43
19		44
20		45
21		46
22		47
23		48
24		49
25		50

Вопросы для самоподготовки

1. Что значит найти корень уравнения с точностью ?

2. Каковы этапы приближенного решения нелинейных уравнений? Какова цель каждого этапа?

3. Теорема о существовании и единственности корня на отрезке. Аналитическое и графическое отделение корней.

4. Метод половинного деления (алгоритм, геометрическая иллюстрация, условие окончания вычислений).

5. Метод хорд (алгоритм, геометрическая иллюстрация, условие окончания вычислений).

6. Метод касательных (условия применимости, алгоритм, геометрическая иллюстрация, условие окончания вычислений).

7. Комбинированный метод (условия применимости, алгоритм, геометрическая иллюстрация, условие окончания вычислений).

8. Метод итераций (алгоритм, геометрическая иллюстрация, условие окончания вычислений, достаточное условие сходимости итерационного процесса).

9. Сравнительная оценка методов уточнения корней.

Лабораторная работа №2. Решение систем нелинейных уравнений

Задание: Используя метод Ньютона, решить систему нелинейных уравнений с точностью до .

№ варианта	Система	№ варианта	Система
1		26
2		27
3		28
4		29
5		30
6		31
7		32
8		33
9		34
10		35
11		36
12		37
13		38
14		39
15		40
16		41
17		42
18		43
19		44
20		45
21		46
22		47
23		48
24		49
25		50