Обработка результатов измерений

между крайними значениями ряда вычисляется разность. Называется размахом вероятности или шириной распределения:

R=Xmax-Xmin

R=6,13-(-1,87)=8,00

возможное число разрядов 3≤g≤8:

gmin=0.55*n^0.4=3.47≈3

gmax=1.25*n^0.4=7.88≈8

принимаем число интервалов g=5

определяем ширину интервалов ∆X:

∆X=8\5=1,6

расчет границ интервалов:

∆1=(-1,87; -0,27)

∆2=(-0,27; 1,33)

∆3=(1,33; 2,93)

∆4=(2,93; 4,53)

∆5=(4,53; 6,13)

подсчитываем частоты n_i установив границу интервалов подсчитываем число экспериментальных данных попавших в каждый интервал:

N_i1=8

N_i2=33

N_i3=38

N_i4=18

N_i5=3

расчет середины интервалов:

X_ic=

X1c=(-1,87+(-0,27))\2=-1,07

X2c=(-0,27+1,33)\2=0,53

X3c=(1,33+2,93)\2=2,13

X4c=(2,93+4,53)\2=3,73

X5c=(4,53+6,13)\2=5,33

вычисление среднего арифметического значения измеряемой величины:

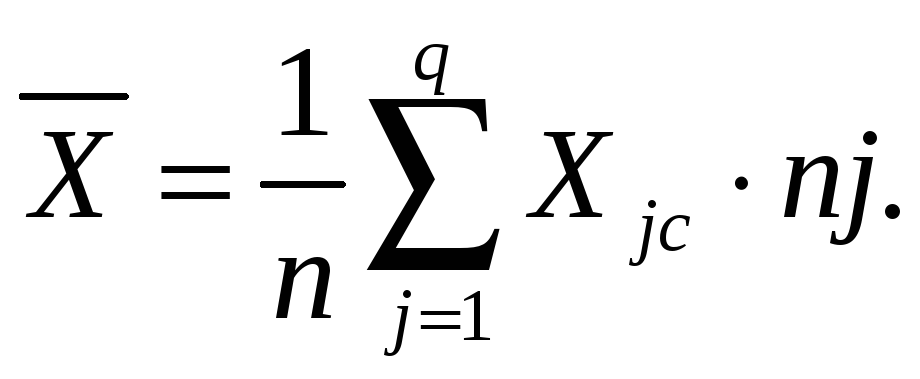
₁₌ -1,07*8=-8,56

₂₌0,53*33=17,49

₃₌2,13*38=80,94

₄₌3,73*18=67,14

₅₌5,33*3=15,99

=0,01*173=1,73

Вычисляются отклонения середин интервалов от среднего арифметического значения и их квадраты: (Хjc – ); (Хjc – )^2:

1. -1,07-1,73= -2,8 5,6

2. 0,53-1,73=-1,2 2,4

3. 2,13-1,73=0.4 0,16

4. 3,73-1,73=2 4

5. 5,33-1,73=3,6 12,96

Определяется произведение квадратов отклонений от среднего на частоту:

(Х_jc –)²·n_j.

1. 5,6*8=44,8

2. 2,4*33=79,2

3. 0,16*38=6,08

4. 4*18=72

5. 12,96*3=38,88

Вычисляется дисперсия и среднее квадратическое отклонение:

D = ;

D=240,96 /99=2,43

σ =√2,43 =1,56

Полученные оценки математического ожидания и СКО является случайными, поэтому рассеивание математического ожидания оценивается с помощью среднего квадратического отклонения среднего арифметического:

=0,156

Таблица 1

Номер раз-ряда	Границы разряда		Середины разрядов Хjc	Частота nj	Хjc· nj	(Хjc –)	(Хjc –)2	(Хjc –)2·nj
1	2	3	4	5	6	7	8	9
1	-1,87	-0,27	-1,07	8	-8,56	-2,8	5,6	44,8
2	-0,27	1,33	0,53	33	17,49	-1,2	2,4	79,2
3	1,33	2,93	2,13	38	80,34	0,4	0,16	6,08
4	2,93	4,53	3,73	18	67,14	2	4	72
5	4,53	6,13	5,33	3	15,99	3,6	12,96	38,88
	—	—	—	100	173	—	—	240,96

Построение статистических графиков

Проверка гипотезы о принятом законе распределения

Таблица 4

Номер разряда	Середины разрядов Хjc	Частота nj	(Хjc –)	Нормиро-ванные середины tj	p(tj)	p(xj)	npj	χ2j
1	2	3	4	5	6	7	8	9
1	-1,07	8	-2,8	-1,79	0,0804	0,051	8,2
2	0,53	33	-1,2	-0,77	0,2966	0,19	30,4	0,22
3	2,13	38	0,4	0,26	0,3857	0,25	40	0,1
4	3,73	18	2	1,28	0,1758	0,11	17,6	0,009
5	5,33	3	3,6	2,31	0,0277	0,02	3,2	—
	–	100	–	–	–	–	–	0,329

3. Для каждого разряда разбиения определяют его центр t_j и подсчитывают число наблюдений , попавших в каждый из интервалов, теоретически соответствующее вы­бранной аналитической модели распределения.

Для этого сначала от реальных середин интервалов переходят к нормированным серединам:

.

1. -2,8\1,56=-1,79

2. -1,2\1,56=-0,77

3. 0,4\1,56=0,26

4. 2\1,56=1,28

5. 3,6\1,56=2,31

рассчитываем плотность вероятности физической величины теоретической функции распределения в единицах этой величины:

_{-0,0804\1,56=0,051}

_{0,2966\1,56=0,19}

_{0,3857\1,56=0,25}

_{0,1758\1,56=0.11}

_{0,0277\1,56=0.02}

,

1,6*100*0.051=8,2

1,6*100*0,19=30,4

1,6*100*0,25=40

1,6*100*0,11=17,6

1,6*100*0.02=3,2

:

1. - - - - - - - - -

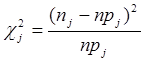2. (33-30,4)^2))\30.4=0,22

3. (38-40)^2))\40=0,1

4. (18-17.6)^2))\17.6=0.009

5. 

Для нахождения граничных значений критерия определяют число степеней сво­боды:

,

Так как , то гипотеза о нормальном распределении принимается.

Проверка гипотезы о принадлежности выборки к генеральной совокупности по критерию согласия Колмогорова

Таблица 7

№ j	Правая граница разрядов Хj+1	Частота nj	Эмпир. частоты Pk	Значен. накопленных частостей эмп. ф-ции распр. (Хj+1 )	Аргумент ф-ции Zj+1	Значен. ф-ции Ф(Zj+1)	Значен. теорет. ф-ции распр. F(Xj+1)	Абсол. велич. разности Hj
1	-0.27	8	0,08	0,08	-1,28	-0,3997	0,1003	0.6997
2	1.33	33	0,33	0,41	-0,26	-0,1026	0,3947	0.0126
3	2.93	38	0,38	0,79	0,77	0,2794	0,7794	0.0106
4	4.53	18	0,18	0,97	1,79	0,4633	0,9633	0.0067
5	6.13	3	0,03	1	2,82	0,4976	0,9979	0.0024

эмпирические частоты

=0,08

=0,33

=0,38

=0,18

=0,03

Значения накопленных частостей

0,08

0,08+0,33=0,41

0,41+0,38=0,79

0,79+0,18=0,97

0,97+0,03=1

Аргумент ф-ции Z_j+1

. Для определения теоретической функции распределения:

а) определяются значения аргумента функции Лапласа, соответствующие правым границам всех интервалов.

z_j+1 = (Х_j+1 –) / σ.

б) определяются значение функции Ф(z_j+1) из таблицы П.4 приложения «Значение функции Ф(Z)»

в) вычисляются значения функции распределения F(X) предполагаемого в качестве теоретического закона распределения

F(Х_j+1 ) = P(Х < Х_j+1 ) = 0,5 + Ф(z_j+1).

1. -2.8\1.56=-1,79

2. -1.2\1.56=-0.77

3. 0,4\1,56=0,26

4. 2\1,56=1,28

5. 3,6\1,56=2,31

Находится абсолютное значение разностей между значениями эмпирической и теоретической функциями распределения при одинаковых значениях аргумента, а затем выбирается наибольшее из них:

H = max | (Х_j+1 ) – F(Х_j+1 ) |.

0,08-0.1003=0.6997

0,41-0.3974=0.0126

0,79-0,7794=0.0106

0,97-0.9633=0.0067

1-0,9976=0.0024

Вычисляется значение λ = H =0,6997*10=6.997

λ α=1,22

ся. Т.к. 1,22 ≤ 6.997 , то выдвинутая гипотеза о принадлежности выборки к генеральной совокупности считается отвергнутой.