2.5.3. Метод вариации произвольных постоянных

Этот метод применим к решению систем неоднородных линейных уравнений. Ограничимся для простоты нормальной системой двух линейных уравнений с постоянными коэффициентами

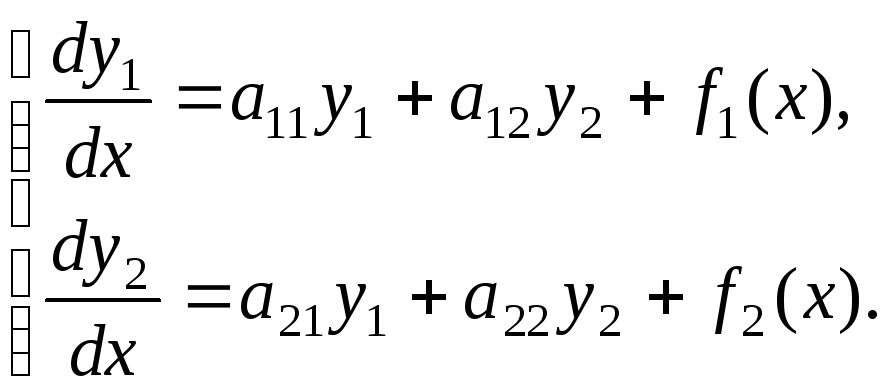(2.113)

Пусть общее решение однородной системы уравнений имеет вид

(2.114)

где ,- произвольные постоянные, а,,,- частные решения однородной системы, соответствующие различным корням характеристического уравнения.

В соответствии с методом вариации частное решение неоднородной системы отыскивается в форме, аналогичной по структуре общему решению однородной системы, но произвольные постоянные в (2.114) заменяются неизвестными функциями, то есть принимается

.

(2.215)

Подстановка (2.115) в (2.113) приводит к следующей системе двух дифференциальных уравнений первого порядка относительно неизвестных функций ,:

 7( 0 C 41 0'(x)y 411 0 + C 42 0'(x)y 412 0 = f 41 0(x),

 7* 0 (2.116)

 79 0 C 41 5' 0(x)y 421 0 + C 42 5' 0(x)y 422 0 = 4  0f 42 0(x).

Разрешая систему (2.116), получим два дифференциальных уравнения первого порядка

f 41 0y 422  0- 4  0f 42 0y 412 0 f 42 0y 411  0- 4  0f 41 0y 421

C 41 5' 0(x) = 4 ------------- 0-- ; C 42 5' 0(x) = 4 ------------- 0--. (2.117)

y 411 0y 422 0 - y 412 0y 421 0 y 411 0y 422 0 - y 412 0y 421

Интегрируя эти уравнения, находим функции C 41 0(x), C 42 0(x) и подставляем их в (2.115). Общее решение системы (2.113) запишется в виде

y 41 0 = 4  0y 41o 0 + y 41*,

y 42  0= 4  0y 42o  0+ 4  0y 42*.

 Пример.  Решить систему

 7( 0 y 5' 0 = -4y 41  0+ y 42 0 + x,

 7* 0  51 0 (2.118)

 79 0 y 5' 0 = -2y 41 0 - y 42 0 + 3x. 2

Общее решение однородной системы, как было показано выше (2.112), имеет вид

y 41o 0 = C 41 0y 411 0 + C 42 0y 412 0 = C 41 0e 5-2x 0 + C 42 0e 5-3x 0,

(2.119)

y 42o 0 = C 41 0y 421 0 + C 42 0y 422 0 = 2C 41 0e 5-2x 0 + C 42 0e 5-3x 0.

Принимаем частное решение системы (2.118) в виде

y 41* 0 = C 41 0(x)e 5-2x 0 + C 42 0(x)e 5-3x 0,

(2.120)

y 42* 0 = 2C 41 0(x)e 5-2x 0 + C 42 0(x)e 5-3x 0.

Подставляя (2.120) в систему (2.118), получим после элементарных преобразований

 7( 0 C 5' 0(x)e 5-2x 0 + C 5' 0(x)e 5-3x  0= x ,

 7* 5 1 2

 79 0 2C 5' 0(x)e 5-2x 0 + C 5' 0(x)e 5-3x 0 = 3x.

 51 2

Решение этой системы приводит к уравнениям

 72 0 x  5  0 e 5-3x 72 0  72 0 e 5-2x 0 x 72

 72 2  0  7 2 2

 72 03x  5  0 e 5-3x 72 0  72 0 2e 5-2x 0 3x 72

C 5' 0(x) = ------------- =2xe 52x 0; C 5' 0(x) = ------------- =-xe 53x 0.

 51 0  72 0 e 5-2x  0 e 5-3x 72 0  5  0  52 0  72 0 e 5-2x  0 e 5-3x 72

 72 2  0  7 2 2

 72 02e 5-2x  0 e 5-3x 72 0  72 02e 5-2x  0 e 5-3x 72

Интегрируя эти уравнения, получим

 7( 0 1 7 )

C 41 0(x) = 2 73 0xe 52x 0dx = e 52x 0  72 0x- -- 7 2 0,

 79 0 2 7 0

e 53x  7( 5 1 7 )

C 42 0(x) = - 73 0xe 53x 0dx = 5  0 ---  72 5 -  0- x 72 0.

3  5  79  03 5  7 0

Поэтому

1 1 5  7( 5 1 7 ) 0 2x 7

y 41* 0 = C 41 0(x)e 5-2x 0 + C 42 0(x)e 5-3x 0 = x- -- + -  72 5 -  0- x 72 0 = --- - -- ,

2 3 5  79  03 5  7 0 0 3 18

 7( 0 1 7 ) 0 1 5  7( 5 1 7 ) 0 5x 8

y 42* 0 = 2C 41 0(x)e 5-2x 0 + C 42 0(x)e 5-3x 0 = 2 72 0x- -- 7 2 0 + -  72 5 -  0- x 72 0 = --- - -.

 79 0 2 7 0 0 3 5  79  03 5  7 0 0 3 9

Общее решение системы запишется в виде

2x 7

y 41 0 = 4  0y 41o 0 + y 41* 0 = C 41 0e 5-2x 0 + C 42 0e 5-3x 0 + --- - -- ,

3 18

5x 8

y 42  0= 4  0y 42o  0+ 4  0y 42* 0 = 2C 41 0e 5-2x 0 + C 42 0e 5-3x 0 + --- - -  4.