3.Операционное исчисление

Операционное исчисление представляет собой своеобразный и эффективный метод решения различных математических задач, прежде всего, дифференциальных уравнений. В основе операционного исчисления лежит понятие преобразования Лапласа.

3.1. Преобразование Лапласа

 Преобразованием Лапласа .  называется преобразование, которое  ставит в соответствие функции f(t) действительной переменной t  функцию F(p) комплексной переменной p по формуле 

(3.1)

Несобственный интеграл в правой части формулы (3 1), зависящий от комплексного параметра p, называется интегралом Лапласа.

Интеграл сходится и действительно определяет собой некоторую функцию F(p), если подынтегральная функция f(t) удовлетворяет следующим условиям:

1) f(t) кусочно - непрерывная функция;

2) f(t) = 0 при t < 0;

3) f(t) по абсолютной величине возрастает не быстрее заранее выбранной показательной функции, то есть можно найти такие постоянные M и  , что

.

Число называется показателем роста функции f(t).

 Функция f(t) действительного аргумента t, удовлетворяющая перечисленным выше трем условиям, называется  оригиналом , а функция F(p) комплексного аргумента p, определяемая согласно ( 3.1),  называется  изображением по Лапласу  функции f(t) или просто  изображением .

Символически соответствие между оригиналом и изображением записывается обычно так:

или .

Совокупность всех оригиналов f(t) называется пространством оригиналов, а совокупность всех изображений F(p) – пространством изображений.

Изображения простейших функций

1. Пусть оригинал имеет вид

 

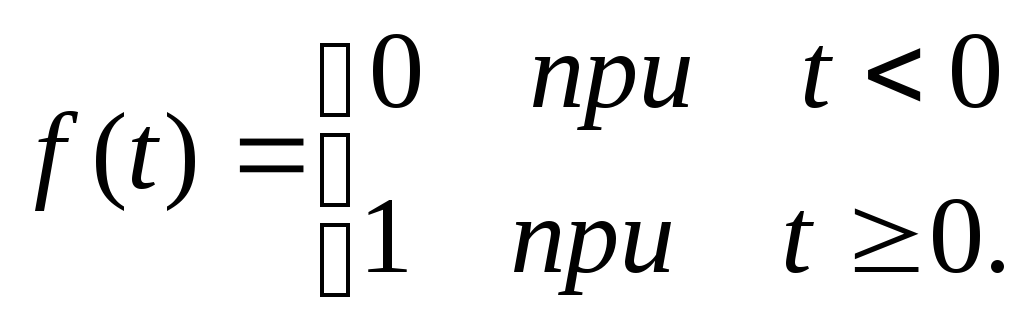
Эта функция широко применяется в приложениях и называется единичной функцией или функцией Хевисайда.

Изображение этой функции найдем по формуле (3.1):

 

.

Следовательно,

. (3.2)

2. Изображение  показательной функции.  Пусть 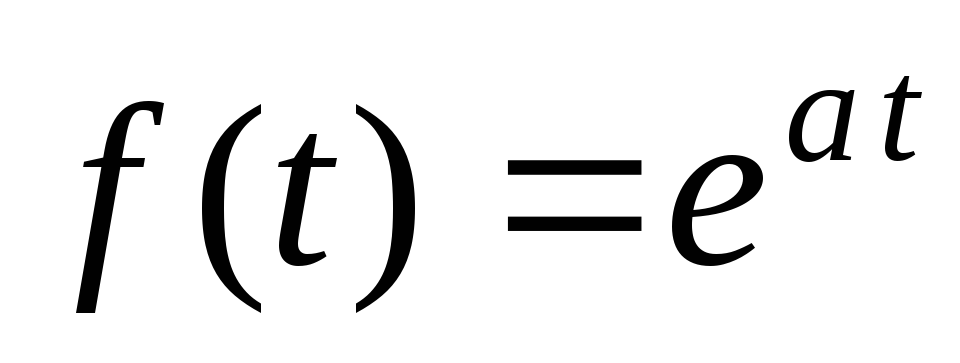 , тогда

 

Следовательно,

. (3.3)

 

Нахождение изображений непосредственно по формуле (3.1) обычно затруднительно. Во многих случаях изображения по Лапласу могут быть найдены значительно проще, если воспользоваться свойствами преобразования Лапласа.

Свойства преобразования Лапласа

Для практического применения преобразования Лапласа необходимо знать не только изображения отдельных функций, но и правила отображения выполняемых над ними операций. Эти правила формулируются в виде многочисленных теорем, объединяемых общим названием "свойства преобразования Лапласа". Рассмотрим некоторые основные из них.

1. Теорема линейности  . Если ,то для любых постоянныхилинейной комбинации оригиналов соответствует такая же линейная комбинация изображений, то есть

  . (3.4)

 Пример.  Найти изображения функций cos t и sin t.

Согласно формулам Эйлера

 

  .

 

Учитывая формулу (3.3) и применяя теорему линейности, получим 

(3.5)

Аналогично

(3.6)

2. Теорема подобия.  Если f(t) = F(p) , то

 

(3.7)

то есть умножение аргумента оригинала на некоторое число a приводит к делению аргумента изображения и самого изображения на то же число ( к подобному изменению изображения ).

 Пример.  Найти изображения функций и. Учитывая изображения (3.5) и (3.6)  и применяя теорему подобия, получим

. (3.8)

Аналогично

. (3.9)

3. Теорема смещения изображения.  Если f(t) = F(p), то для любого числа a (действительного или комплексного)

 

(3.10)

 

то есть умножение оригинала на приводит к смещению аргумента изображения на a.

 Пример. Найти изображения функций и  .

 Учитывая формулы (3.8) и (3.9) и применяя теорему смещения изображения, находим

. (3.11)

Аналогично

  . (3.12)

 

4.Теорема запаздывания. Если f(t) = F(p), то для любого положительного 

. (3.13)

 то есть "включение" оригинала с запаздыванием на время  равносильно

умножению изображения на .

   Пример. Найти изображение функции f(at - b), если f(t) =F(p). Применяя теоремы подобия и запаздывания, получим

 

 В частности,

  (3.14)

. (3.15)

 5. Теорема дифференцирования оригинала.  Если f(t) = F(p), то

, (3.16)

то есть  дифференцирование оригинала сводится к умножению его  изображения на p и вычитанию начального значения функции . В (2.16) - правосторонний предел функции f(t).

(3.17)

…………………………………….

(3.18)

В частности, если все начальные значения функции и ее производных равны нулю, то

(3.19)

Для практических приложений эта теорема является самой важной. Из нее следует, что дифференцирование в пространстве оригиналов заменяется существенно более простой операцией - умножением изображения на степень аргумента. Эта теорема лежит в основе операционного метода решения дифференциальных уравнений.

6.Теорема дифференцирования изображения. Если f(t) = F(p), то

……………………..

.

Учитывая, что и применяя последовательно теорему дифференцирования изображения, найдем изображения степенных функций:

(3.20)

7. Теорема интегрирования оригинала  . Если f(t) = F(p), то

 

. (3.21)

 

Соответствие между некоторыми основными оригиналами и изображениями указано в таблице 4.

Таблица 4

Таблица соответствия