2.4.3. Построение общего решения линейного неоднородного уравнения методом степенных рядов

Пусть требуется найти общее решение линейного неоднородного дифференциального уравнения

(2.74)

Общее решение уравнения имеет вид

(2.75)

где - частное решение неоднородного уравнения,и- постоянные интегрирования,и- частные линейно независимые решения однородного уравнения

. (2.76)

Чтобы построить общее решение уравнения (2.74), будем решать задачу Коши с этим уравнением и начальными условиями:

. (2.77)

Решение задачи (2.74),(2.77) представим рядом

(2.78)

В соответствии с начальными условиями (2.77)

. (2.79)

Для определения последующих коэффициентов ряда подставляем его в уравнение (2.74)

В левой части полученного равенства имеем ряд по степеням x. В правой части - частный случай ряда, у которого все коэффициенты равны нулю, кроме свободного члена, равного 2. Равенство будет тождественно выполняться, если коэффициенты при одинаковых степенях x в левой и правой частях равенства будут соответственно равны между собой. Приравниваем коэффициенты

………………………….

Отсюда получаем рекуррентные соотношения:

…………….

(2.80)

По этим формулам с учётом (2.79) получаем:

и так далее. Подставляя найденные коэффициенты в искомое решение (2.78) и группируя слагаемые, получаем общее решение в форме (2.75)

 

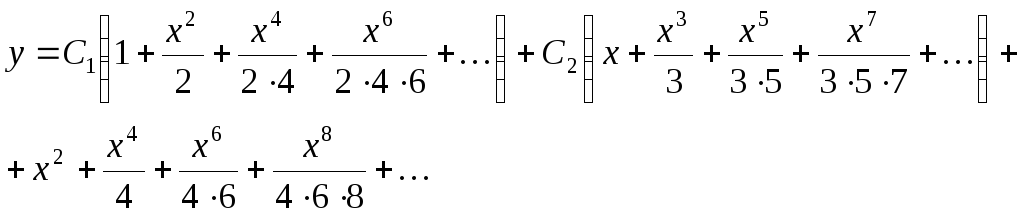
(2.81)

Ряды в (2.81), умноженные на константы и, сходятся на всей числовой оси и определяют функциии ,линейно независимые в окрестности точки x=0. Ряд

также сходится на всей числовой оси и удовлетворяет уравнению (2.74). Поэтому функция является частным решением исходного линейного неоднородного уравнения. Выражение (2.81) представляет общее решение уравнения (2.74). Следует отметить,что частное решениеданного уравнения можно было найти проще путём подбора, принимаяПодставляя функциюв уравнение (2.74), получим. Следовательно,. Тогда функциииследует находить  как частные решения уравнения (2.76), используя рекуррентные соотношения (2.80) и формулы (2.79).