1.3 Оцінка результатів і похибок сумісних та сукупних вимірювань

Загальною ознакою сумісних і сукупних вимірювань, відповідно до їх визначення, є те, що значення шуканих величин отримують як розв’язок системи рівнянь, які пов’язують шукані величини з деякими іншими величинами, вимірюваними прямими або опосередкованими методами. Причому вимірюють декілька комбінацій значень цих величин. Вимірювання, проведені для кожної комбінації, дозволяють одержати одне рівняння, а сукупність цих рівнянь для всіх комбінацій являє собою систему рівнянь, в яку входять також усі значення шуканих величин [58].

При сукупних та сумісних вимірюваннях невідомі величини х_і , що підлягають безпосередньому вимірюванню, визначають за результатами вимірювання інших величин, які функціонально пов'язані з ними

φ(х₁, х₂,..., х_п) = y_j, (1.75)

де і = 1,2,.., п - порядковий номер невідомих величин х; j = 1,2,.. , m - порядковий номер прямих вимірювань величин у .

Якщо результати прямих вимірювань Y містять випадкові похибки, то вони мають місце і в результатах сукупних (сумісних) вимірювань величин х_i. Розглянемо три випадки.

1 .Очевидно, що для т < п систему розв'язати неможливо.

2.Для т = п розв'язання можливе, але похибки результатів вимірювання величин х_i будуть, як і для прямих одноразових вимірювань, значними, і числові значення цих похибок залишаються невідомими.

З.Для т > п систему знову неможливо розв'язати алгебрично, оскільки ці рівняння несумісні, так як праві частини рівнянь замість точних значень Y_i містять результати їхніх вимірювань у_i = Y_i + ΔΥ_i із випадковими похибками ΔΥ_i.

Проте в останньому випадку для нормального закону розподілу похибок вимірювання величини у_i можна знайти таку сукупність значень х, яка з найбільшою ймовірністю задовільняла б початкові умови φ(x₁ ,х₂ ,...,х_п ) = у_i . Це можна здійснити за допомогою методу найменших квадратів (принципу Лежандра).

Такий спосіб обробки експериментальних даних для сукупних (сумісних) вимірювань доцільно застосовувати для лінійних функцій. В інших випадках обробка результатів значно ускладнюється.

Тому розглянемо випадок, коли функції φ_j лінійні

(1.76)

Представимо систему більш компактно:

. (1.77)

Тут індекси при коефіцієнтах а показані у послідовності «рядок-стовпець».

Ці рівняння називають умовними. Через наявність похибок праві частини рівнянь дорівнюють не нулю, а деяким залишковим похибкам:

. (1.78)

Згідно з принципом Лежандра, найбільш імовірними значеннями невідо­мих величин х_i для цього випадку будуть такі, для яких сума квадратів залишкових похибок мінімальна

. (1.79)

Необхідною умовою такого мінімуму повинна бути рівність нулю похідних

і = 1, 2, ..., n. (1.80)

Підставивши в останню формулу значення v_i, отримують систему нормальних рівнянь

h = 1, 2, …, n, (1.81)

яку в розгорнутому вигляді представляють наступним чином

(1.82)

Індекси при коефіцієнтах b показані в послідовності «рядок-стовпець» (h - і).

Оскільки кількість нормальних рівнянь завжди дорівнює кількості невідомих, то така система має розв'язок.

Методика отримання системи нормальних рівнянь полягає у знаходженні часткових похибок від кожної v_j по кожній з невідомих х_i шляхом перемноженням цих похідних на відповідні значення v_j та додаванні їх для кожної невідомої х_і

(1.83)

Сукупність даних виразів представляє собою систему з п нормальних рівнянь.

Визначемо нормальні рівняння для n = 2.

Припустимо, що в результаті сукупних (сумісних) вимірювань отримано систему

(1.84)

Система нормальних рівнянь матиме вигляд:

(1.85)

Коефіцієнти b_hi визначають з виразів

b₁₁ = ; b₁₂ = b₂₁ = ; b₂₂ =

Тоді значення c_h визначають

c₁ = c₂ =

Розв’язок системи нормальних рівнянь проводиться наступним чином.

Якщо кількість невідомих п ≤ 4, то систему нормальних рівнянь доцільно розв'язувати за допомогою визначників. Розглянемо розв'язок систем нормальних рівнянь для п = 2 .

У цьому випадку складаємо та обчислюємо головний визначник цієї системи рівнянь

D = (1.86)

Далі складаємо та обчислюємо часткові визначники D₁ та D₂, замінивши коефіцієнти b при відповідних невідомих на вільні члени с в системі

D₁ = , D₂ = .

Знаходимо найбільш імовірні значення невідомих

Середні квадратичні значення результатів сукупних (сумісних) вимірювань. Після підстановки найбільш імовірних значень х до умовних рівнянь

, j = 1, 2, …, m, знаходимо значення залишкових похибок v_j, визначаємо v та суму квадратів залишкових похибок .

Середнє квадратичне відхилення результатів сукупних (сумісних) знаходять за формулою

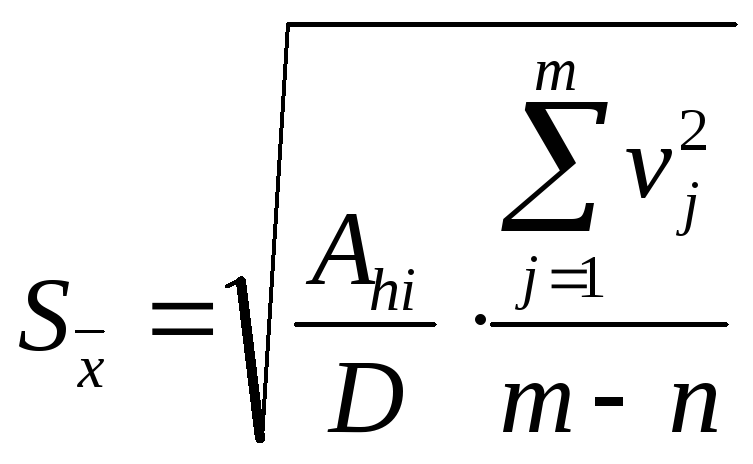, (1.87)

де т - кількість умовних рівнянь; п - кількість невідомих; А_hi - ад'юнкти (алгебричні доповнення) елементів b_hi головної діагоналі визначника D (для h = і), які отримують викресленням h -го рядка та і -го стовпця, відповідних даному елементу b_hi , з наступним домноженям на (—1)^h+1.

Для п = 2 ад'юнкти: А₁₁ = b₂₂ , А₂₂ = b₁₁.

Довірчі границі випадкової складової похибки сукупних (сумісних) вимірювань. Задавшись значенням довірчої ймовірності, знаходимо відповідне значення коефіцієнта довіри t_р. У цьому випадку число ступенів вільності дорівнює:

k = m – n ; (1.88)

Довірчі границі випадкової похибки сукупних (сумісних) вимірювань становлять:

Δі = ± tр∙ S (1.89)