Питання для самоперевірки

1. Які критерії називаються параметричними?

2. Як перевіряється гіпотеза про середнє значення з відомим СКВ?

3. Як перевіряється гіпотеза про середнє значення з невідомим СКВ?

4. Як перевіряється гіпотеза про дисперсії?

5. Як перевіряється гіпотеза про наявність зсуву?

6. Як обчислюється ймовірність помилки першого роду?

7. Як обчислюється ймовірність помилки другого роду?

8. Що характеризує параметр А при визначенні необхідного обсягу випробувань?

9. Як обчислюється необхідний обсяг випробувань?

2.3 Параметричні критерії розбіжностей для двох сукупностей. Критерії Фішера і Кохрена

Параметричні критерії можна застосовувати при визначенні розбіжності параметрів розподілу сукупностей.

Порівняння двох середніх. Завдання такого плану трапляються тоді, коли необхідно переконатися в тому, чим викликана розбіжність середніх, отриманих на підставі наявних двох вибірок з однієї генеральної сукупності випадкових величин X і Y обсягами n₁ і n₂. Іншими словами, чи зумовлена ця розбіжність впливом випадкових величин і обмеженим обсягом вибірки або ж справді існує розбіжність між центрами розподілів (систематичними похибками приладів, продуктивністю праці, довговічністю, надійністю тощо).

Для випадку з відомим СКВ генеральних сукупностей.

Відомі σ_x і σ_y величин X і Y. Висуваємо гіпотезу H₀: v_х=v_y при альтернативній H₁: v_х ≠ v_y. Необхідно визначити, чи істотна розбіж­ність між середніми і , отриманими відповідно з вибірки обся­гом п₁ для випадкової величини Хі обсягом п₂ для випадкової вели­чини Y.

Позначимо

Розглянемо різницю и як параметр Z, тобто у вигляді нормованої різниці

де а при висунутій гіпотезі

Величини Хі Y — незалежні величини, для яких тому можна записати

(2.7)

Для перевірки правильності гіпотези використовують двобічну критичну область. З урахуванням виразу (16.1) значення статистич­ної характеристики

Значення z порівнюють із критичним значенням Якщо приймають гіпотезу Н₀.

Для випадку з невідомими СКВ генеральних сукупностей. У цьому разі визначають емпіричне значення s і використовують статистичну характеристику

розподілену за законом Стьюдента.

Відомо, що для незалежних випадкових величин

За умови, що вибірки взято з однієї генеральної сукупності, тобто можна записати

або

_(2.8)

Зважаючи на те, що вибірки взято з однієї генеральної сукупності, доцільно скористатися всіма наявними експериментальними даними, тобто розглядати вибірку обсягом п₁ + п₂. Це дає змогу підвищити статистичну надійність знайденої оцінки СКВ генеральної сукупності. Тоді

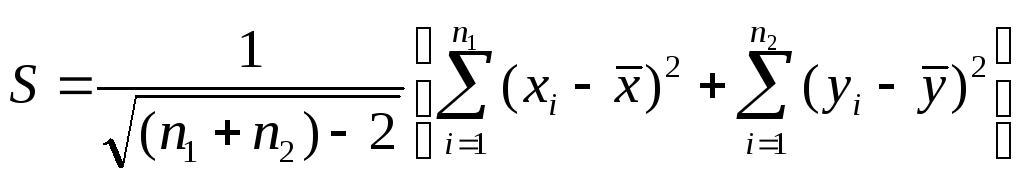(2.9)

Виходячи з виразу для дисперсії, можна записати:

Аналогічно маємо:

Підставляють отримані значення сум у вираз (2.9) і дістають:

(2.10)

Підставляють вираз (2.10) у вираз (2.8) і отримують

(2.11)

З урахуванням виразу (2.11) розрахункове значення коефіцієнта Стьюдента буде

Для перевірки гіпотези необхідно знайти критичне значення ко­ефіцієнта Стьюдента t_кр Для заданого рівня статистичної значущості α і кількості ступенів свободи п₁ + п₂.- 2. Якщо розрахункове зна­чення |t_р| ≤ t_кр, приймають нульову гіпотезу.

У випадку, коли вибірки взято не з однієї генеральної сукупності, тобто для визначення суттєвості розбіжності обчислених середніх і коефіцієнт Стьюдента обчислюють за формулою:

Обчислене значення порівнюють із критичним значенням коефіцієнта Стьюдента, яке залежно від α і кількості ступенів свободи обчислюють за формулою

де

Порівняння двох дисперсій. Другою важливою ознакою, за якою можуть порівнюватися дві сукупності, є дисперсії в кожній із них. Гіпотези про дисперсії відіграють важливу роль у техніці, оскільки са­ме дисперсія характеризує такі важливі конструкторські й технологічні показники, як точність приладу, похибку результату, точність техноло­гічного процесу тощо.

При спільній обробці результатів необхідно, насамперед, пере­конатися в тому, що умови проведення дослідів, при яких отримані результати, були однаковими. З цією метою можна використати оцінку розбіжності дисперсій.

F-критерій (розподіл Фішера). Припустимо, що задано дві генеральні сукупності X та Y з нормальним розподілом X N (µ₁, σ₁) і Y N (µ₂, σ₂). Із цих генеральних сукупностей зроблено незалежні вибірки з параметрами відповідно п₁, , п₂,. Потрібно при рівні значущості α перевірити гіпотезу при альтернативній гіпотезі.

Математик-статистик Р. Фішер установив, що відношення незсунених оцінок двох дисперсій підпорядковується закономірності, що залежить від кількості ступенів свободи цих дисперсій. Припускаючи, що, приймають як статистику величину F, котра задовольняє F-розподіл, для якого з кількістю ступенів свободи, що дорівнює п₁ – 1 і п₂ – 1 відповідно.

Критична область буде тільки правобічна і визначається умовою .

Значення знаходять із таблиць F-розподілу, яке залежить від трьох величин: рівня значущості α і двох чисел, якими виражаються ступені свободи . Таблиці складені окремо для кожного значення α (тривимірні таблиці). Задаючись рівнем статистичної значущості α, вибравши в таблиці колонку і рядок , на їх перетині знаходять критичне значення коефіцієнта .

Якщо можна стверджувати на підставі наявних експериментальних даних, що при рівні статистичної значущості а вибіркові дисперсії будуть однорідні.

Іноді перед обробкою даних необхідно переконатися в однорідності дисперсій, отриманих на підставі даних двох експериментальних ви­бірок. У цьому випадку також використовується критерій Фішера.

Відмінністю є те, що альтернативна гіпотеза . Для пе­ревірки гіпотези використовують двобічну критичну область (рис. 2.8), тобто передбачається, що ймовірність того, що розрахункове значення буде меншим за критичне значення або більшим за не перевищує значення

Оскільки в таблиці є тільки значення , то значення можна знайти безпосередньо з таблиць.

Рис. 2.8

Для визначення , яке відповідає умові , вводять коефіцієнт

Тоді

Останнє співвідношення показує, що можна знайти виходячи з умови . Надалі перевірка залишається такою самою, як і для однобічної критичної області, тобто нуль-гіпотеза, приймається в тому випадку, коли розрахункові значення містяться між критичними й .

Перевірка гіпотези про однорідність ряду дисперсій. (G-критерій). Якщо потрібно побудувати аналітичну залежність (аналітичну модель) на основі експериментальних даних, то на­самперед необхідно переконатися в однорідності вибіркових дис­персій. Для цього серед наявних вибіркових дисперсій вибирають максимальну, а потім розглядають відношення максимальної ди­сперсії до суми всіх вибіркових дисперсій. Для випадку, коли об­сяги вибірок однакові, тобто в кожній вибірці дисперсія обчис­лювалася на підставі однакової кількості даних m, застосовують G-критерій (критерій Кохрена). Статистика G вказує, яку частку має максимальна дисперсія в загальній дисперсії, і обчислюється за формулою:

де — дисперсія для кожної i-ї вибірки, і=1,

Висувають гіпотезу Н₀: дисперсії однорідні. Для перевірки ну­льової гіпотези знайдене розрахункове значення G_р порівнюють із критичним значенням коефіцієнта G_кр, яке знаходять із таб­лиць критичних значень G-критерію на перетині стовпця та рядка для заданого рівня статистичної зна­чущості α.

Якщо на підставі наявних даних можна стверджувати, що вибіркові дисперсії будуть однорідні, тобто гіпотеза Н₀ приймається.

Якщо гіпотеза про рівність дисперсій відхиляється, то збільшують обсяг вибірок і знову перевіряють гіпотезу. Якщо ж гіпотеза знову не підтверджується, такі вибіркові дані спільно обробляти не можна