Додаток а

1 Структура мережі зв'язку

1.1. Основні поняття теорії графів

Теорія графів є розділом математики, що має широкі практичні додатки. Багато проблем, що виникають в таких вельми різних областях знань, як психологія, управління, планування, хімія, електроніка, торгівля, освіта і ін., можуть бути сформульовані як задачі теорії графів. Зважаючи на це теорія графів цікава не тільки сама по собі, але також і тим, що представляє загальну основу, на якій результати, одержані в різних областях знань, можуть бути зібрані, узагальнені і поширені.

На відміну від інших наукових дисциплін, теорія графів має цілком певну дату народження. Перша робота по теорії графів, написана математиком Леонардом Ейлером, була опублікована в 1736 р. в працях Академії наук в Санкт-Петербурзі. Ним була сформульована і розв’язана задача про Кенігсбергські мости [3].

До 50-х років нашого століття в теорії графів склалися два цілком різних напрями: алгебраїчний і оптимізаційний. Останній одержав широкий розвиток завдяки появі ЕОМ і у зв'язку з розробкою методів лінійного програмування. У даному навчальному посібнику розглядатимемо оптимізаційний напрям теорії графів.

Граф G задається безліччю точок або вершин х₁, х₂, ..., х_n (які позначимо X) і безліччю ліній або ребер (гілок) а₁, а₂, ...,а_m (які позначимо А), об’єднуючих між собою всі або частину цих точок. Таким чином, граф G повністю задається парою (X, А), тобто G =(X, А) [4]. Замість позначень X і А можна використовувати і інші.

Якщо ребра з множини А орієнтовані, що звичайно показується стрілкою, то граф називається орієнтованим графом, або орграфом. Ребра орграфа звичайно називають дугами. Орграф приведений на рис. 1.1. Якщо ребра не мають орієнтації, то граф називається неорієнтованим (рисунок 1.2). Граф, що має як орієнтовані так і неорієнтовані ребра, називається змішаним (рис. 1.3). Якщо в графі між двома якими-небудь вершинами є декілька ребер, то такий граф називається мультиграфом (рис. 1.4).

Рисунок 1.1 – Зображення орграфа

Рисунок 1.2 – Зображення неорієнтованого графа

Рисунок 1.3 – Зображення змішаного графа

Рисунок 1.4 – Зображення мультиграфа

Зазвичай вершинам графа приписуються номери (або позначення x_i, x_j ) щоб розрізняти їх і мати нагоду ними оперувати в процесі аналізу. Ребра графа позначаються звичайно а = (x_i, x_j), де x_i, x_j - початкова і кінцева вершини, зв'язані даним ребром. Окрім цього позначення, застосовують також a(x_i, x_j), або а(i, j), або а _{i j.} Іноді ребро (дугу) позначають (i, j).

У використовуваних позначеннях i, j - номери вершин. Крім того, ребра можна позначати а_i, де i - номер ребра.

Шляхом µ _{i j} графа називається послідовність ребер, що починається у вершині i, закінчується у вершині j, у якій кінцева вершина кожного ребра, відмінного від останнього, є початковою вершиною наступного.

Так, на рис. 1.5 послідовності дуг а₆, а₅, а₉, а₈, а₄; а₁, а₆, а₅, а₉ є шляхами. Ці послідовності можна також записати у формі:

а(х_2, х₅), а(х₅, x₄), а(х₄, х₃), а(x₃, х₅), а(х₅, х₆);

а(х₁, х₂), а(х₂, х₅), а{х₅, х₄), а(х₄, х₃).

Більш простішою є наступна форма запису:

а₂₅, а₅₄, а₄₃, а₃₅, а₅₆;

а₁₂, а₂₅, а₅₄, а₄₃.

Шлях називається простим, або само непересічним, якщо в ньому не повторюються ні вершини, ні ребра.

У розглянутому прикладі другий шлях є простим.

Цикл - це шлях, початкова і кінцева вершини якого співпадають.

Граф називається зв'язковим, якщо для будь-яких різних вершин існує, принаймні, один сполучаючий їх шлях.

У орграфе шлях називають також ланцюгом.

Нагадаємо, що граф - це безліч вершин і ребер, позначається G = (X, А). Будь-яка підмножина множини G називається підграфом, позначається =(,).

Дерево графа визначається як зв'язна підмножина , що не містить циклів. Отже, для будь-яких двох вершин графа в дереві існує єдиний шлях, що сполучає їх.

У графі, що містить n вершин, підграф із k вершин (k ≤ n) є деревом, якщо виконані будь-які дві з наступних умов:

1) підграф є зв'язковим,

2) підграф не має циклів,

3) число ребер в підграфі рівне k - 1.

Рисунок 1.5 – Зображення послідовності дуг а₆, а₅, а₉, а₈, а₄; а₁, а₆, а₅, а₉ , що

є шляхами

Рисунок 1.6 – Зображення графа

Остовним деревом, або остовом, називається дерево, що містить всі вершини графа. Отже, якщо граф містить n вершин, то дерево з n вершинами і n - 1 ребром є остовом. Дерево для графа (рис. 1.6) представлене на рис. 1.7, остовне дерево - на рис. 1.8. Тут для спрощення вершини графа позначені номерами, гілки ж не позначені. Їх позначатимемо при необхідності.

Помітно, що для графа можна побудувати декілька остовних дерев.

Надалі для спрощення, якщо це не обумовлено особо, остовне дерево називатимемо просто деревом.

Рисунок 1.7 – Зображення дерева графа для графа (рис. 1.6)

Рисунок 1.8 – Зображення остовного дерева для графа (рис.1.6)

Якщо для вказівки деяких звичайних обмежень, що накладаються на ребра (дуги) графа, зіставити останнім числа, які називаються вагами ребер, або їх кількісними характеристиками, відповідними, наприклад, відстані, вартості, часу або іншим адитивним величинам, то можна ввести поняття мінімального (або максимального ) дерева. Вага дерева визначається як сума вагів його ребер (звідси і вимога до адитивності характеристик ребер графа).

Найкоротшим (максимальним) деревом називається дерево з мінімальною (максимальною) вагою. Іноді таке дерево називають деревом мінімальної (максимальної) вартості.

Рисунок 1.9 – Зображення дерева графа рис. 1.5

Рисунок 1.10 – Зображення остова графа рис. 1.5

Дерева і остови визначаються як для орієнтованих, так і для неорієнтованих графів.

На рис. 1.9 зображено дерево графа рис. 1.5, на рисунку 1.10 - остов графа рис. 1.5.

Січенням (розрізом) графа називається сукупність ребер, при видаленні яких граф розпадається на два незв'язні підграфи.

Перетин σ_st, що розділяє вершини s і t, є безліч ребер (А, ), де s є А , t є . Число С (А, ) називається пропускною спроможністю (величиною) січення. Пропускна спроможність січення визначається як сума пропускних спроможностей ребер, утворюючих січення. На графах січення звичайно позначається лініями, що пересікають ребра, утворюючих січення.

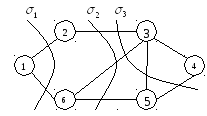
Рисунок 1.11 – Розподіл графа на підграфи січеннями σ_1, σ_2, σ₃

На рис. 1.11 січення σ₁ включає ребра (1, 2), (1, 6) і розділяє граф на два підграфи, в одному з яких вершина 1, в іншому - вся решта вершин і ребер. Січення σ₂ (ребра (2, 3), (6, 3), (6, 5)) розділяє граф на два підграфи, в одному з яких вершини 1, 2, 6 і ребра (1, 2), (1, 6), в іншому - вершини 3, 4, 5 і ребра (3, 4), (3, 5) і (4, 5). Січення σ₃ розділяє граф на два підграфи, в одному з яких вершини 1, 2, 5, 6 і ребра (1, 2), (1, 6),(6, 5), в іншому - вершини 3 і 4 і ребро (3, 4).