
Міністерство транспорту та зв’язку України
УКРАЇНСЬКА НАЦІОНАЛЬНА АКАДЕМІЯ ЗВ’ЯЗКУ ім. О. С. Попова
ННІ Економіки та менеджменту
Кафедра Управління проектами та системного аналізу
ЗАВДАННЯ ТА МЕТОДИЧНІ ВКАЗІВКИ
до виконання комплексного завдання
з курсу
„ЕКОНОМЕТРІЯ”
для студентів усіх форм навчання
(Спеціальностей: 7.050107, 7.050201)
ЗАТВЕРДЖЕНО
методичною радою академії
Протокол №
від
Одеса 2009
УДК План НМВ 2009 р.
Укладачі: Бобровнича Н.С.
Жуковська Л.Е.
Рецензент – доц. Горелкіна С.Б.
Методичні вказівки містять завдання та список літератури для виконання комплексного завдання з курсу „Економетрія”.
Рекомендовано студентам усіх форм навчання вищих навчальних закладів I-IV рівнів акредитування які навчаються за спеціальностями 7.05107 та 7.050201.
УХВАЛЕНО
на засіданні кафедри
Управління проектами та системного аналізу
і рекомендовано до друку
Протокол № 10
від 27.05. 2009 р.
ВСТУП
Метою курсу „Економетрія” є вивчення основ економіко-математичного моделювання й застосування математичних моделей при розв’язанні завдань планування й управління зв'язку.
Вивчення даного курсу вимагає попередньої підготовки студентів з дисциплін:
-
вища математика, розділи «Лінійна алгебра», «Булева алгебра»;
-
обчислювальні методи, розд. «Лінійне програмування».
Дисципліна вивчається студентами усіх форм навчання. З дисципліни читаються лекції, виконуються практичні заняття, проводяться консультації.
Для оцінки знань студентів з дисципліни передбачається виконання комплексного завдання. Номер виконуваного варіанта визначається двома останніми цифрами номера студентського квитка. Кожна задача комплексного завдання містить методичні вказівки щодо її виконання й посилання на літературу.
Список рекомендованої літератури
-
Барсук В. А., Губкин Н. М., Батый А. Р. Экономико-математические методы и модели в планировании и управлении в отрасли связи. – М. : Радио и связь, 1984. – 264 с.
-
Корольов О. А. Економетрія.– Київ, 2000. – 659 с.
-
Магнус Я. Р. Економетрика – М. : Дело, 2004. – 575 с.
-
Лук’яненко І., Красникова Л. Економетрика. – Київ: Знання, 1998. – 493 с.
Комплексне завдання
Подані задачі комплексного завдання охоплюють основні розділи курсу “Економетрія” і сприяють більш глибокому розумінню матеріалу, який вивчається.
Розв’язки задач слід розташовувати в порядку їхніх номерів. Комплексне завдання слід виконувати в окремому зошиті, заповнюючи при цьому лише один бік аркуша. Зворотний бік залишається для можливих зауважень рецензента і внесення відповідних виправлень.
Розв’язки задач повинні бути чіткими, пояснення короткими, але без скорочення слів. У разі потреби слід робити посилання на літературу з указівкою номерів формул, рисунків і таблиць. Рисунки слід виконувати акуратно, за допомогою лінійки.
Комплексні роботи, виконані недбало, без проміжних обчислень, із пропуском задач або не за заданим варіантом, не враховуються і повертаються для доопрацювання.
Задачі комплексного завдання, вихідні дані.
Задача 1. Для заданого варіант мережі рис.2. треба скласти структурну матрицю В і за допомогою бульових визначників знайти множину шляхів mij від вузла i до вузла j та множину шляхів mst від вузла s до вузла t. Значення і, j, s та t подано в таблиці 1.
Варіант структури мережі визначається останньою цифрою номера студентського квитка, варіант значень i, j, s та t визначається передостанньою цифрою номера студентського квитка.
Таблиця 1
|
Цифра десятків |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
0 |
|
i j s t |
1 2 2 4 |
1 3 2 5 |
1 4 3 4 |
1 5 3 5 |
2 3 4 5 |
2 4 2 3 |
2 5 1 5 |
3 4 1 3 |
3 5 1 4 |
4 5 1 2 |
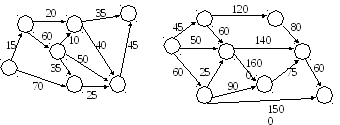
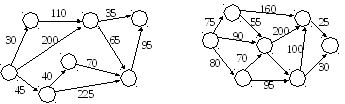
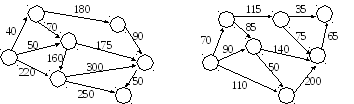
Задача 2. Визначити шлях мінімальної ваги й мінімального рангу поміж кожними двома вузлами мережі за допомогою мережного й матричного методів.
Вихідні дані обираються за останньою цифрою студентського квитка для мережного метода з табл. 2 та рис. 1, а для матричного – з табл. 3. та рис. 3.
Таблиця 2 – Вихідні дані для мережного методу
|
Остання цифра студентського квитка |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
0 |
|
Номер вузла витоку |
17 |
1 |
6 |
9 |
2 |
7 |
5 |
10 |
3 |
4 |
|
Номер вузла стоку |
3 |
14 |
18 |
13 |
18 |
15 |
17 |
13 |
10 |
16 |

Рисунок 1 – Заданий граф
Таблиця 3 – Вихідні дані для матричного методу
|
Варіант 1 |
|
Варіант 2 |
|
Варіант 3 |
||||||||||||||||
|
|
|
1 |
2 |
3 |
4 |
5 |
|
|
1 |
2 |
3 |
4 |
5 |
|
|
1 |
2 |
3 |
4 |
5 |
|
|
1 |
0 |
20 |
30 |
|
15 |
|
1 |
0 |
15 |
|
40 |
|
|
1 |
0 |
|
25 |
60 |
|
|
|
2 |
20 |
0 |
50 |
40 |
|
|
2 |
15 |
0 |
25 |
30 |
50 |
|
2 |
|
0 |
30 |
40 |
|
|
|
3 |
30 |
50 |
0 |
|
25 |
|
3 |
|
25 |
0 |
35 |
60 |
|
3 |
25 |
30 |
0 |
|
15 |
|
|
4 |
|
40 |
|
0 |
60 |
|
4 |
40 |
30 |
35 |
0 |
45 |
|
4 |
60 |
40 |
|
0 |
50 |
|
|
5 |
15 |
|
25 |
60 |
0 |
|
5 |
|
50 |
60 |
45 |
0 |
|
5 |
|
|
15 |
50 |
0 |
-
Варіант 4
Варіант 5
1
2
3
4
5
1
2
3
4
5
1
0
25

60

1
0
30

40

2
25
0
50
40
30
2
30
0
45

25

3

50
0
45


3

45
0
50
90
4
60
40
45
0
35
4
40

50
0
70
5

30

35
0
5

25
90
70
0
-
Варіант 6
Варіант 7
1
2
3
4
5
1
2
3
4
5
1
0
25
50
60

1
0
50
60
30

2
25
0
40

60
2
50
0
40

15

3
50
40
0
15
100
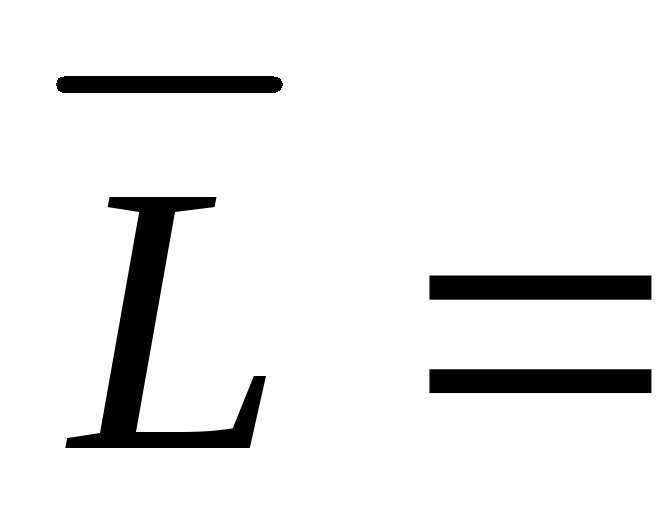
3
60
40
0

60
4
60

15
0
30
4
30


0
100
5

80
100
30
0
5

15
60
1000
0
|
Варіант 8 |
|
Варіант 9 |
|
Варіант 10 |
||||||||||||||||
|
|
|
1 |
2 |
3 |
4 |
5 |
|
|
1 |
2 |
3 |
4 |
5 |
|
|
1 |
2 |
3 |
4 |
5 |
|
|
1 |
0 |
30 |
40 |
50 |
25 |
|
1 |
0 |
70 |
30 |
50 |
|
|
1 |
0 |
15 |
30 |
|
|
|
|
2 |
30 |
0 |
75 |
|
15 |
|
2 |
70 |
0 |
|
25 |
60 |
|
2 |
15 |
0 |
|
60 |
35 |
|
|
3 |
40 |
70 |
0 |
45 |
|
|
3 |
30 |
|
0 |
45 |
80 |
|
3 |
30 |
|
0 |
55 |
40 |
|
|
4 |
50 |
|
45 |
0 |
|
|
4 |
50 |
25 |
45 |
0 |
30 |
|
4 |
|
60 |
55 |
0 |
|
|
|
5 |
25 |
15 |
|
|
0 |
|
5 |
|
60 |
|
30 |
0 |
|
5 |
|
35 |
40 |
|
0 |
Задача 3. Для заданого варіанта мережного графіка (МГ), поданого на рис. 3, з тривалостями робіт, зазначеними на МГ, визначити параметри:
Тр(і), Тп(і) – ранній та пізній терміни здійснення подій;
Тр п(і, j), Тп п(і, j) – ранній та пізній терміни початку робіт;
Тр з(і, j), Тп з(і, j) – ранній та пізній терміни завершення робіт;
Ri, Ri, j, ri, j – резерви часу подій, загальні та окремі резерви робіт.
Номер варіанта МГ визначається передостанньою цифрою номера студентського квитка.
1 2 a

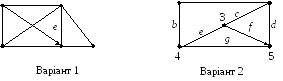
1 a

Рисунок 2 – Варіанти структур мереж зв’язку
Варіант 1 Варіант 2

Варіант 3 Варіант 4

Варіант 5 Варіант 6
Варіант 7 Варіант 8
Рисунок 3 – Варіанти мережних графіків
Варіант 9 Варіант 0
Рисунок 3 – Закінчення варіантів мережних графіків
Задача 4. Для заданого варіанта мережі ( рис. 4) треба скласти матрицю найкоротших відстаней Lопт = Д і маршрутну матрицю Г, яка визначальну вершини графа, складові шляхи (необхідно використовувати алгоритм Флойда).








 20
40
20
40
 10
15 15
30 25 18
10
15 15
30 25 18

















 15 20
25 20
14
15 20
25 20
14
40 10 12 20


 12
15 15
10
12
15 15
10
20 35


В аріант
1 Варіант
2
аріант
1 Варіант
2









 25
40
25
40





 15 15 20
10 25
25 35 10
15 15 20
10 25
25 35 10




 30
30
 10
35 20
20 33
10
35 20
20 33







25 10 20 10 15 18 22 25




 25
40
25
40


Варіант 3 Варіант 4





 21
25
21
25







 8 10
14 13 5
14 27 16
8 10
14 13 5
14 27 16






 7
18 10
8 23
7
18 10
8 23








6 15 22 14 9 16 12 14




 30
21
30
21


Варіант 5 Варіант 6









 12
16
12
16





14 11 9 8 15 27 23 8




 15
14
15
14







 12
16 30
35
12
16 30
35



16 21 13 43 47



 12
20
21
12
20
21
20 50
Варіант 7 Варіант 8







 18
18
18
18



21 18 16 15 25 21 27 14












 42
28 16
15
42
28 16
15
 31
28
31
28
27 19 23 16 21 14 35





 41
40
41
40
Варіант 9 Варіант 0
Рисунок 4 – Варіанти для метода Флойда
