
- •Понятие лса. Общие подходы к проектированию
- •Требования, предъявляемые локальным сетям
- •Вид потребляемой энергии Аналоговые локальные системы
- •Математические модели объектов управления
- •Методы линеаризации уравнений
- •Мм нелинейных элементов
- •Общий метод описания эквивалентных передаточных функций нэ
- •Гармоническая линеаризация типовых нелинейных элементов
- •Двузначная нелинейность
- •Для двухзначной нелинейности
- •Статическая линеаризация существенных нелинейных элементов
- •Совместная гармоническая и статическая линеаризация
- •Логарифмические эквивалентные амплитудные и фазовые характеристики сложных нелинейных элементов
- •Статическая линеаризация существенных дискретных нелинейных элементов
- •Вычислительные процедуры для определения коэффициента гармонической и статической линеаризации нелинейных элементов
- •Математическая модель сар
- •Управляемость и наблюдаемость
- •Анализ локальных систем управления
- •Качество
- •Построение переходных процессов с помощью вещественных или мнимых частных характеристик
- •Построение переходных процессов с помощью импульсных переходных систем
- •Исследование динамической точности
- •Коэффициенты ошибок
- •Определение характеристик точности и дискретно-непрерывных лса
- •Синтез лса
- •Синтез линейных непрерывных локальных систем заданных структур
- •Синтез дискретно непрерывных систем
- •Последовательное программирование
- •Параллельное программирование
- •Синтез линейных непрерывных локальных систем
- •Постановка задачи синтеза частотными методами
- •Выбор параметров неизменяемой части
- •Выбор типа двигателя для регулируемого органа
- •Электрические двигатели
- •Гидравлические двигатели
- •Проверка правильности выбора механической передачи
- •Синтез последовательных и параллельных корректирующих устройств
- •Подстановка задачи и выбора универсальной эвм
- •Примеры синтеза систем комбинированного типа
- •Сенсорные устройства. Датчики роботов.
- •Позиционные лсу
- •Контурные лсу
Логарифмические эквивалентные амплитудные и фазовые характеристики сложных нелинейных элементов
Для подавления автоколебаний или распределения областей устойчивых состояний в некоторых типах нелинейных систем применяют сложные нелинейные элементы, представляющие собой сумму параллельно нелинейных или последовательных соединений нелинейностей, разъединенных линейным звеном и линейных элементов, образующих внутренние контуры с отрицательной и положительно обратной связью.
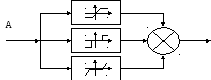
Рисунок 31
Для получения логарифмических и фазовых характеристик сложных нелинейных характеристик используются шаблоны характеристик каждого элемента, по которым строится суммарная характеристика.

Рисунок 32
Статическая линеаризация существенных дискретных нелинейных элементов
Квантование по времени в ЛСА осуществляется импульсными устройствами на основе трех типов модуляции: АИМ, ШИМ, ЧИМ. Быстродействующие устройства с АИМ являются линейными импульсными элементами, а устройства с ШИМ и ЧИМ – нелинейными.
Нелинейный импульсный элемент для удобства математического описания можно представить в виде совокупности линейного и нелинейного элемента. Сигнал на выходе с двухзначного нелинейного элемента записывается в виде:
![]() ,
(126)
,
(126)
где
![]() .
(127)
.
(127)
При этом будем считать, что входной сигнал является гармоническим, то есть
![]() ,
(128)
,
(128)
где
![]() ;
(129)
;
(129)
![]() - полупериод
гармонического колебания, (
- полупериод
гармонического колебания, (![]() ).
).
 .
(130)
.
(130)
При учете первой гармоники, выходной сигнал будет равен:
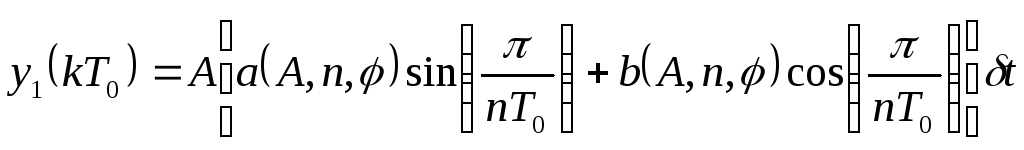 ,
(131)
,
(131)
Определим условие
наилучшего квадратичного приближения
![]() к
к![]() для этого запишем соотношение:
для этого запишем соотношение:
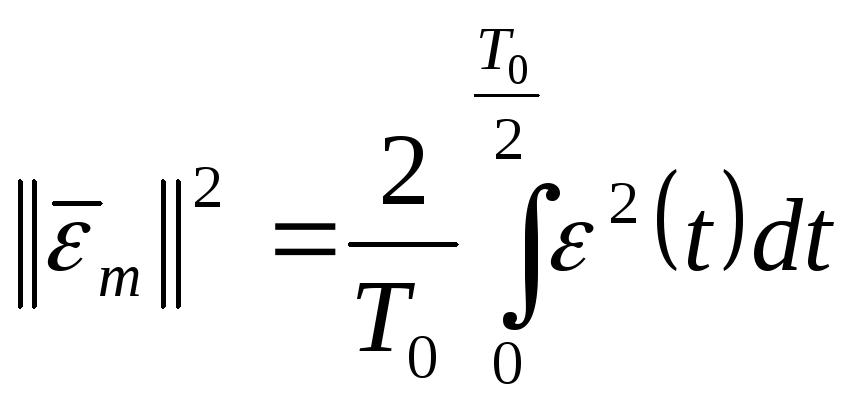 ,
(132)
,
(132)
где
![]() - полупериод функции
- полупериод функции![]() .
.
 .
(133)
.
(133)
После преобразования получим
 ,
(134)
,
(134)
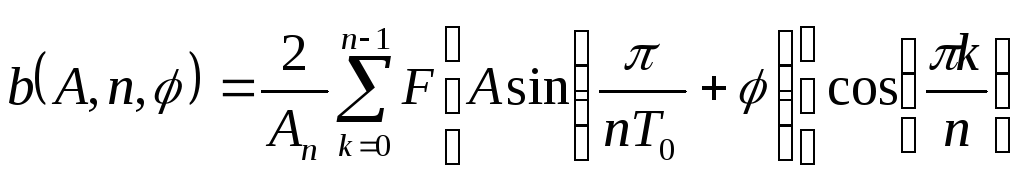 .
(135)
.
(135)
Пользуясь этими двумя формулами, найдем эквивалентную передаточную функцию.
![]() ,
(136)
,
(136)
где
![]() ,
(137)
,
(137)
![]() .
(138)
.
(138)
Вычислительные процедуры для определения коэффициента гармонической и статической линеаризации нелинейных элементов
Для сложных видов дискретных нелинейностей довольно трудно получить формулы, позволяющие вычислить коэффициент гармонической и статической линеаризации. В этом случае можно рекомендовать пользоваться программами, составленными на языке ПЛ/1 для различных численных процедур интегрирования. Так, например, программа TRP, предназначенная для вычисления коэффициентов в гармонической неоднозначной нечетно-симметричной нелинейности методом трапеции.
