Двузначная нелинейность

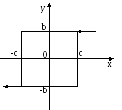
Рисунок 24

Рисунок 25

Рисунок 26

Рисунок 27

, (89)

, (90)

,

, (91)

, (92)

, (93)

, (94)

при ,

, (95)

, (96)

.

С помощью шаблонов находят амплитуды и частоты автоколебаний в нелинейных системах и строим области устойчивых и неустойчивых состояний по параметрам линейной и нелинейной части.

Существует два типа двухзначных нелинейностей: пассивные и активные.

Под пассивными – понимается такие двузначные нелинейности, которые за один период входного сигнала нелинейная характеристика обходится против часовой стрелки. В этом случае в выходном сигнале наблюдается фазовое запаздывание. Если обход нелинейной характеристики проходит по часовой стрелке, то двузначная нелинейность является активной и в выходном сигнале имеет место фазовое опережение. Активные нелинейности применяют в устройствах коррекции СА для обеспечения устойчивости. Реализация таких устройств может быть выполнена на электронных элементах или в виде рабочей программы.

Рассмотрим гармоническую линеаризацию нелинейности, когда на их вход поступает сигнал вида:

, (97)

где - постоянная составляющая основного сигнала.

, (98)

- функция смещения входного сигнала;

- коэффициент гармонической линеаризации.

. (99)

Рисунок 28

,

, (101)

при - для однозначной нелинейности со смещением.

Для двухзначной нелинейности

Рисунок 29

, (102)

, (103)

. (104)

В нелинейных системах при недостаточном уровне подавления линейной части высших гармоник, необходимо учитывать дополнительные гармонические составляющие – автоколебания. При этом эквивалентная передаточная функция зависит от двух сигналов: частотного или многочастотного сигналов. Использование таких передаточных функций в нелинейных системах целесообразно, если требуется оценить влияние высших гармоник на появление автоколебаний.

Например: если в системе на первой гармонике открывают автоколебания, а действие третей появится.

Пусть на вход двузначной нечетной нелинейности поступает сигнал:

, (106)

где - сдвиг фазы третьей гармоник.

Тогда на выходе

. (107)

Пусть ,

, (108)

где и- коэффициенты линеаризации по первой и третьей гармонике.

. (109)