Мм нелинейных элементов

Рассмотренные в первой главе методы линеаризации применимы, когда нелинейность, входящая в объект ЛСА, хотя бы один раз дифференцируема или аппроксимируется касательной с малой погрешностью некоторой окрестности близкой к рабочей точке. Существует целый класс нелинейностей, для которых оба условия не выполняются. Обычно это существенные нелинейности. К ним относятся: ступенчатые, кусочно-линейные и многозначные функции с точками разрыва первого рода, а также степенные и транстендентые функции. Использование УВМ, обеспечивающих выполнение логико-алгебраических операций в системах привело к новым типам линейностей, которые представляют через непрерывные переменные с помощью специальной логики.

Для математического описания таких нелинейностей применяют эквивалентные передаточные функции, зависящие от коэффициентов линеаризации, которые получают путем минимизации среднего квадрата ошибки воспроизведения заданного входного сигнала. Форма входных сигналов, поступающих на вход нелинейностей может быть произвольна. На практике наиболее распространение получили гармонические и случайные виды входных сигналов и их временные комбинации. Соответственно и методы линеаризации называются гармоническими и статическими.

Общий метод описания эквивалентных передаточных функций нэ

Весь класс существенных нелинейностей разделены на две группы. К первой группе относится однозначные нелинейности, у которых связь между входными и выходнымивекторными сигналами зависит только от формы статической характеристики нелинейности.

. (41)

Рисунок 15

В этом случае, при определенной форме входных сигналов:

. (42)

С помощью матрицы линеаризации можно найти приближенное значение выходных сигналов:

. (43)

Из (42) следует, что матрица коэффициентов линеаризации однозначных нелинейностей, является действительными величинами и их эквивалентные передаточные функции:

. (44)

Ко второй группе относят двузначные (многозначные) нелинейности, у которых связь между входными и выходными сигналами зависит не только от формы статической характеристики, но так же определяется предысторией входного сигнала. В этом случае выражение (42) запишется в виде:

. (45)

Рисунок 16 – Двузначная нелинейность

Для учета влияния предыстории входного периодического сигнала будем учитывать не только сам сигнал , но и скорость его изменения, дифференциал.

При входных сигналах:

приближенное значение входного сигнала будет:

, (46)

где и- коэффициенты гармонической линеаризации двухзначных нелинейностей;

- период колебания по правой гармонике;

- гармоническая функция.

Эквивалентная передаточная функция:

. (47)

Существуют нелинейности более общего вида:

, (48)

, (49)

где и- коэффициенты гармонической линеаризации;

- номер гармоники.

Матрицы коэффициентов линеаризации периодической с периодом . Имея это ввиду, передаточную функцию двух двухзначной нелинейности (48) можно представить по аналогии с передаточной функцией (47).

. (50)

Пользуясь (44), (46) и (49) определим обобщенную формулу для вычисления передаточной функции однозначных и двухзначных нелинейностей.

В случае однозначной нелинейности матрица коэффициентов линеаризации , зависящей от параметров вектора, выберем, таким образом, чтобы линеаризовать среднее значение квадрата разности между точными приближеннымсигналами на входе:

, (51)

где «черта сверху» - это силовое усреднение.

. (52)

После преобразований, упрощений, ухищрений и усиления бдительности, получим эквивалентную передаточную функцию в виде системы матриц: ,.

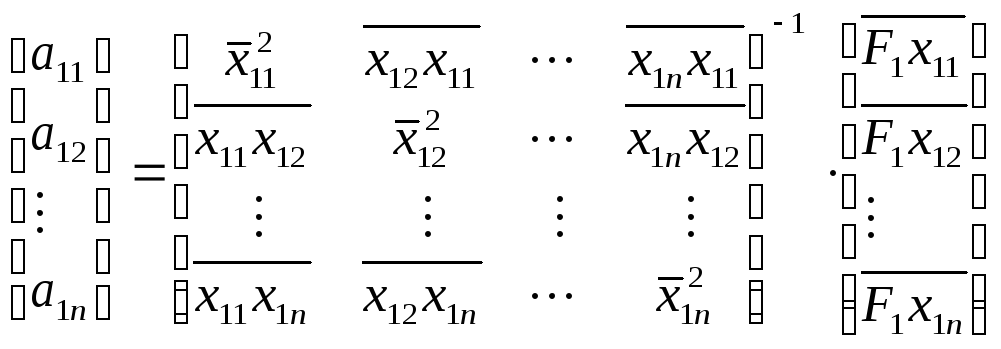, (53)

при ,.

. (54)

Пример.

Определить коэффициент линеаризации для однозначной нелинейности. Когда на ее вход поступает первая гармоника синусоидального сигнала:

, (55)

где .

. (56)

Уравнение (56) представляет собой коэффициент линеаризации по первой гармонике для однозначной нелинейности, она определяет эквивалентную передаточную функцию .

В дальнейшем сравнение формулы для определения коэффициентов линеаризации простейших нелинейностей при подаче на их вход периодических сигналов: синусоидального, треугольного, покажем целесообразность применения получаемых эквивалентных передаточных функций.

Перейдем к распределению обобщенного метода описания коэффициентов линеаризации на двухзначные нелинейности.

В этом случае, учитывая соотношение (50) и (52), можно записать:

, (57)

Уравнение (52) примет вид

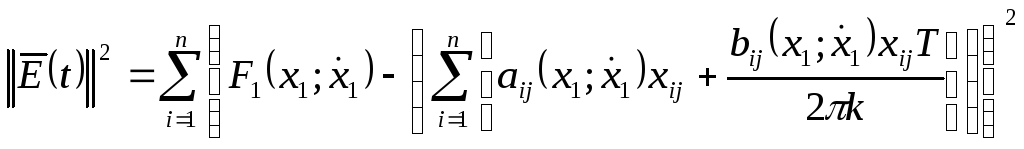. (58)

Коэффициент линеаризации определим (58) ,.

, (59)

. (60)

Пример. Определить коэффициент линеаризации двузначной нелинейности, когда на ее вход поступает первая гармоника синусоидального сигнала и имеет один вход. Из системы матриц (60), получим:

, (61)

. (62)

В данном примере входной сигнал запишем в виде:

, (63)

, (64)

. (65)

Когда для двузначной нелинейности общая эквивалентная функция:

. (66)