Лекция №16

Цель лекции: Изучить способы поиска градиента адаптивных систем.

Задачи лекции:

1. Способ производной по времени.

2. Способ запоминания экстремума.

3. Способ Гаусса-Зайделя.

4. Способ градиента.

5. Способ наискорейшего спуска.

Желаемый результат:

Студенты должны знать:

1. Способ производной по времени.

2. Способ запоминания экстремума.

3. Способ Гаусса-Зайделя.

4. Способ градиента.

5. Способ наискорейшего спуска.

Учебный материал

Способ производной по времени

Производная по функции времени определяется выражением:

(1)

Из выражения (1) следует, что, задавая поочерёдно скорости изменения y₁, y₂, …y_n и производную по времени , можно найти составляющие градиенты.

Недостатком этого метода является необходимость дифференцирования функции F по времени, что сопровождается поднятием уровня высокочастотных помех.

Способ запоминания экстремума

Этот способ заключается в том, что система совершает вынужденное или автоколебательное движение в зоне экстремума.

При достижении экстремального значения F=F_э, оно фиксируется на запоминающем устройстве. Градиент функции определяется по разности текущего и экстремального значения.

Способ Гаусса-Зайделя

Способ заключается в поочерёдном изменении координат y₁, y₂, …y_n. Сначала фиксируются координаты с y₂ до y_n, а координата y₁ изменяется так, чтобы соответствующая градиента стала =0:

Затем фиксируются все координаты от y₃ до y_n :

и так далее

до

После этого возвращаются к началу и повторяют весь цикл снова.

Этот процесс продолжается до тех пор, пока не будет получена точка экстремума.

Способ градиента

В этом способе осуществляется одновременное изменение всех координат так, чтобы обеспечить движение системы в направлении близком к мгновенному направлению вектора градиента.

В простейшем случае непрерывного безынерционного управления должны быть реализованы следующие зависимости:

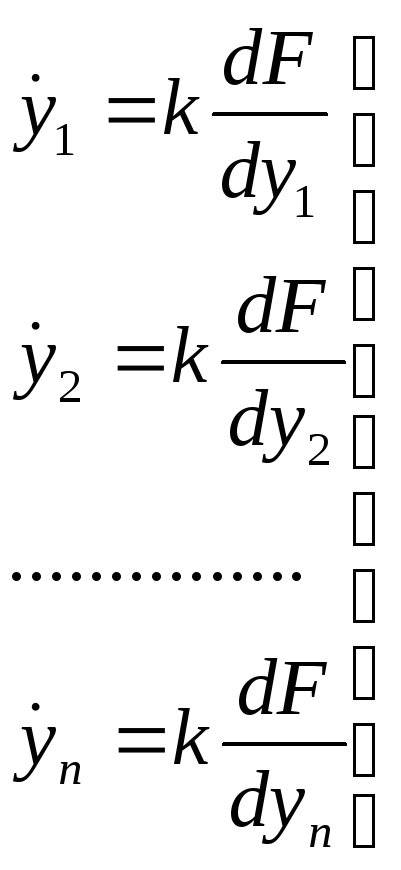(2)

Здесь k – коэффициент пропорциональности.

Для получения правильного направления движения для случая экстремума максимума – k>0, экстремума минимума – k<0.

Уравнение (2) соответствует устойчивому движению экстремальной системы, при котором производная от F сохраняет свой знак всюду, кроме точки экстремума.

При шаговом движении:

(3)

, , …– фиксированные шаги в направлении экстремумам.

Способ наискорейшего спуска

При способе наискорейшего спуска движение происходит по начальному направлению вектора градиента до тех пор, пока производная функция F по этому направлению не обратится в нуль. Затем опять определяется направление градиента и происходит движение вдоль этого вектора до обращения в нуль производной от F по этому направлению. Процесс повторяется до достижения точки экстремума.

Рассмотрим схему экстремального регулирования настройки колебательного контура.

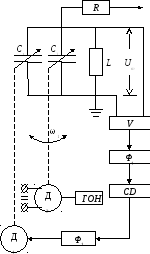
Общая ёмкость колебательного контура:

с=с₁+с₂+с₂₀+Аsinω₁t (4)

Здесь с₂₀ – постоянная составляющая ёмкости конденсатора с₂,

ω₁ – угловая частота вращения ротора.

ω₁ выбирается так, чтобы она была во много раз меньше частоты полезного сигнала ω=2πf и больше возможной частоты процесса регулирования.

Двигатель Д₂ синхронно с вращением конденсатора ротора с₂ даёт опорную величину и в виде опорного напряжения той же частоты от генератора ГОН.

Переменное напряжение на колебательном контуре после выпрямления и сглаживания фильтром F₁ поступает на вход синхронного детектора. На выходе синхронного детектора формируется сигнал, пропорциональный производной от амплитуды напряжения контура по ёмкости .

Этот сигнал после сглаживания фильтром F₂ поступает далее на усилитель и двигатель Д₁. последний будет изменять регулируемую величину и производить подстройку до тех пор, пока производная не станет =0.

Всякое изменение частоты сигнала будет вызывать автоматическую подстройку на максимум напряжения на контуре.

В рассматриваемой экстремальной системе получается своеобразная следящая система, ошибкой которой является производная , поэтому эта схема может быть приведена к соответствующей структурной схеме:

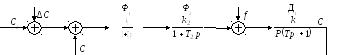
Входной величиной является значение ёмкости, соответствующее экстремуму. Оно связано соотношением , гдеL – индуктивность.

Результирующая передаточная функция разомкнутой системы имеет вид:

Исследование динамики исследуемой системы сводится к исследованию следящей системы. Поэтому здесь применимы все методы, используемые в непрерывных автоматических системах.

Помимо обычных показателей качества для экстремальных систем используется ещё одна характеристика – потери на поиск. В установившемся режиме регулируемая величина колеблется около значения, соответствующего экстремуму функции. В следствии этого, среднее значение отличается от экстремального. Среднее значение, обусловленное колебаниями поиска в установившемся режиме работы системы, называется потерями на поиск и представляется в виде степенного ряда:

(5)

В степенном ряду частная производная соответствует точке экстремума, а Δу – это отклонение от этой точки. Если использовать квадратичную форму, то потери на поиск можно представить в виде:

Здесь – средний квадрат отклонения регулируемой величины соответствующего экстремума.

Если известна амплитуда поиска А₁, то:

И в общем случае:

(1)

Рассмотрим исследование динамики экстремальной системы при F=F(y₁, y₂, …y_n) для случая поиска экстремума по способу градиента.

Структурная схема исследования динамики экстремальной системы

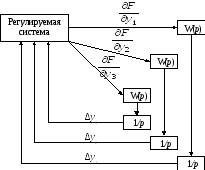
Эта схема имеет:

или

W(p) – одинаковая для всех каналов.

Для малых отклонений для точки экстремума:

(2)

(3)

В n-мерном пространстве:

(4)

Т.е. область экстремума минимума является эллипсоидом.

Если (5)

(5) – эллипсоид экстремума максимума.

(6)

(6) – уравнение для малых отклонений.

С_i – полуоси определяющего эллипсоида.

"+" – минимум

"-" – максимум

(7)

(7) – характеристическое уравнение для каждого из каналов.

Таким образом, исследование динамики сводится к анализу n-изолированных каналов, которым соответствуют характеристические уравнения (7).

Вопросы самоконтроля:

1. Способ производной по времени.

2. Способ запоминания экстремума.

3. Способ Гаусса-Зайделя.

4. Способ градиента.

5. Способ наискорейшего спуска.