
Лекции / леккции
.pdfЛЕКЦИИ ПО «ЛОКАЛЬНЫМ СИСТЕМАХ УПРАВЛЕНИЯ»
1

ЛЕКЦИЯ №1 Цель лекции: Изучить определение локальных систем управления; рассмот-
реть классификацию локальных систем автоматического управления; рассмотреть общие требования к локальным системам управления.
Задачи лекции:
1.Предмет дисциплины локальные системы управления.
2.Классификация локальных систем управления.
3.Общие требования к локальным системам управления.
Желаемый результат:
Студенты должны знать:
1.Определение локальной системы автоматического управления;
2.Классификация локальных систем автоматического управления;
3.Общие требования к локальным системам управления.
Учебный материал. Общие понятия ЛСУ
ЛСУ – это система управления для решения одной функциональной задачи, для управления одним устройством, для регулирования или сигнализации одного параметра.
Классификация ЛС
|
|
|
|
|
|
|
|
|
ЛСУ |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Аналоговые |
|
|
|
|
Дискретные |
|
|
|
Комбинированные |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Механические |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Аналого- |
|
|
|
|
С жесткой ло- |
|
|
|
Программно- |
|
|||||||||||
|
|
|
|
|
|
|
|
дискретные |
|
|||||||||
|
|
|
|
гикой |
|
|
|
|
|
управляемые |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Пневматические |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дискретно- |
|
||
|
|
|
|
|
|
|
Электронные |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
аналоговые |
|
||||||||
|
Гидравлические |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
Пневматические |
|
|
Аналого- |
|
|||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
Электрические |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
дискретно- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
аналоговые |
|
||
|
|
|
|
|
|
|
|
|
Электро- |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Электронные |
|
|
|
|
механические |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
Дискретно- |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Электро-пневмо- |
|
|
|
аналого- |
|
||||||
|
Комбинированные |
|
|
|
|
|
|
дискретные |
|
|||||||||
|
|
|
|
|
гидравлические |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Общие требования к ЛС
1.Энергоѐмкость.
2.Вид потребляемой энергии.
3.Надѐжность работы.
4.Быстродействие.
2
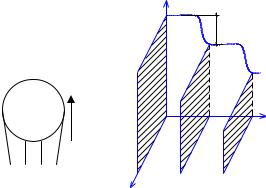
5.Точность поддержания регулируемого параметра (не более 20%).
6.Вид системы (дискретная – человек управляет).
7.Элементная база.
8.Влияние внешних возмущений.
9.Дизайн.
Пример по энергоёмкости:
|
h |
|
|
hmax |
|
|
|
h1 |
h |
0 |
t |
|
|
t1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mc |
|
m |
cg |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m g |
||||||||||||||||||||
Это одностороннее регулирование |
|||||||||||||||||||||||||||
Nш |
|
m0c gh |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где Nш – работа шара. |
|||||||||||||||||||||||||||
h |
|
|
Nш |
– быстродействие одностороннего регулирования. |
|||||||||||||||||||||||
t |
m g |
|
|||||||||||||||||||||||||
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Вывод: быстродействие одностороннего регулирования будет тем больше, чем менее инерционен объѐкт.
Если необходимо поддерживать высокую точность регулирования, то объект должен быть максимально инерционным.
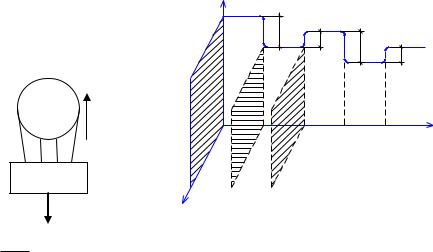
Рассмотрим процесс двустороннего регулирования:
3
|
|
h |
|
|
|
|
|
|
|
hmax |
|
|
|
|
|
|
|
|
|
h1 |
|
|
|
|
|
|
|
|
h2 |
h3 |
|
|
|
|
|
|
|
h4 |
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
0 |
t1 |
t2 |
t3 |
t4 |
t |
mcg |
mc |
|
|
|
|
|
|
(мешки с |
(пассажиры) |
(m p + m c )g |
|
|
|
|
|
песком) |
|
m g |
|
|
|
|
|
m Nш .
t gh
Выводы:
1)двустороннее управление любой координаты объекта управления около начального уровня только при наличии избыточной или скрытой энергии, т.е. еѐ запасов;
2)регулирование любой координаты объекта управления возможно только в пределах ниже, максимально допустимых, т.е. управлять объектам управления по любой координате можно только при условии, что объект управления не требует большей координаты, чем та, которой обладает регулятор;
3)для быстрого управления необходима мощность. Слабомощный регулятор быстро управлять не может;
4)для управления надо использовать усилительные эффекты, т.е. мощность и энергию самого ОУ.
Вопросы самоконтроля:
1.Дать определение локальных систем автоматического управления.
2.Перечислить все виды локальных систем управления.
3.Перечислить общие требования, предъявляемые к локальным системам управления.
4.Дать определение одностороннему управлению координатой объекта управления.
5.Дать определение двухстороннему управлению координатой объекта управления.
ЛЕКЦИЯ №2 Цель лекции: Изучить математическое описание локальных систем управле-
ния; рассмотреть примеры математического описания объекта управления на примере.
Задачи лекции:
1.Математические модели объекта управления ЛСУ.
2.Примеры математических моделей объекта управления ЛСУ.
3.Математические модели дискретных объектов управления ЛСУ.
Желаемый результат:
Студенты должны знать:
4
1.Определение переменных состояния локальной системы автоматического управления;
2.Математическое описание дискретных объектов ЛСУ.
Учебный материал Математические модели ОУ
Наиболее часто для математического описания используются дифференциальные, интегрально-дифференциальные и разностные уравнения, записанные по координатам или в векторно-матричной форме.
Динамические элементы относятся к непрерывным, если рассматриваемые процессы и сигналы изменяются непрерывно.
В дискретных элементах процессы и сигналы имеют конечное число значений по величине и времени.
Математические описания элементов удобно выполнять через переменные состояния. Они аналогичны обобщѐнным координатам, а пространство их изме-
нений является фазовым. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
у(t) – переменное состояние; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
x(t) – входящие сигналы; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
u(t) – выходящие сигналы. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
y t |
f |
y t ,u t , t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1) |
|
|
|
|
|
|
|
|
|
x t g y t ,u t , t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
y1 |
t |
u1 |
t |
|
x1 |
t |
|
f1 |
|
|
g1 |
|
|||||||||||
|
y |
|
t |
u |
t |
|
x |
|
t |
|
f |
|
|
|
g |
|
|
|||||||
y t |
|
|
2 |
|
|
2 |
|
|
x t |
|
|
2 |
|
|
f y t , u t , t |
|
|
2 |
|
g y t , u t , t |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
. |
|
u t |
. |
|
|
|
|
. |
|
. |
|
. |
|
|||||||||
|
|
y |
. |
|
|
. |
|
|
|
x |
|
. |
|
|
. |
|
|
. |
|
|||||
|
|
|
t |
u |
t |
|
|
|
t |
|
|
f |
|
|
|
|
g |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
n |
|
|
n |
|
|
|
n |
|
|
|
n |
|
|
n |
|
||||||
(1) позволяет описать
(1) справедлива в заданном интервале времени (t0, t) и при заданных начальных и граничных условиях у(t), x(t), u(t).
Уравнение устройства для замера угловых скоростей выходного вала двигателя внутреннего сгорания
m |
d 2l |
k |
dl |
k |
l 3 |
k |
(2) |
dt 2 |
|
||||||
|
dt |
c |
|
|
|
||
Описывает всѐ устройство на неопределѐнном промежутке времени. m – масса устройства;
l – перемещение этой массы;
kν – коэффициент скоростного трения; kc – коэффициент жѐсткости пружины;
ω – угловая скорость (частота вращения).
Введѐм: l l1 l1 l2 ,
5
тогда получим:
l1 |
l2 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
l2 |
|
k |
l1 |
|
kc |
|
|
k |
|
(3) |
|
|
|
l13 |
|
|
|||||||
m |
m |
m |
|
||||||||
|
|
|
|
|
|
|
|
||||
описывает состояние устройства.
Можно рассчитывать состояние устройства в любой заданной промежуток времени.
Уравнение ракеты, вертикально стартующей под действием силы тяги
|
|
|
|
d 2 H |
|
|
|
dh 2 |
|
|
|
dm t |
|||||||||
(4) m t |
|
|
|
|
k |
|
|
|
|
|
m t g k |
|
|
||||||||
dt 2 |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
dt |
|
|
|
|
|
|
dt |
||||||||
h h1 , |
h1 h2 |
|
|
|
|
|
|
|
|
|
|
Уравнение ракеты: |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
dm |
|
|
1 |
|
|
|
k h12 |
g . |
|
|
|
||||||||
h2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
d |
m t |
|
m t |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Разностное уравнение для описания элементов дискретного действия |
||||||||||||||||||||
y tk 1 |
f |
y tk |
,u tk |
|
,tk |
|
|
|
|
||||||||||||
x tk g y tk ,u tk ,tk |
|
|
(1) |
||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
|
y |
|
|
|
|
|
|
u |
|
|
|
x |
|
||||||
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|||||
y tk |
y2 |
|
|
|
|
|
u2 |
|
|
x2 |
|||||||||||
. |
|
u tk |
|
. |
|
|
x tk |
. |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
. |
|
|
|
|
|
|
|
. |
|
|
|
. |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
yn |
|
|
|
|
|
|
un |
|
|
xn |
|
|||||||
|
f |
|
|
|
|
g |
|
|
|
1 |
|
|
|
1 |
|
f y tk , u tk , tk |
f2 |
g y tk , u tk |
, tk |
g2 |
|||
. |
|
. |
|
||||
|
|
|
|
|
|
|
|
|
. |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
fn |
|
|
|
gn |
|
|
Описывает состояние дискретного элемента. Здесь не учитывается такт квантования, поэтому для решения эти уравнения очень сложные.
Такт квантования системы – это та частота, с которой опрашиваются датчики. Теперь эта же система с тактом квантования:
y k 1 T |
f y kT |
,u kT |
, kT |
|
|
|
0 |
0 |
0 |
|
0 |
|
(2) |
x kT0 g y kT0 ,u kT0 , kT0 |
|
|
|
|||
Для написания программы системы управления используют три метода:
6

Эйлера.
U k 1 U1k T0Uk .
Адамс-Балифорт.
U1 k 1 U1 k 1 2T0Uk .
Адамс-Мультон.
U1 k 1 U1 k 1 T30 Uk 4Uk 1 Uk 2 .
U – сигнал (выходной, входной или сравниваемый); To – такт квантования;
Tk-1,k-2 – предыдущие сигналы; Tk – настоящий сигнал;
Tk+1 – следующий сигнал.
Вопросы самоконтроля:
1.Как описываются переменные состояния ЛСУ?
2.Как описываются переменные состояния дискретных объектов ЛСУ?
3.Метод Эйлера.
4.Метод Адамса-Башфорта.
5.Метод Адамса-мультона.
ЛЕКЦИЯ №3 Цель лекции: Изучить математические методы линеаризации нелинейных уравнений объектов управления.
Задачи лекции:
1.Четыре метода линеаризации нелинейных уравнений объектов управления.
2.Описание стационарных объектов управления ЛСУ.
Желаемый результат:
Студенты должны знать:
1.Перечислите методы линеаризации нелинейных уравнений объектов управления;
2.Как линеаризуются графики нелинейных функций в рабочей области;
3.Как проводится линеаризация методом наименьших квадратов.
Учебный материал Методы линеаризации уравнений
Четыре метода линеаризации.
1.Нелинейная функция в рабочей области раскладывается в ряд Тейлора.
2.Заданные в виде графиков нелинейные функции линеаризуются в рабочей области прямыми.
3.Вместо непосредственного определения частных производных вводятся переменные в исходные уравнения.
7
y y0 |
y |
|
x x0 |
|
|
x |
(3) |
|
u u0 |
|
|
u |
|
4. Проводит линеаризации нелинейных характеристик по методу наименьших квадратов или методом трапеции.
W1
W3
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W2 |
|
W4 |
|
|
|
|
||
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
W3 |
|
|
|
|
|
|
W1 |
|
W2 |
|
|
|
|
|
|
|
|
W4 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
W3 |
|
|
|
|||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
Сначала составить структурную схему и объединить передаточные функции.
Написать, как это упростить до W1234.
При проектировании непрерывных, дискретно-непрерывных и дискретных систем необходимо знать математические модели объектов управления.
Система дискретных уравнений, передаточные функции, частотные характеристики и импульсные переходные функции удобны лишь при невысоких порядках математических моделей.
При высоких порядках моделей используют векторно-матричный аппарат запи-
си уравнений. |
|
||||
Стационарный объект описывается уравнением: |
(4) |
||||
|
y t Ay t Bu t |
||||
|
|
|
|
|
|
|
Ay t y t Bu t |
(5) |
|||
|
A |
y t |
1 |
y t u t |
(6) |
|
|
|
|||
|
B |
B |
|
||
В соответствии с этим уравнением существует типовая структурная схема многомерного объекта.
|
|
Bu(t) |
|
|
|
|
у(0) |
||
u(t) |
|
y |
(t) |
|
|
|
|
||
В |
|
1/Р |
|
|
у(t) |
||||
|
|
|
|
|
|
|
|||
|
|
Ау(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 – потому что много состояний.
– потому что много состояний.
Нестационарный объект:
8
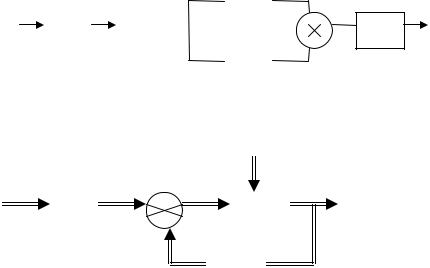
y t A t y t B t u t
(схему нарисовать см)
Решение:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W3 |
|
|
|
|
|
|
W1 |
|
|
|
|
|
W2 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. A t y t |
y t |
B t u t |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
A t |
|
y t |
1 |
|
y |
t u t |
|||||||||||
|
|
B t |
||||||||||||||||
|
B t |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
B(t)u(t) y(t) |
у(0) |
||||||
u(t) |
|
|
|
|
|
|
|
|
|
|
||||||||
В(t) |
|
|
|
|
|
|
1/Р |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
А(t)у(t) |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
А(t) |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W4
у(t)
Вопросы самоконтроля:
1.Рассмотрите линеаризацию нелинейных функций методом наименьших квадратов?
2.Рассмотрите линеаризацию графиков нелинейных функций в рабочей области?
3.Рассмотрите линеаризацию нелинейных функций разложением в ряд Тейлора.
ЛЕКЦИЯ №4 Цель лекции: Изучить математические модели нелинейных объектов ЛСУ,
линеаризация нелинейных элементов ЛСУ с помощью коэффициентов линеаризации.
Задачи лекции:
1.Математические модели нелинейных объектов ЛСУ.
2.Коэффициенты линеаризации.
Желаемый результат:
Студенты должны знать:
1.Существующие виды нелинейных объектов управления ЛСУ;
2.Математическое описание коэффициентов линеаризации нелинейных объектов ЛСУ.
Учебный материал Математические модели нелинейных объектов.
Весь класс существенных нелинейностей делится на 2-ве группы. К первой группе относятся однозначные нелинейности, у которых связь между входным
9
и выходным
y
-а 0
векторными сигналами зависит только от формы статической ха-
|
|
рактеристики. |
|
|
|
y=F(x) |
|
|
|
x(t)=x1(t) |
|
в |
|
y1(t)=a(x1)x1(t) |
(1) |
|
|
||
|
а |
|
|
|
|
x |
|
-в |
|
|
|
Из (1) получаем приближѐнное значение передаточной функции: |
|
y x1 a x1 |
(2) |
Ко второй группе относятся двузначные нелинейности, у которых связь между входным и выходным сигналами зависит не только от формы статической характеристики, но и от предыстории входного сигнала.
y
в
-а |
0 |
а |
x
-в
Для учѐта предыстории влияния входного входной сигнал, но и скорость его изменения. y(t)=F[x(t)]
x(t)=x1(t)
y1 t a x1 x1 b x1 T x1
2
сигнала, учитывается не только
(3)
(4)
a(x1), b(x1) – коэффициенты гармонической минерализации двузначных нелинейностей; Т – период колебаний в 1-й гармонике.
Эквивалентная передаточная функция: |
|
|||||||
y(x1)=a(x1)+jb(x1) |
|
|
|
(5) |
||||
То есть, в общем, виде можно записать: |
|
|||||||
|
~ |
, x1 |
|
|
|
|
|
|
y t F x1 |
~ |
|
|
|
|
|||
|
|
|
|
|
|
|
||
|
~ |
|
|
b x1 , x1 |
|
|
||
y t |
a x1 , x1 |
|
|
|
x1 |
(6) |
||
2 k |
|
|
||||||
|
|
|
|
|
|
|
|
|
k – номер гармоники. |
|
|
|
|
||||
~ |
~ |
|
|
~ |
|
(7) |
||
|
|
|||||||
y x1 |
a x1, x1 |
jb x1, x1 |
||||||
10
