
Лекции / леккции
.pdf
При последовательном программировании передаточную функцию преобразуют к виду:
|
|
|
|
|
W1 z |
W2 z |
|
Wn z |
||||||
|
|
z |
|
|
|
|
||||||||
W z |
U |
1 |
|
|
1 e z 1 |
|
1 e z n |
|||||||
1 |
|
|
|
|
|
|
1 |
|
|
... |
|
n |
|
|
U z |
|
1 d |
z 1 |
1 d |
z 1 |
1 d |
m |
z m |
||||||
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
||
1/en и 1/dm – соответственно нули и полюса характеристического уравнения. |
|||||||||||||||
W z W1 z W2 |
z ... Wn z |
|
|
|
|
|
|
||||||||
При параллельном программировании: |
|||||||||||||||
|
W1 z |
|
|
W2 z |
|
W3 z |
|
Wn z |
|||||||
|
|
|
|
|
|
|
|
||||||||
W z |
P |
|
|
P |
|
|
|
P |
|
... |
P |
|
|
||
1 |
|
|
2 |
|
|
3 |
|
|
n |
|
|
||||
1 d z 1 |
1 d |
z 1 |
1 d |
z 1 |
1 d |
m |
z 1 |
||||||||
|
1 |
|
|
2 |
|
|
|
3 |
|
|
|
|
|
||
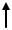 U1(z)
U1(z)
W1(z) |
|
W2(z) |
|
W3(z) |
|
Wn(z) |
|
|
|
|
|
|
|
U(z)
Если есть Wky(jλ)=, то можем составить программу коррекции. 1) Производим обратно билинейное преобразование:
Wky |
j Wky |
z |
|
|
0,05z2 0,04z 1 |
|||||
0,06z3 |
0,03z2 0,01z 1 |
|||||||||
|
|
|
|
|
|
|||||
2) Делаем сдвиг на (z-1) |
||||||||||
|
|
~ |
|
|
|
|
|
|
||
W |
z |
U z |
|
, |
|
|
|
|
||
U z |
|
|
|
|
||||||
|
ky |
|
|
|
|
|
|
|||
т.е. домножаем на (z-1). |
|
|||||||||
|
|
|
|
|
~ |
|||||
|
|
0,05z 0,04 z 1 U |
z |
|||||||
0,06z 2 0,03z 0,01 z 1 U z |
|
|||||||||
Запишем разностное уравнение в масштабе реального времени, вместо z2→Uk-2, z→Uk-1.
Сначала запишем знаменатель с противоположным знаком, затем числитель |
|||||
~ |
z 0,06Uk 2 |
0,03Uk 1 0,01Uk |
~ |
~ |
~ |
Uky |
Uk 1 0,05Uk 1 |
0,04Uk |
Uk 1 |
||
Это уравнение и программируется.
Вопросы самоконтроля:
1.Перечислите порядок реализации корректирующих устройств в дискретных локальных системах управления.
2.Назовите виды программирования корректирующих устройств локальных систем управления.
31
ЛЕКЦИЯ №13 Цель лекции: Изучить порядок расчета передаточной функции двигателя.
Задачи лекции:
1. Порядок расчета передаточной функции двигателя.
Желаемый результат:
Студенты должны знать:
1. Порядок расчета передаточной функции двигателя.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Учебный материал |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Расчѐт ПФ двигателя. |
|
|||||
W S |
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
S T |
2 S 2 2T 2 S 1 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Элек- |
|
k |
|
|
|
|
|
|
kM |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
km – моментальная постоянная |
|||||
триче- |
|
Ra k |
km ke |
|
|
|
|
|
|
|
|
|
|
|
|
электродвигателя |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
ский |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ra – сумма сопротивлений об- |
|
|
|
|
|
|
|
|
|
|
|
J |
|
|
R T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
T |
|
|
|
|
|
A |
|
a g |
|
|
|
|
|
|
|
|
|
|
|
|
моток якоря электродвигателя, |
|||||||
|
|
Ra k |
km ke |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
соединительных проводов и |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
Ra J n Ra k Tg |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
выходной цепи электромаг- |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
2 J n RaTg Ra k km ke |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
нитного усилителя |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kν – коэффициент вязкого тре- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ния |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ke – постоянная противо-эдс |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Jn – приведѐнный к валу дви- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
гателя момент инерции вра- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
щающихся частей и исполни- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тельного механизма |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Tg=La/Ra – электромагнитная |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
постоянная якоря |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ra – омическое сопротивление |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
La – индуктивное сопротивле- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ние |
Гид- |
|
k |
|
|
|
kn kгд |
|
|
|
|
|
|
|
|
|
|
|
kn – постоянная гидравличе- |
||||||||||||
равли- |
|
k 2 |
|
|
k |
|
k |
y |
|
|
|
ской помпы |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
гд |
|
|
|
|
|
|
|
|
|
||||||||||
ческий |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kгд – постоянная гидродвигате- |
|
T |
|
|
|
|
|
|
|
VJ n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ля |
||||||||
|
|
|
E k |
2 |
k k |
y |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
гд |
|
|
|
|
|
|
|
|
|
|
|
|
kω – коэффициент жидкостно- |
||||
|
|
|
|
|
|
|
|
|
|
|
Jn ky E Vk |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
го трения |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
VE Jn kгд2 |
|
k ky |
|
|
|
ky – коэффициент, характери- |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
зующий утечки гидравличе- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ского привода |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V –объѐм рабочей жидкости в |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
цилиндре при нормальном |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
давлении |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E – модуль объѐмной упруго- |
32

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сти |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Jn – приводимый к валу двига- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
теля момент инерции всех |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вращающихся частей |
Пнев- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P10 – установившееся давление |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
n |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
матиче- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
P |
|
|
n |
|
P |
|
n |
|
|
|
в 1-ой и 2-ой полостях силово- |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
P n |
|
|
|
P |
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
20 |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
20 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
ский |
|
|
|
|
|
|
P |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P20 |
|
|
|
Pa |
|
|
|
|
|
го цилиндра |
||||||||||||||
|
|
|
|
|
|
10 |
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
двига- |
k |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P0 – давление воздуха в резер- |
||||||||||
|
|
nP0 |
|
|
|
|
nP20 |
|
|
|
|
|
|
|
|
nP0 |
|
|
|
|
nP20 |
|
|
|
|
|
||||||||||||||||||||||
тель |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вуаре |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
X n0 |
|
|
L X n0 |
|
|
|
|
|
|
|
X n0 |
|
L X n0 |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pa – атмосферное давление |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
окружающей среды |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mXn0 L X n0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Xn0 – величина перемещения |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
F nP L X nP X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
поршня |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
n |
10 |
|
|
|
n0 |
20 |
|
|
n0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
nP L X |
|
|
P X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L – длина силового цилиндра |
||||||||||||||
|
|
|
|
|
|
|
10 |
|
|
|
|
n0 |
20 |
|
n0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
Fn mXn0 L X n0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
за вычетом толщины поршня |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n – показатель политропы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
λ1, λ2 – постоянные привода |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fn – площадь поршня |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m – масса поршня, штока и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
подвижных частей исполни- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тельного механизма |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kν – постоянная скоростного |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
трения |
Передаточное соотношение редуктора: |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
J n |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
J g |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Jn – момент инерции на валу двигателя, Jg – момент инерции объекта управления.
Привод будет согласован с нагрузкой при следующих номинальных параметрах.
|
|
|
|
|
|
|
||
M n 2E J n J g |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Jn |
|
|||||
n m |
|
|
||||||
|
|
|
|
|
рассчитать после подбора двигателя и редуктора |
|||
J g |
||||||||
|
|
|
||||||
|
|
|
||||||
|
|
|
|
|
|
|
|
|
Wn 2 m Em J n |
|
|||||||
|
|
|
|
|
|
|
|
|
Wn – мощность
Em и ωm – максимальная угловая скорость и максимальное ускорение углового вала.
Вопросы самоконтроля:
1.Порядок расчета передаточной функции двигателя.
2.Порядок расчета передаточной функции привода.
33
ЛЕКЦИЯ №14 Цель лекции: Изучить порядок сравнения подобранных вычислительных устройств.
Задачи лекции:
1.Порядок сравнения подобранных вычислительных устройств.
2.Критерии оценки.
Желаемый результат:
Студенты должны знать:
1. Порядок сравнения подобранных вычислительных устройств.
Учебный материал Критерии выбора вычислительных устройств
После подбора управляющих вычислительных устройств рассчитываются три критерия:
1) критерий технической эффективности.
В качестве этого критерия используется эффективное быстродействие машины.
Jt max Vэфj k jVномj
– номинальное быстродействие, определяемое быстродействием элемемнтов машины.
kj – коэффициент пропорциональности:
kj=kэфj·kkj·kнпj
kэфj – коэффициент учитывающий эффективность системы команд машины, особенности структуры машины,
kkj – коэффициент учитывающий снижение быстродействия за счѐт включения в систему средств, обеспечивающих требуемую надѐжность,
kнпj – коэффициент учитывающий потери времени на профилактику и устранение неисправностей.
kj должно быть <1,
j – номера сравниваемых машин.
2) Критерий технико-экономической эффективности.
В основу этого критерия положен показатель, называемый критерием цены эффективности БД.
Сущность этого критерия заключается в определении показателя, который бы давал оценку стоимости выполнения одной операции.
|
|
|
L2 j t |
|
|
J mэ |
min gi |
|
|
|
|
tVэфj |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
показатель должен быть минимальным, gi – цена эффективности БД,
L2j(t) – общая сумма затрат на постройку и эксплуатацию машины в течение времени t до момента его полного износа.
3) Критерий экономической эффективности (критерий минимальных затрат)
34
J min Wпр С j нормWэj
Wпр – приведѐнные затраты,
Сj – единовременные капитальные затраты, имеющие место в момент установки, τнорм – нормальный срок окупаемости,
Wэj – эксплуатационные расходы в 1-й момент времени.
Вопросы самоконтроля:
1.Порядок сравнения подобранных вычислительных устройств.
2.Критерии оценки.
ЛЕКЦИЯ №15
Цель лекции: Изучить виды адаптивных систем, системы адаптивного регулирования.
Задачи лекции:
1.Системы экстремального регулирования.
2.Способ синхронного детектирования.
Желаемый результат:
Студенты должны знать:
1.Определение системы экстремального регулирования.
2.Математическое описание системы экстремального регулирования.
3.Использование способа синхронного детектирования.
Учебный материал Адаптивные системы
1. Системы экстремального регулирования
Системами экстремального регулирования называются системы, в которых задающие воздействия, то есть заданные значения регулируемых величин, определяются автоматически, в соответствии с экстремумом некоторой функции F(y1, y2, …yn). Эта функция зависит не только от регулируемых величин y1, y2, …yn, но и от неконтролируемых параметров системы и времени. Поэтому она не является постоянной и заранее известной. Однако, изменение функции F и величин y1=y1э, y2=y2э, …yn=ynэ протекает относительно медленно.
Условием экстремума дифференциальной функции нескольких переменных является равенство нулю в точке экстремума частных производных этой функции.
F |
0 ; |
F |
0 ; |
F |
0 ; …; |
F |
0 |
(1) |
||
y |
y |
2 |
y |
y |
n |
|||||
1 |
|
|
|
3 |
|
|
|
|
||
Градиентом функции называется векторная величина:
|
|
|
dF |
|
|
|
dF |
|
|
|
dF |
|
|
|
dF |
|
||||
gradF k1 |
k |
2 |
k3 |
... k |
n |
(2) |
||||||||||||||
dy |
dy |
2 |
dy |
3 |
dy |
n |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
где k1, k2, k3, …,kn – единичные векторы осей, по которым отсчитываются вели-
чины y1, y2, y3, …,yn.
В точке экстремума gradF=0 (3) Задача поиска экстремума разбивается на 2-ве:
35

1. определение градиента,
2. организация движения в точке экстремума.
Способ синхронного детектирования
Основан на том, что к основным медленно меняющимся величинам добавляются малые гармонические составляющие:
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
y1 |
y1 |
A1 sin 1t |
|
|
|
|
|
|
|
|
|
||
y |
2 |
y0 |
A sin |
2 |
t |
|
|
|
|
|
|||
|
2 |
2 |
|
|
|
|
|
|
|
|
|
||
............................. |
|
|
|
|
(4) |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yn0 |
An sin nt |
|
|
|
|
|
|||||
yn |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
sinω1t |
|
|||||
|
|
|
A1sinω1t |
|
|
|
CD1 |
sinω2t |
U1 |
||||
|
|
|
|
Регулируемый |
|||||||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
A2sinω2t |
|
|
|
|
|
|
sinω3t |
U3 |
||
|
|
|
|
|
|
|
CD2 |
||||||
|
|
|
A3sinω3t |
|
объект |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
U3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
CD3 |
|
|
|
|
|
|
|
|
|
|
|
|||||
Величина F поступает на асинхронные детекторы, у которых в качестве переменных величин используются те же временные составляющие.
Идеальные синхронные детекторы умножают величину F на переключающую
функцию, представляющую собой прямоугольную волну с периодом Ti 2 ,
i
i=1, 2, 3, …,n и высотой =1.
Переключающая функция приблизительно может быть заменена синусоидальной частотой ωi с амплитудой, поэтому среднее значение выходных величин синхронных детекторов могут быть представлены следующим образом:
U |
|
|
|
|
|
|
|
|
F sin t |
|
|||||
|
1 |
|
1 |
|
|
|
|
U |
2 |
F sin 2t |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F sin 3t |
(5) |
|||||
U 3 |
|||||||
..................... |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F sin nt |
|
|||||
U n |
|
||||||
|
|
|
|
|
|
|
|
В квазистационарном режиме, когда составляющие y10 медленно меняются поисковым движением sinω1t, величины U1, U2, U3, …Un с точностью до малых порядков пропорциональны соответствующим частным производным и, следовательно, определяют градиент в этой точке.
Разложим функцию F в окрестности этой точки в степенной ряд.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
0 |
|
|
F y10 y1 , y20 |
y2 ... yn0 yn F y10 , y20 ,...yn0 |
dF |
|
yi |
|||||||||||||||||||
dyi |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i 1 |
(6) |
|||
|
1 |
|
n |
d |
2 |
F |
0 |
|
|
1 |
|
n |
d |
3 |
F |
0 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
yi yk |
|
|
|
|
|
yi yk y |
|
|
|
||||||||
2! |
dy |
dy |
|
3! |
dy |
dy |
|
|
|
|
|||||||||||||
|
i,k 1 |
k |
|
|
i,k , 1 |
dy |
|
|
|
||||||||||||||
|
|
|
|
i |
|
|
|
|
|
|
i |
|
|
k |
|
|
|
|
|||||
36

y1=A1sinω1t yn=Ansinωnt
Величину СD можно представить:
|
|
|
|
|
|
|
n |
|
0 |
|
||
U g |
F sin g t F y10 , y20 ,...yn0 sin g t A1 |
dF |
|
sin it sin g t |
||||||||
dyi |
||||||||||||
|
|
|
|
|
|
|
i 0 |
(7) |
||||
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
|
n |
dF |
0 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|||||
|
|
Ai Ak |
|
sin it sin k t sin g t ... |
|
|
|
|||||
|
|
dyi dyk |
|
|
|
|||||||
|
2! i,k 0 |
|
|
|
|
|
|
|||||
Если величины y1, y2, y3, …yn постоянны или медленно меняются так, что их изменениями за небольшой период можно пренебречь, тогда все значения sin можно приравнять к 0.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
g |
t 0 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin g t |
0 |
|
|
|
|||||||
sin it |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
|
t |
sin |
|
t sin |
t 0 |
|
||||||||
|
i |
|
|
|
|
|
k |
|
|
g |
|
|
|
||
U g |
1 |
|
Ag |
dF 0 |
U g |
(9) |
|||||||||
|
|
dyg |
|||||||||||||
|
|
|
2 |
|
|
|
|
|
|
||||||
где Ug – погрешность.
Величина погрешности по отношению к амплитудам А1, А2, …Аn имеет порядок не ниже 3-го, а по сравнению с величиной выходного сигнала – не ниже 20-го. Выходная величина синхронного детектирования с достаточной степенью точности можно считать пропорциональной составляющим градиента y10, y20, …yn0.
Вопросы самоконтроля:
1.Дайте определение системы экстремального регулирования.
2.Математическое описание системы экстремального регулирования.
3.Использование способа синхронного детектирования.
ЛЕКЦИЯ №16
Цель лекции: Изучить способы поиска градиента адаптивных систем.
Задачи лекции:
1.Способ производной по времени.
2.Способ запоминания экстремума.
3.Способ Гаусса-Зайделя.
4.Способ градиента.
5.Способ наискорейшего спуска.
Желаемый результат:
Студенты должны знать:
1.Способ производной по времени.
2.Способ запоминания экстремума.
3.Способ Гаусса-Зайделя.
4.Способ градиента.
5.Способ наискорейшего спуска.
37

Учебный материал Способ производной по времени
Производная по функции времени определяется выражением:
dF |
|
dF |
|
dy1 |
... |
dF |
|
dyn |
(1) |
|
dt |
dy1 dt |
dyn dt |
||||||||
|
|
|
||||||||
Из выражения (1) следует, что, задавая поочерѐдно скорости изменения y1, y2,
…yn и производную по времени dFdt , можно найти составляющие градиенты.
Недостатком этого метода является необходимость дифференцирования функции F по времени, что сопровождается поднятием уровня высокочастотных помех.
Способ запоминания экстремума
Этот способ заключается в том, что система совершает вынужденное или автоколебательное движение в зоне экстремума.
При достижении экстремального значения F=Fэ, оно фиксируется на запоминающем устройстве. Градиент функции определяется по разности текущего и экстремального значения.
Способ Гаусса-Зайделя
Способ заключается в поочерѐдном изменении координат y1, y2, …yn. Сначала фиксируются координаты с y2 до yn, а координата y1 изменяется так, чтобы соответствующая градиента стала =0:
y1 dF 0 dy1
Затем фиксируются все координаты от y3 до yn :
y2 dF 0 dy2
и так далее
до yn dF 0 dyn
После этого возвращаются к началу и повторяют весь цикл снова.
Этот процесс продолжается до тех пор, пока не будет получена точка экстремума.
Способ градиента
Вэтом способе осуществляется одновременное изменение всех координат так, чтобы обеспечить движение системы в направлении близком к мгновенному направлению вектора градиента.
Впростейшем случае непрерывного безынерционного управления должны быть реализованы следующие зависимости:
38
y |
k |
dF |
|
|
|
|
|
dy |
|
|
|
|
|||
1 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
y2 |
k |
|
dF |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
||||
|
|
|
dy2 |
(2) |
|||
|
|
|
|
|
|
|
|
............... |
|
|
|
||||
|
|
|
|
|
|
|
|
yn |
k |
|
dF |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|||
|
|
|
dyn |
|
|||
Здесь k – коэффициент пропорциональности.
Для получения правильного направления движения для случая экстремума максимума – k>0, экстремума минимума – k<0.
Уравнение (2) соответствует устойчивому движению экстремальной системы, при котором производная от F сохраняет свой знак всюду, кроме точки экстремума.
При шаговом движении:
|
k |
|
dF |
|
|
|
|
|
|
|
|
||
y1 |
dy1 |
|
||||
|
|
|
|
|||
|
|
|
dF |
|
|
|
|
k |
|
|
|
||
|
|
|
||||
y2 |
|
dy2 |
|
|
||
|
|
|
|
|
||
|
|
|
|
|
|
|
.................... |
||||||
|
|
|
|
|
|
|
|
|
|
dF |
|
|
|
|
k |
|
|
|
||
|
|
|
|
|||
yn |
|
dyn |
|
|
||
|
|
|
|
|
||
y1 , y2 , … yn
(3)
– фиксированные шаги в направлении экстремумам.
Способ наискорейшего спуска
При способе наискорейшего спуска движение происходит по начальному направлению вектора градиента до тех пор, пока производная функция F по этому направлению не обратится в нуль. Затем опять определяется направление градиента и происходит движение вдоль этого вектора до обращения в нуль производной от F по этому направлению. Процесс повторяется до достижения точки экстремума.
Рассмотрим схему экстремального регулирования настройки колебательного контура.
39

R
C1 C2
L Um
|
|
ω1 |
|
|
|
|
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Φ1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Д2 |
|
|
|
|
|
|
CD |
|
|
|
|
ГОН |
|
||||||
|
|
|
|
|
|
|||||
|
|
|
||||||||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|||||
|
|
|
|
|||||||
Д1 |
Φ1 |
|
|
|
|
|
||||
|
|
|
|
|
||||||
Общая ѐмкость колебательного контура: |
||||||||||
с=с1+с2+с20+Аsinω1t |
(4) |
|||||||||
Здесь с20 – постоянная составляющая ѐмкости конденсатора с2, ω1 – угловая частота вращения ротора.
ω1 выбирается так, чтобы она была во много раз меньше частоты полезного сигнала ω=2πf и больше возможной частоты процесса регулирования.
Двигатель Д2 |
синхронно с вращением конденсатора ротора с2 даѐт опорную ве- |
личину и |
в виде опорного напряжения той же частоты от генератора |
ГОН. |
|
Переменное напряжение на колебательном контуре после выпрямления и сглаживания фильтром F1 поступает на вход синхронного детектора. На выходе синхронного детектора формируется сигнал, пропорциональный производной
от амплитуды напряжения контура по ѐмкости dUdCm .
Этот сигнал после сглаживания фильтром F2 поступает далее на усилитель и двигатель Д1. последний будет изменять регулируемую величину и произво-
дить подстройку до тех пор, пока производная dU m не станет =0. dC
Всякое изменение частоты сигнала будет вызывать автоматическую подстройку на максимум напряжения на контуре.
В рассматриваемой экстремальной системе получается своеобразная следящая система, ошибкой которой является производная dUdCm , поэтому эта схема мо-
жет быть приведена к соответствующей структурной схеме:
40
