Совместная гармоническая и статическая линеаризация
При поступлении на вход нелинейного элемента сумма двух сигналов периодического случайного:
.
(119)
Коэффициенты линеаризации являются периодическими функциями времени, то есть
.
(120)
Применить выражение (120) совместную гармоническую и статическую линеаризацию, получит приблизительную зависимость:
,
(121)
,
(122)
,
(123)
.
(124)
Выражение (110),
(114), (115) представляет собой усредненные
за период
значение гармонической составляющей
передаточной функции и статических
коэффициентов.
Дискретных нелинейных элементов
Квантование по времени в ЛСА осуществляется импульсными устройствами на основе трех типов модуляции: АИМ, ШИМ, ЧИМ. Быстродействующие устройства с АИМ являются линейными импульсными элементами, а устройства с ШИМ и ЧИМ – нелинейными.
Нелинейный импульсный элемент для удобства математического описания можно представить в виде совокупности линейного и нелинейного элемента. Сигнал на выходе с двухзначного нелинейного элемента записывается в виде:
,
(126)
где
.
(127)
При этом будем считать, что входной сигнал является гармоническим, то есть
,
(128)
где
;
(129)
- полупериод
гармонического колебания, (
).
.
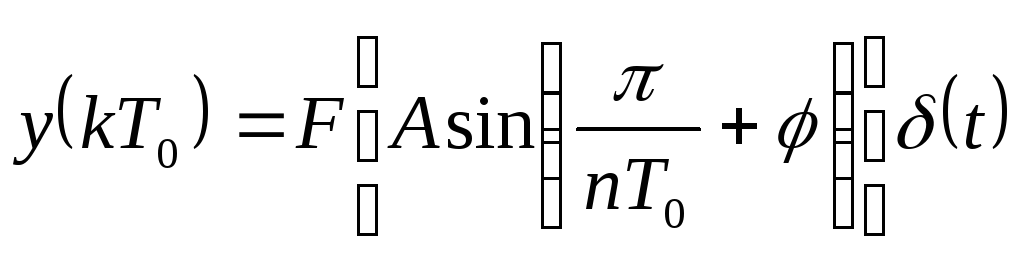(130)
При учете первой гармоники, выходной сигнал будет равен:
,
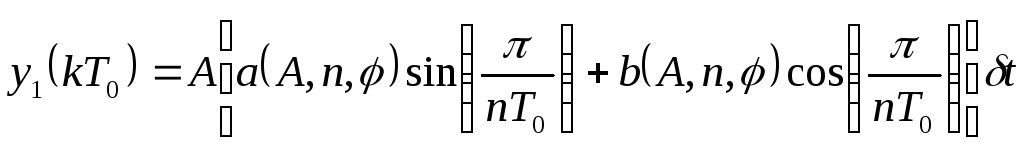(131)
Определим условие
наилучшего квадратичного приближения
к
для этого запишем соотношение:
,
(132)
где
- полупериод функции
.
.
(133)
После преобразования получим
,
(134)
.
(135)
Пользуясь этими двумя формулами, найдем эквивалентную передаточную функцию.
,
(136)
где
,
(137)
.
(138)