Общий метод описания эквивалентных передаточных функций нэ

Весь класс существенных нелинейностей разделены на две группы. К первой группе относится однозначные нелинейности, у которых связь между входными и выходнымивекторными сигналами зависит только от формы статической характеристики нелинейности.

. (41)

Рисунок 15

В этом случае, при определенной форме входных сигналов:

. (42)

С помощью матрицы линеаризации можно найти приближенное значение выходных сигналов:

. (43)

Из (42) следует, что матрица коэффициентов линеаризации однозначных нелинейностей, является действительными величинами и их эквивалентные передаточные функции:

. (44)

Ко второй группе относят двузначные (многозначные) нелинейности, у которых связь между входными и выходными сигналами зависит не только от формы статической характеристики, но так же определяется предысторией входного сигнала. В этом случае выражение (42) запишется в виде:

. (45)

Рисунок 16 – Двузначная нелинейность

Для учета влияния предыстории входного периодического сигнала будем учитывать не только сам сигнал , но и скорость его изменения, дифференциал.

При входных сигналах:

приближенное значение входного сигнала будет:

, (46)

где и- коэффициенты гармонической линеаризации двухзначных нелинейностей;

- период колебания по правой гармонике;

- гармоническая функция.

Эквивалентная передаточная функция:

. (47)

Существуют нелинейности более общего вида:

, (48)

, (49)

где и- коэффициенты гармонической линеаризации;

- номер гармоники.

Матрицы коэффициентов линеаризации периодической с периодом . Имея это ввиду, передаточную функцию двух двухзначной нелинейности (48) можно представить по аналогии с передаточной функцией (47).

. (50)

Пользуясь (44), (46) и (49) определим обобщенную формулу для вычисления передаточной функции однозначных и двухзначных нелинейностей.

В случае однозначной нелинейности матрица коэффициентов линеаризации , зависящей от параметров вектора, выберем, таким образом, чтобы линеаризовать среднее значение квадрата разности между точными приближеннымсигналами на входе:

, (51)

где «черта сверху» - это силовое усреднение.

. (52)

После преобразований, упрощений, ухищрений и усиления бдительности, получим эквивалентную передаточную функцию в виде системы матриц: ,.

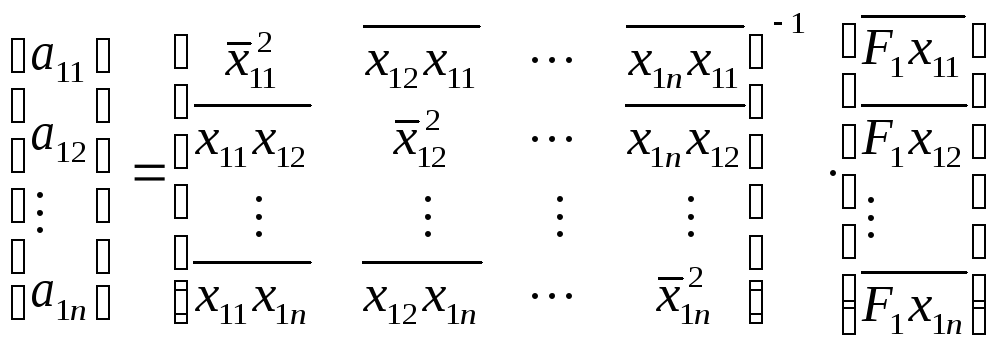, (53)

при ,.

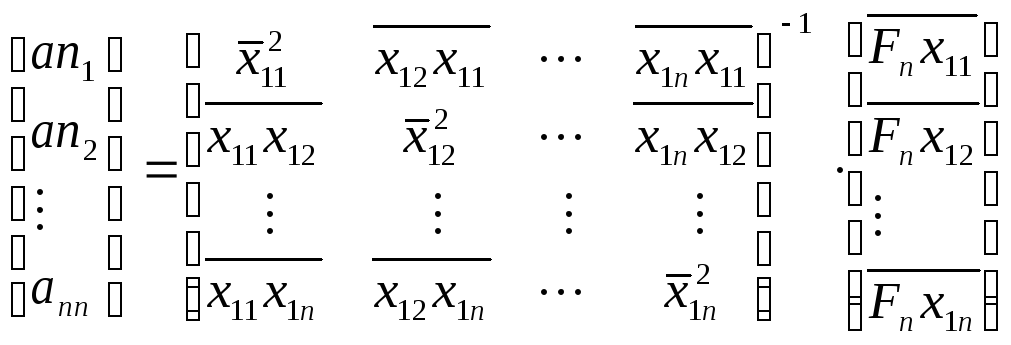. (54)

Пример.

Определить коэффициент линеаризации для однозначной нелинейности. Когда на ее вход поступает первая гармоника синусоидального сигнала:

, (55)

где .

. (56)

Уравнение (56) представляет собой коэффициент линеаризации по первой гармонике для однозначной нелинейности, она определяет эквивалентную передаточную функцию .

В дальнейшем сравнение формулы для определения коэффициентов линеаризации простейших нелинейностей при подаче на их вход периодических сигналов: синусоидального, треугольного, покажем целесообразность применения получаемых эквивалентных передаточных функций.

Перейдем к распределению обобщенного метода описания коэффициентов линеаризации на двухзначные нелинейности.

В этом случае, учитывая соотношение (50) и (52), можно записать:

, (57)

Уравнение (52) примет вид

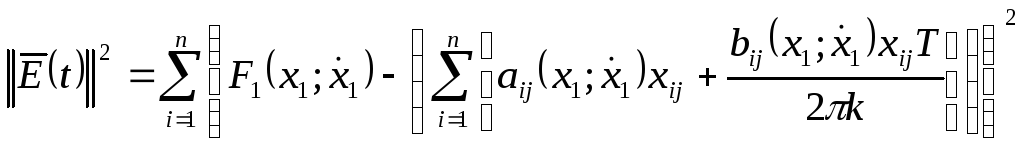. (58)

Коэффициент линеаризации определим (58) ,.

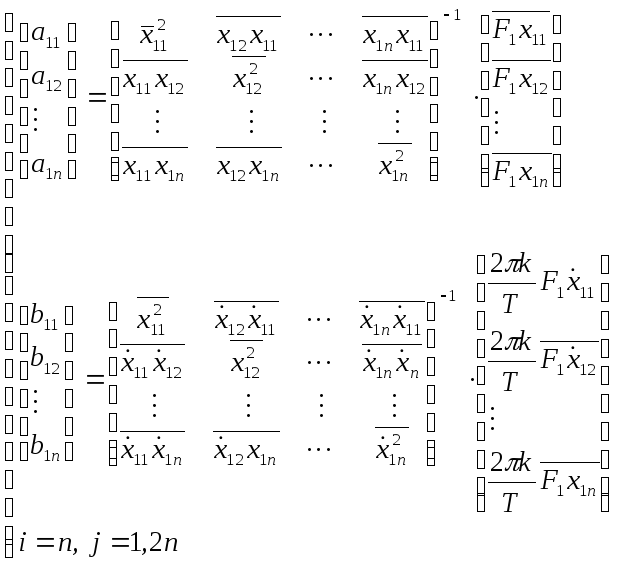, (59)

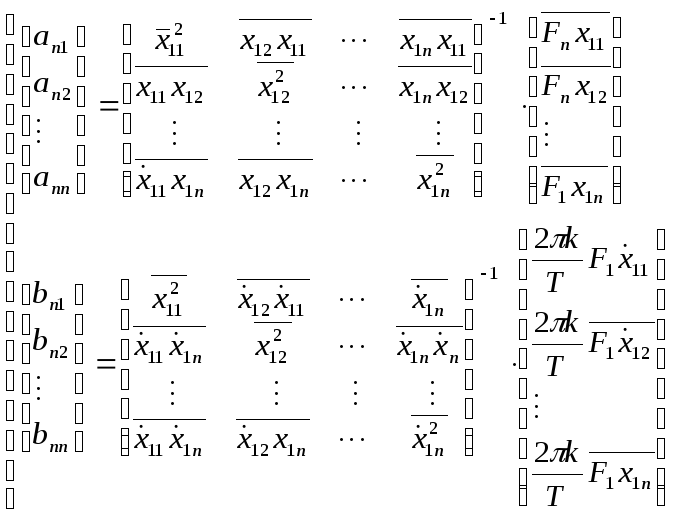. (60)

Пример. Определить коэффициент линеаризации двузначной нелинейности, когда на ее вход поступает первая гармоника синусоидального сигнала и имеет один вход. Из системы матриц (60), получим:

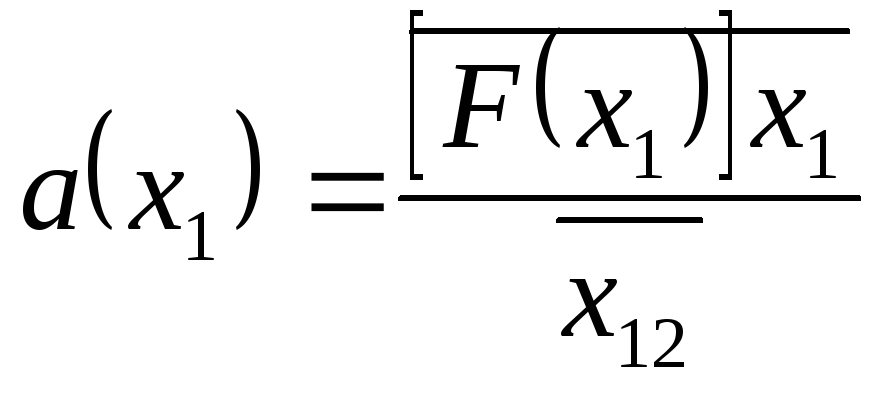, (61)

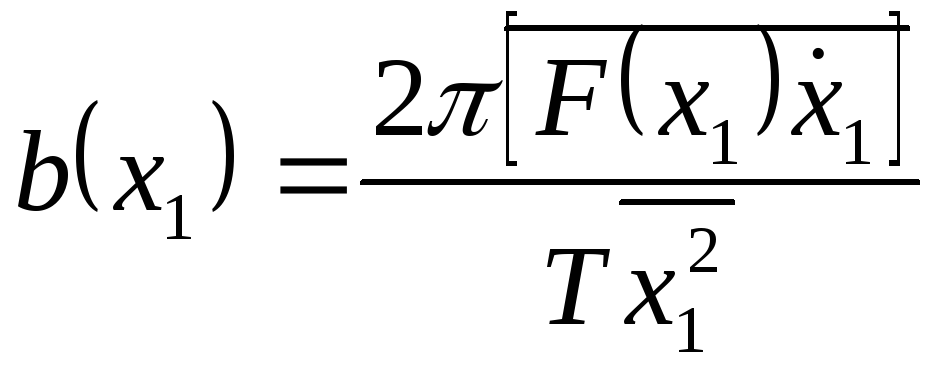. (62)

В данном примере входной сигнал запишем в виде:

, (63)

, (64)

. (65)

Когда для двузначной нелинейности общая эквивалентная функция:

. (66)