40) Тригонометрическая форма записи комплексного числа. Операции над комплексными числами в тригонометрической форме.

x = rcos , y = rsin

Z = x + iy = rcos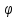 + irsin = r (cos) – тригонометрическая форма записи,

где r=|Z|= – модуль комплексного числа

= Аrg Z – аргумент комплексного числа

|Z|0

Аrg Z принимает множество значений, отличающихся на 2п

-пАrg Z п

Операции над комплексными числами в тригонометрической форме:

Пусть Z₁ = r₁(cos₁ + isin₁)

Z₂ = r₂(cos₂ + isin₂)

• Z₁ * Z₂ = r₁*r₂(cos() +isin())

• 

• ⁿ = rⁿ(cos(n) + isin(n)) – формула Муавра

• , k=0,1,…(n-1)