6. Найти частные производные первого порядка функции

Вариант №1.	Вариант № 2.
Вариант №3.	Вариант №4.
Вариант №5.	Вариант №6.
Вариант №7.	Вариант №8.
Вариант №9.	Вариант №10.
Вариант №11.	Вариант №12.
Вариант №13.	Вариант №14.
Вариант №15.	Вариант №16.
Вариант №17.	Вариант №18.
Вариант №19.	Вариант №20.
Вариант №21.	Вариант №22.
Вариант №23.	Вариант №24.
Вариант №25.	Вариант №26.
Вариант №27.	Вариант №28.
Вариант №29.	Вариант №30.

7. Исследовать на экстремум функцию z=z(x;y)

Вариант №1.	Вариант №2.
Вариант №3.	Вариант №4.
Вариант №5.	Вариант №6.
Вариант №7.	Вариант №8.
Вариант №9.	Вариант №10.
Вариант №11.	Вариант №12.
Вариант №13.	Вариант №14.
Вариант №15.	Вариант №16.
Вариант №17.	Вариант №18.
Вариант №19.	Вариант №20.
Вариант №21.	Вариант №22.
Вариант №23.	Вариант №24.
Вариант №25.	Вариант №26.
Вариант №27.	Вариант №28.
Вариант №29.	Вариант №30.

Методические указания к выполнению контрольной работы

I. Вычисление пределов

При вычислении пределов обычно используют следующие теоремы.

Предел суммы двух функций равен сумме пределов слагаемых, если пределы слагаемых существуют и конечны.

Предел произведения двух функций равен произведению пределов сомножителей, если пределы сомножителей существуют и конечны.

Предел частного равен частному от деления пределов, если пределы делимого и делителя существуют, конечны и предел делителя не равен нулю.

Т.е., если существуют конечные пределы и ,

то ,

,

, если .

Функции, полученные с помощью конечного числа операций сложения, умножения, деления, суперпозиции из основных элементарных

, называются элементарными.

Функция f(x) называется непрерывной в точке a, если и .

Все элементарные функции непрерывны в своей области определения, поэтому, если точка a принадлежит области определения элементарной функции f(x), то.

Пример 1. Вычислить предел .

.

Если предел одной или обеих функций равен бесконечности, то можно использовать соотношения:

, , ,

; ; ;

; .

Если при подстановке в функцию, стоящую под знаком предела, получается одна из следующих ситуаций , , , , , , , то говорят, что имеет место соответствующая неопределённость. Для раскрытия неопределённостей существуют специальные приёмы.

Например, если и неопределенность получена при делении многочленов, то для раскрытия неопределённости обычно делят числитель и знаменатель дроби на старшую степень переменной числителя или знаменателя.

Пример 2. Вычислить предел .

.

Здесь имелась неопределённость . Для её раскрытия мы разделили числитель и знаменатель на . А затем применили теорему о пределе частного. Предел каждой из «маленьких» дробей равен нулю, так как в их числителях стоят числа, а в знаменателях – бесконечно большие величины.

Пример 3. Вычислить предел .

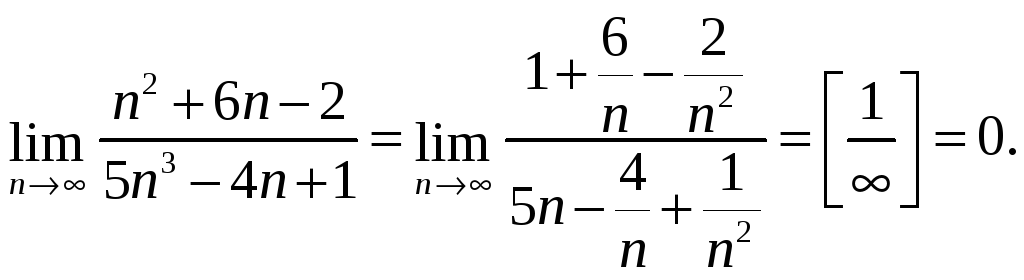
В этом примере мы делили на старшую степень числителя. Если бы мы разделили на старшую степень знаменателя, то получили бы

.

Пример 4. Вычислить предел .

Запись [ +0 ] означает, что в знаменателе стоит положительная бесконечно малая величина. Поэтому (+4)/(+0) = +.

Заметим, что считается, n всегда стремится к (+).

Если и неопределённость получается при делении многочленов, то числитель и знаменатель нужно разложить на множители, а затем сократить на ().

При этом нужно помнить, что квадратный трёхчлен раскладывается на множители следующим образом: , где и - корни квадратного трёхчлена. Их можно найти по формуле

.

Пример 5. Вычислить предел .

.

Если в числителе или знаменателе дроби есть разность квадратных корней, то можно умножить числитель и знаменатель дроби на сопряжённое выражение, т.е. на сумму этих же корней, а затем воспользоваться формулой разности квадратов:

Пример 6. Вычислить предел .

=

Если функция, стоящая под знаком предела, содержит тригонометрические или обратные тригонометрические функции, то можно использовать первый замечательный предел или следствия из него.

Кроме того, полезно вспомнить тригонометрические формулы:

cos 0 = 1, sin 0 = 0,

, ,

, ,

cos (-x) = cos x, sin(-x)=-sin(x),

,

.

Пример 7. Вычислить предел .

1

1

1

1

Пример 8. Вычислить предел .

1

.

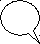
1

Для раскрытия неопределённости типа [] (и только такого типа) используется второй замечательный предел: , где е – число Непера, .

При решении примеров обычно используют следствия из второго замечательного предела: или .

Пример 9. Вычислить предел .

Следовательно, имеем неопределенность []. Выделим внутри скобки единицу:

Здесь при , т.е. является бесконечно малой величиной при .

Для использования второго замечательного предела нужно, чтобы в показателе стояла величина обратная этой бесконечно малой .

При возведении в степень показатели перемножаются, поэтому полученное выражение нужно возвести в степень (-4)/(2x+1), тогда выражение под знаком предела в результате наших преобразований не изменится. Необходимо не забыть о прежнем показателе степени. Итак,

=.

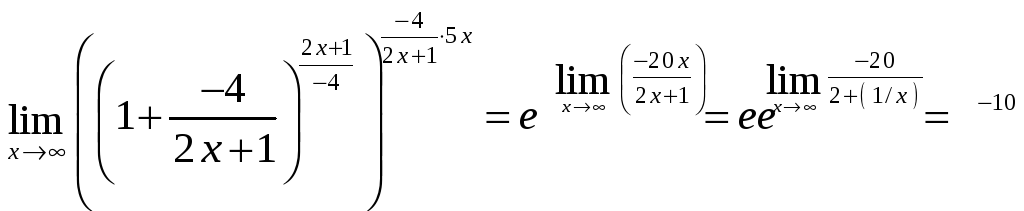Пример 10. Вычислить предел .

.