2.3.1.2. Скейлинг (масштабное преобразование) и стандартизованное расстояние

В общем случае значения существенных признаков, подаваемые на вход системы классификации, являются размерными величинами. Например, это может быть сила тока, измеряемая датчиком в некоторых единицах, предположим в амперах. Следовательно, в этом случае и расстояния между объектами и центрами классов будут измеряться в амперах. Дисперсия тогда будет измеряться в , а среднеквадратичное отклонение в амперах. Если же значения существенных признаков измеряются в вольтах, то в тех же единицах будут измеряться и расстояние, среднее значение и среднеквадратичное отклонение.

Чтобы сделать расстояние безразмерной величиной, т.е. не зависящей от единицы измерения существенных признаков, произведем масштабное преобразование расстояния. Для этого разделим обычное расстояние на среднеквадратичное отклонение :

. (2.11)

Безразмерная величина называется стандартизованным расстоянием.

Приведем в развернутом виде формулу для вычисления стандартизованного расстояния между объектом и некоторым классом

.(2.11а)

Здесь компоненты среднеквадратического отклонения для класса определяются по формуле

,

где - дисперсия -го признака объектов принадлежащих классу , - количество объектов в данном классе.

Для иллюстрации понятия скейлинга рассмотрим следующий пример. Более характерной для скейлинга является следующая ситуация. Предположим, что системе для распознавания предъявлены три треугольника - , и . Причем вследствие, например, ошибок измерения длины сторон этих треугольников принимают следующие значения: , и . Очевидно, что эти треугольники подобны и могут быть отнесены к одному и тому же классу. Но, поскольку, они имеют разные длины сторон, эти треугольники могут, при определенных условиях, восприниматься системой классификации как объекты, принадлежащие разным классам. С другой стороны, необходимо использовать, в определенной степени, сложные решающие правила, учитывающие подобие треугольников. Чтобы в данной ситуации упростить процедуру классификации и сделать ее более надежной, поступим следующим образом: выберем в каждом треугольнике наибольшую сторону, а затем разделим все его стороны на наибольшую. В результате получим треугольники со сторонами: , и . Таким образом, после выполненного масштабного преобразования имеем три равных треугольника.

2.3.1.3 Ковариационная матрица

Ковариация – это численное выражение свойства ковариантности двух существенных признаков объектов. Свойство ковариантности означает, что признаки имеют тенденцию изменяться совместно (ковариантно). В этом случае, говорят еще, что признаки коррелируют.

Пусть, например, к некоторому классу принадлежат три объекта: , , . Как видно, при переходе от первого объекта к третьему значения первого и второго существенных признаков возрастают, то есть признаки изменяются совместно или ковариантно. Аналогичная ковариантность признаков будет наблюдаться и в таком случае , , . Здесь первый признак возрастает, а второй убывает, однако между ними также существует сильная корреляция. Если же существенные признаки объектов имеют, например, такие значения , , , то они не коррелируют между собой и, следовательно, изменяются не ковариантно.

Ковариационная матрица состоит из ковариаций между всеми парами существенных признаков объектов, относящихся к одному классу. Пусть количество существенных признаков равно . Тогда ковариационная матрица – это матрица размерности , имеющая вид:

.

Элементы ковариационной матрицы – ковариации – для объектов -того класса вычисляются по формуле:

, (2.12)

где - номер объекта данного класса, и - номера признаков, а -номер класса, и - множества, состоящее из значений соответственно -го и -го существенных признаков (напомним, что -количество объектов в данном классе); и - средние значения соответственно -го и -го существенных признаков (см. формулу (2.8)).

Ковариации обладают следующими важными свойствами:

• если при переходе от одного объекта класса к другому -ый и -ый существенные признаки увеличиваются вместе, то ;

• если при переходе от одного объекта класса к другому -ый существенный признак уменьшается, а -ый увеличивается, то ;

• если при переходе от одного объекта класса к другому -ый и -ый существенные признаки изменяются независимо, то ;

• , где и – стандартные отклонения -го и -го существенных признаков соответственно (формула (2.10));

• , где – стандартное отклонение и 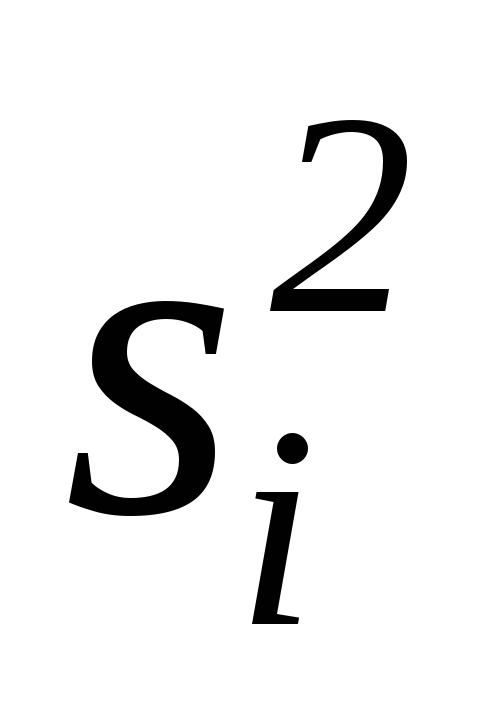– дисперсия -го существенного признака.

Т аким образом, ковариация представляет собой число в интервале , которое является мерой корреляции между -ым и -ым существенными признаками, причем, , если -ый и -ый существенные признаки независимы. Соответствие между ковариацией и формой класса объектов показано на рис. 2.11.

Отметим, что ковариационная матрица будет вырожденной в следующих двух случаях:

1. Если количество объектов в данном классе меньше, чем количество существенных признаков плюс 1, т.е. .

2. Если степень корреляции существенных признаков максимальна, т.е. .

В этих двух случаях нельзя обратить матрицу и расстояние следует вычислять по формуле стандартизованного расстояния .