Алгоритм изодата

ИЗОДАТА (по-английски ISODATA) означает «Итерационные самоорганизующиеся методы анализа данных». Это более сложный и гибкий алгоритм, чем рассмотренные ранее алгоритмы Максимина и К-средних. В частности, в отличие от алгоритма К-средних, количество классов здесь не фиксировано и может автоматически изменяться в процессе выполнения алгоритма путем объединения подобных классов и разбиения классов с большими среднеквадратичными отклонениями. Существенной особенностью алгоритма ИЗОДАТА является то, что здесь можно произвольно выбирать пороги для объединения и разбиения классов, а также ряд других параметров. Это позволяет проводить более гибкую и точную процедуру классификации, многократно выполняя вычисления и выбирая те значения параметров, которые обеспечивают наилучший результат. Отметим также, что алгоритм ИЗОДАТА предназначен для «четкой» классификации, т.е. может применяться, когда выборка объектов разделяется на сепарабельные классы в пространстве существенных признаков. В случае несепарабельных классов, т.е. в случае, когда между классами нельзя провести четкие границы, следует применять алгоритмы «нечеткой» классификации, например, нечеткий алгоритм К-средних. Область применения алгоритма ИЗОДАТА не ограничивается только распознаванием образов. Благодаря тому, что с его помощью можно легко обрабатывать большие массивы исходных данных, этот алгоритм используют для широкого класса практических задач в области метеорологии, социологии, медицины, биологии и т.д.

В алгоритме ИЗОДАТА используется ряд параметров, которые следует задать перед вычислениями:

– желательное количество классов, которое определяется на основе предварительного анализа совокупности объектов. Если такой анализ провести невозможно или очень сложно ввиду большого объема выборки, то значение можно выбрать произвольно. В ходе выполнения алгоритма ИЗОДАТА количество классов будет уточняться.

– максимальное количество итераций; этот параметр ограничивает количество итераций, которое может быть выполнено при работе алгоритма и позволяет ограничить время выполнения алгоритма в случае медленной сходимости, то есть когда для классификации объектов необходимо выполнить такое большое количество итераций, что затраты времени становятся неприемлемыми. Переменная хранит текущее количество выполненных итераций. Начальное значение этой переменной

- максимальное количество пар классов, которые могут быть объединены; этот параметр ограничивает «сверху» процедуру объединения классов, т.е. позволяет избежать ситуации, при которой количество классов на -той итерации оказывается существенно меньше желательного количества классов .

- минимальное количество объектов, которое может содержаться в классе; если в процессе итерации в каком либо классе окажется меньше, чем объектов, то этот класс удаляется. Таким образом, параметр используется для предотвращения ситуации, при которой пространство существенных признаков будет разбито на слишком маленькие классы.

- пороговое значение для среднеквадратичного отклонения, которое используется для разбиения классов.

- пороговое значение для расстояний между центрами классов, которое используется для объединения классов.

- весовой множитель для среднеквадратичного отклонения ; этот параметр используется для вычисления новых положений центров классов при разбиении класса с большим среднеквадратичным отклонением объектов от центра класса на два новых класса.

- метрика для вычисления расстояний в пространстве существенных признаков.

Выбор вышеперечисленных параметров в значительной степени эмпирический. Он основывается как на предварительном анализе массива исходных данных, так и на анализе самих результатов применения алгоритма. Если эти результаты оказались неудовлетворительными, следует по возможности выяснить, значение какого из параметров привело к таким результатам, изменить это значение и повторно выполнить алгоритм. Таким образом, многократно выполняя вычисления при различных значениях параметров, как правило, удается получить надежные результаты классификации объектов с помощью алгоритма ИЗОДАТА.

Словесное описание алгоритма

1. Произвольно выбираем начальных положений центов классов , используя массив исходных данных , где – количество объектов в выборке. При этом значение 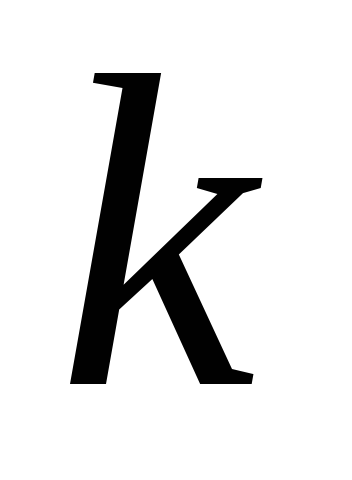не обязательно равно значению параметра . Выбор начальных положений центров классов выполняется так же, как и в алгоритме К-средних: в качестве можно выбрать первых объектов выборки, либо случайным образом выбрать произвольных объектов.

2. Группируем объекты вокруг центров классов. Этот шаг также аналогичен соответствующему шагу алгоритма К-средних. Вычисляем в выбранной метрике расстояние между центрами классов и объектами выборки . Отметим, что если некоторые объекты на данной итерации являются центрами классов, то расстояния между ними вычислять не нужно. Следовательно, как и в простом алгоритме К-средних, на каждой итерации нужно отмечать объекты, являющиеся в данный момент центрами классов, и вычислять расстояния только между центрами классов и непомеченными объектами. Затем для каждого из объектов находим минимальное расстояние и относим объект к соответствующему классу: если , где через обозначен -ый класс.

3. Удаляем классы, количество объектов в которых меньше чем , т.е. если для некоторого , то удаляем класс и уменьшаем значение на единицу .

4. Вычисляем новые положения центров классов как среднее арифметическое векторов, принадлежащих одному классу:

.

Здесь для каждого суммирование производится только по объектам, принадлежащих данному -му классу . Таким образом, вычисления положений центров классов в алгоритме ИЗОДАТА производится по той же формуле, что и в простом алгоритме К-средних.

5. Для всех классов вычисляем среднее расстояние от центра класса до всех объектов, относящихся к данному классу:

.

5. Вычисляем взвешенное среднее расстояние объектов классов от их центров:

Весовым множителем в этой сумме является количество объектов в данном классе .

5. На этом шаге алгоритм разветвляется и требуется принять решение, по какой из двух ветвей следует производить дальнейшие вычисления. Одна из ветвей – шаги с 8-го по 10-ый - реализует разбиение классов с большими среднеквадратичными отклонениями объектов от центров классов, а другая ветвь – шаги с 11-го по 13-ый - реализует объединение подобных классов, т.е. классов, расстояния между центрами которых меньше выбранного порогового значения .

Критерий выбора одной из ветвей для дальнейших вычислений также является эмпирическим. Очевидно, что нужно сравнить количество имеющихся на данный момент классов с желательным количеством классов . При этом ясно, что если , то классов слишком мало и нужно увеличивать их количество, т.е. разбивать большие классы, а если , то классов слишком много и нужно объединять подобные классы. Однако, для принятия решения в алгоритме вышеназванные условия нужно конкретизировать. В общем случае выберем их следующим образом: если , то классы следует разбивать, а если , то классы следует объединять, если же , то количество классов следует оставить неизменным и перейти к следующей итерации. Здесь и – некоторые параметры, удовлетворяющие условиям и , определяющие диапазон для количества классов.

Выберем и . Таким образом, разбиение классов будем производить, если их в два и более раз меньше, чем желательно, а объединение – если их в два и более раз больше.

Итак, сформулируем окончательно решающее правило.

Если то перейти к шагу 8., иначе перейти к шагу 11.

Если то перейти к шагу 14.

5. Для того чтобы некоторый класс подходил для разбиения его на два класса, должны удовлетворяться одновременно три условия. Первое условие требует, чтобы максимальное среднеквадратичное отклонение объектов этого -го класса от его центра было больше установленного порога : . Второе условие требует, чтобы среднее расстояние от центра -го класса было больше взвешенного среднего расстояния : . Это условие означает, что данный класс имеет в пространстве существенных признаков размер, больший среднего размера класса для данной выборки объектов. И наконец, третье условие требует, чтобы в классе было больше объектов, чем минимально допустимое количество объектов в классе : , где c – некоторая константа, большая единицы. В дальнейшем будем считать, что . Подчеркнем, что только при выполнении всех трех из вышеперечисленных условий класс подходит для разбиения на два новых класса.

Таким образом, для принятия решения о разбиении некоторого -го класса нужно знать следующие три величины: максимальное среднеквадратичное отклонение объектов этого класса от его центра , среднее расстояние от объектов класса до его центра и взвешенное среднее расстояние для всей выборки D (остальные величины являются задаваемыми параметрами). Величины и уже вычислены в ш. 5 и ш. 6 соответственно. Теперь нужно вычислить максимальное среднеквадратичное отклонение. Для этого находим вектор среднеквадратичного отклонения для каждого класса (). Нижний индекс в – это номер существенного признака, n – их количество, а верхний индекс – это номер класса. Таким образом, размерность (количество компонент) вектора равно количеству существенных признаков объектов и совпадает с размерностью вектора – положения центра класса. Среднеквадратическое отклонение вычисляется следующим образом: -я компонента для -го класса (среднеквадратичное отклонение объектов класса по -ой координатной оси) вычисляется по формуле:

, .

Здесь - -ая компонента вектора - центра класса; - -ая компонента объекта ; для каждого класса суммирование производится только по объектам, принадлежащим данному классу .

Шаг 9. Находим максимальный из компонентов вектора и обозначаем его . Таким образом, из совокупности среднеквадратичных отклонений для разных существенных признаков выбирается максимальное. Эту операцию следует выполнить для всех классов .

Шаг 10. Теперь все величины, необходимые для принятия решения о разбиении классов, вычислены.

Если для какого-либо истинны все следующие условия:

,

,

,

тогда разбиваем класс на два новых класса. Центры этих двух классов вычисляются по формулам:

,

,

где - некоторый заранее заданный параметр. После этого удаляем старый центр класса (после разбиения класса на два новых старый класс больше не существует) и увеличиваем значение на единицу: . После того как все пригодные для разбиения классы будут разделены на два новых, полагаем (увеличиваем количество итераций на единицу) и переходим к шагу 2.

Если не существует такого , для которого все три вышеперечисленных условия истинны, то переходим к шагу 14.

Шаг 11. С этого шага начинается процедура объединения подобных классов. Под подобными здесь понимаются классы, находящиеся ближе всего друг к другу в пространстве существенных признаков. Чтобы найти такие классы, следует вычислить расстояния между всеми центрами классов, а затем выбрать из найденных расстояний некоторое количество наименьших. Количество классов с наименьшими расстояниями регулируется двумя параметрами: пороговым значением и максимальном количеством объединяемых пар классов . Первый из этих параметров определяет степень близости объединяемых классов, т.е. объединяются попарно только те классы, расстояние между центрами которых меньше . Второй параметр ограничивает «сверху» количество объединяемых классов. Такое ограничение необходимо для того чтобы предотвратить ситуацию, при которой количество классов на данной итерации оказывается существенно меньше желательного количества классов . Эта ситуация может возникнуть в случае, если для параметра выбрано слишком большое значение и количество классов подлежащих объединению будет больше чем это необходимо (то есть в эту категорию попадут классы, которые не следует объединять).

Вычисляем расстояния между всеми центрами классов:

для всех ,

а затем упорядочиваем эти найденные расстояний в порядке возрастания.

Шаг 12. После того, как расстояния между центрами классов упорядочены, выбираем из них те, которые меньше порога . Далее, из этих расстояний нужно выбрать те, которые соответствуют неповторяющимся классам и определить их количество . Этот этап необходим потому, что классы объединяются попарно, т.е. некоторый класс можно объединить только с другим классом, а именно с тем, расстояние до центра которого минимально. Если , то объединению подлежат все неповторяющиеся пары классов, для которых . Если же , то из найденных соответствующих неповторяющимся классам, следует отобрать наименьших.

Проиллюстрируем сказанное примером. Пусть количество классов , а расстояния между центрами классов в выбранной метрике: , , , , , , , , , . Параметры и имеют следующие значения: , . Упорядочим в порядке возрастания: , , , , , , , , , .

Условию удовлетворяют первые восемь расстояний. Отберем из них те, которые соответствуют неповторяющимся классам, просматривая список слева направо, т.е. в порядке возрастания расстояний. Первым в списке стоит . Далее идет , но 3-ий класс уже использован, он будет объединяться с 1-ым классом, значит пропускаем. Рассуждая далее аналогичным образом, находим, что из списка следует выбрать еще расстояние . Таким образом , а соответствующие расстояния и .

Сравним с параметром . При , , следовательно из двух подходящих для объединения пар классов – 1-ый с 3-им и 4-ый с 5-ым – нужно выбрать только одну пару, а именно ту, для которой расстояние между центрами классов минимально. Таким образом, объединить нужно 1-ый 3-ий классы.

Шаг 13. Объединяем классы попарно. Для вычисляем положения новых центров по формуле:

.

Здесь индекс указывает на номер объединяемой пары классов, а индексы и номера объединяемых классов. и - количества объектов в -ом и -ом классе соответственно, которые образуют -ую объединяемую пару; и - центры классов.

Так, для вышеприведенного примера, где объединяется только одна пара классов, , , , положение нового центра будет вычисляться по формуле:

,

где и - количества объектов в 1-ом и 3-ем классе соответственно, а и - их центры.

Затем следует удалить все старые центры объединенных классов (после объединения эти классы больше не существуют), т.е. удалить все и для . Уменьшить количество классов на : . После этого полагаем (увеличиваем количество итераций на единицу) и переходим к шагу 2.

Шаг 14. Заканчиваем вычисления, если достигнуто максимальное число итераций . Иначе увеличиваем на единицу счетчик итераций и выполняем следующую итерацию, т.е. полагаем и переходим к шагу 2.

Дополнить разделами

1. Вероятностный подход определения существенных признаков.

3. Распознавание сигналов. Оконные функции.

Литература

Р1. Bow S.T. Pattern recognition, Marcel Dekker Edit, Electrical Engineering and Elektronic series, 23, 1984, p. 30-32.