- •14. Решите общую задачу о сроке увеличения вклада в n раз при данной процентной ставке I в случае сложных процентов.
- •22. Выведите формулы для коэффициентов приведения и наращения
- •23.Пусть известны n, I, r. Найдите наращенную сумму s и приведенную величину a годовой ренты. Приведите пример.
- •24.Пусть известны a, I, r. Найдите срок ренты n. Приведите пример.
- •29. Вывести формулы для приведенной и наращенной величины р-срочной ренты постнумерандо.
- •30. Напишите формулы для приведенной величины и наращенной сумм p-срочной ренты постнумерандо в случае k-кратного начисления процентов. Приведите пример ее применения.
- •31. Во сколько раз больше будет наращенная сумма в конце n–ого периода при ежепериодном (в конце периода) платеже r, чем при разовом платеже r в начальный момент времени?
- •37. Дайте определение и приведите пример выкупа ренты.
- •38. Дайте определение и приведите пример консолидации рент.
- •39. Дайте определение и приведите пример рассрочки платежа.
- •44. Сформулируйте правила Вальда, Сэвиджа, Гурвица. Приведите
- •45. Выведите формулу доходности портфеля из n бумаг через доходности отдельных бумаг.
- •46. Как определяется доходность и риск портфеля из n бумаг?
- •53. Выведите уравнение минимальной границы.
- •54. Доказать, что уравнение минимальной границы является ветвью
- •55. Найдите портфель Марковица минимального риска при заданной
- •56. Опишите портфель Тобина.
- •57. Докажите, что прямая является касательной к графику минимальной границы.
- •63. Какова связь рыночной цены облигации с ее номинальной стоимостью
- •64. Проанализируйте зависимость доходности к погашению облигаций
- •65. Докажите, что относительное изменение цены облигации (в процентах) в результате изменения доходности к погашению будет тем меньше, чем выше купонная ставка.
- •72. Какова связь между дюрацией портфеля облигаций и дюрациями отдельных облигаций данного портфеля.
- •73. Дайте определение и приведите формулу для выпуклости портфеля облигаций
1.Докажите, что при одной и той же ставке процента наращение по схеме простых процентов является более выгодным для периода наращения менее года, а для периода наращения более года более выгодным является наращение по схеме сложных процентов.
1)Прост.проц: St=S0(1+it)
Слож.проц:
St=S0(1+i)t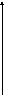

St 
S0(1+i)

S0

1 t
Следовательно, в пределах года простое исчисление выгоднее.
2)Пусть
срок вклада- n
лет. Тогда при начислении сложн.проц:
St=S0(1+i)t,
а при исчислении прост.проц.: St=S0(1+it).
Раскроем (1+i)t
по формуле бинома Ньютона: (1+i)t=
1+it+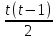 *i2+…+it
>1+it
при t
>1.
*i2+…+it
>1+it
при t
>1.
Если больше года, то сложное исчисление выгоднее.
2.Выведите формулу для наращенной суммы при непрерывном начислении процентов в случае простых процентов.
Если частота начисления процентов N неограниченно возрастает:
St=
 0(1+
0(1+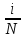 Nt)
= S0
(1+it)
Nt)
= S0
(1+it)
3. Выведите формулу для наращенной суммы при непрерывном начислении процентов в случае сложных процентов.
St= 0(1+
0(1+
 )Nt
=S0
)Nt
=S0
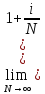 )N/t
]it
=S0eit
)N/t
]it
=S0eit
i заменяется на б-сила роста.
St=S0etб
4.Выведите эффективную процентную ставку в случае простых процентов
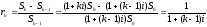
уменьшается с увеличением k
5. Выведите эффективную процентную ставку в случае сложных процентов (3 случая)
за n-й период начисления:
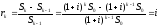 не
зависит от k
и равна номинальной
не
зависит от k
и равна номинальной
кратное начисление процентов:

для непрерывных процентов:
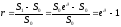
6.(7,8,9)Эквивалентность различных процентных ставок
Ставки называются эквивалентными, если они имеют одинаковые коэффициенты роста
Эквивалентность простых и сложных процентов
is – простая процентная ставка, id – сложная процентная ставка,
ic – непрерывная процентная ставка
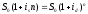
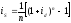
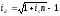
Эквивалентность простых и непрерывных процентов
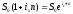

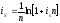
Эквивалентность сложных и непрерывных процентов
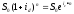
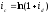
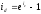
10. Выведите “Правило 70” в случае сложных процентов.
2So=So(1+i)^t
Ln2=t ln (1+i)
Ln(1+i)=i
Ln2=ti
T=ln2/i
11. Выведите “Правило 70” при кратном начислении процентов в случае сложных процентов.
2So=So(1+i/m)^tm
2= (1+i/m)^mt
Ln 2=mtln(1+i/m)
Ln(1+i/m) = i/m
Ln2=mt(i/m)
Ln2=ti
T=ln2/i
12. Выведите “Правило 70” при непрерывном начислении процентов в случае сложных процентов.
2So=So(e^ti)
2=e^ti
Ti=ln2
T=ln2/i
13. Выведите “Правило 100”.
Это правило позволяет ответить на вопрос : за сколько лет удвоится вклад, помещенный в банк под i процентов годовых?
«правило 100» используется в случае простых процентов
2So = S0(1+Ti)
Ln2 = Ln (1+Ti)
2 = 1+Ti, откуда T=1/i, или (если I выражена в процентах): T=100/ I (за T=100/ i примерно происходит удвоение капитала в схеме простых процентов при ставке i, ставка задается в процентах)
Пример : за сколько лет удвоится капитал в схеме простых процентов
При ставе 18 % годовых?
T= 100/ i = 100/18 = 5,56 лет
14. Решите общую задачу о сроке увеличения вклада в n раз при данной процентной ставке I в случае сложных процентов.
Это правило можно получить из формулы сложных процентов .
nSo = So (1+ i)^ T
Ln n = Ln (1+i)
Разлагая Ln (1+i) по степеням I, получим Ln(1+i) ≈i. Следовательно, Ln n ≈ iT, откуда
T=Ln n/i.
Учёт следующего (квадратичного) по i члена в разложении Ln(1+i) ≈ I-i²/2 дает результат
T≈ ln n / i (1- i/2) увеличивающий срок роста капитала в n раз T≈ ln n / i (1+ i/2) на
ΔT≈ ln n / 2
Таким образом, при рассмотрении задачи об увеличении капитала в произвольное число раз (n) в схеме мложных процентов при данной процентной ставке I необходимо в «Правиле 70» лишь сделать замену
Ln 2 —> Ln n
15. Решите общую задачу о сроке увеличения вклада в n раз при данной процентной ставке i в случае простых процентов.
В случае простых процентов имеем
nS0 = S0(1+Ti)
отсюда n = 1+Ti, откуда T= (n-1)/i
Например, при ставке 10 5 годовых вклада вырастет в 4 раза за T = (n-1)/i= 3/0,1=30 лет
16. Решите общую задачу о сроке увеличения вклада в n раз при данной процентной ставке i в случае кратного начисления сложных процентов.
Увеличение капитала в n раз
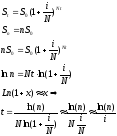
Если
используется приближение
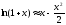 ,
то
,
то
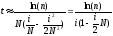
При
N=1

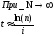
17. Решите общую задачу о сроке увеличения вклада в n раз при данной процентной ставке i в случае непрерывных процентов.
1)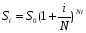 2)
2)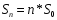 3)
3)

4)
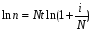 5)
5)

6)
А
т.к.
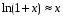 и
и
 то
то
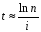
18. Выведите формулу Фишера.
α – уровень инфляции (стоимость товаров увеличивается в (1+α) раз)
Деньги обесцениваются в (1+α) раз
S0,
S1=S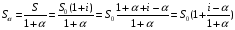
Реальная сумма:
iα – процентная ставка с учетом инфляции
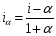
Формула Фишера:
α – мало => i2 = i - α
19.Темпы
инфляции за последовательные периоды
времени
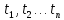 равны
соответственно
равны
соответственно
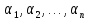 .
Найдите темп инфляции за период
.
Найдите темп инфляции за период
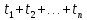
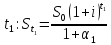
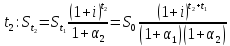
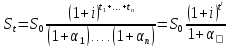

Если
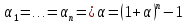
n=2

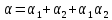 -
синергетический эффект
-
синергетический эффект
20.Дайте определение и выведите формулу для среднего срока финансового потока
Определение: средним сроком денежного потока относительно ставки дисконтирования i называется момент времени t, такой что S(t) = C1+C2+…+Cn.
CF = {(t1, C1),…,(tn,Cn)}
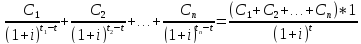 =
=
 +
+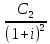 +…+
+…+
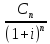 =
=
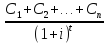 = C1(1+i)-t1
+ C2(1+i)-t2
+…+
Cn(1+i)-tn
= (C1+C2+…+Cn)*(1+i)-t
= C1(1-t1i)
+ C2(1-t2i)
+…+Cn(1-tni)
= (C1+C2+…+Cn)(1-ti)
= i(C1t1
+
C2t2+…+Cntn)
≈ i(C1+C2+…+Cn)t
= C1(1+i)-t1
+ C2(1+i)-t2
+…+
Cn(1+i)-tn
= (C1+C2+…+Cn)*(1+i)-t
= C1(1-t1i)
+ C2(1-t2i)
+…+Cn(1-tni)
= (C1+C2+…+Cn)(1-ti)
= i(C1t1
+
C2t2+…+Cntn)
≈ i(C1+C2+…+Cn)t
t
≈

21.Дайте определение внутренней нормы доходности. Исследуйте зависимость чистого приведенного дохода (NPV) от ставки приведения (принятой нормы доходности) i. Приведите качественный график данной зависимости.
Внутренняя норма доходности ( IRR ) — это процентная ставка, при которой чистый дисконтированный доход (NPV) равен 0. NPV рассчитывается на основании потока платежей, дисконтированного к сегодняшнему дню.
Иначе говоря, для потока платежей CF, где CFt — платёж через t лет (t = 1,...,N)
Ск – баланс инвестиционных затрат и чистого дохода за к-ый период.
NPV(i)=
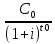 +
+
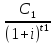 +…+
+…+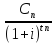
NPV(i)>0 → доходы окупают расходы
NPV<0 → доходы не окупают расходы
Рассмотрим CF ={ (0;-к), (1;С1), (2;С2),…, (n;Cn)}, k>0, Ck>0, ᴲk: Ск>0
NPV(i)
= -k +
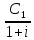 +
+
 +…+
+…+