7. Уравнения максвелла

• Полный ток, определяющий магнитное поле в веществе:

,

где вектор электрического смещения.

В зависимости от электропроводности среды и частоты (поля) оба слагаемых играют разную роль:

• в металлах и на низких частотах 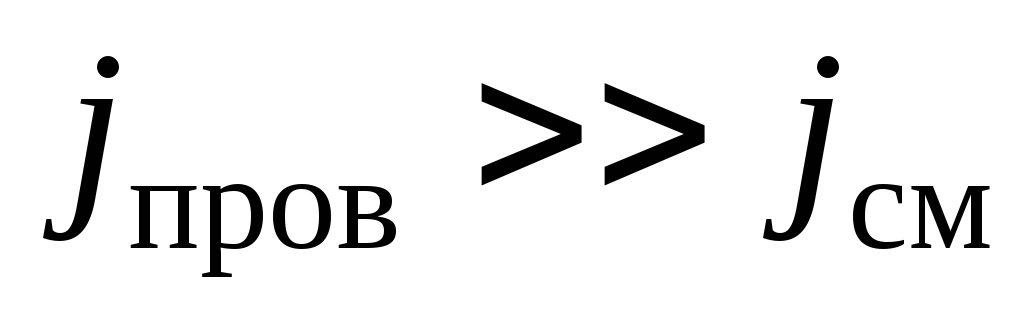(в скин-эффекте не играет заметной роли);

• в диэлектриках и на высоких частотах играет основную роль.

• Плотность тока смещения:

,

где – плотность тока смещения в вакууме; – плотность тока поляризации.

• Полная система уравнений Максвелла:

• в интегральной форме:

, ,

, ;

• в дифференциальной форме:

, ,

,

• Уравнения состояния или материальные уравнения (определяются электрическими и магнитными свойствами среды):

,

здесь σ – удельная проводимость, – плотность сторонних токов.

5. Колебания и волны. Геометрическая и волновая оптика

1. Гармонические колебания

• Уравнение гармонических колебаний:

где х – смещение колеблющейся величины от положения равно­весия; А – амплитуда колебаний

• Гармонические колебания в графическом виде:

• Частота колебаний – число последовательных колебаний в одну секунду:

.

• Циклическая (круговая) частота колебаний – число полных колебаний за 2π секунд:

.

• Период колебаний – минимальный промежуток времени, по истечению которого повторяются значения всех физических величин, характеризующих колебания:

.

• Скорость колебаний:

.

• Ускорение колебаний:

.

• Амплитуда скорости:

.

• Амплитуда ускорения:

.

• Уравнение движения материальной точки:

.

• Квазиупругая сила:

.

• Дифференциальное уравнение динамики гармонических колебаний материальной точки под действием упругих и квазиупругих сил:

или .

• Циклическая частота незатухающих колебаний:

.

• Период незатухающих колебаний:

.

• Потенциальная энергия Е_п тела:

.

• Кинетическая энергия тела:

.

• Полная механическая энергия материальной точки, совершающей гармонические колебания:

.

• Математический маятник – идеализированная система, состоящая из невесомой нерастяжимой нити, на которую подвешена масса, сосредоточенная в одной точке (шарик на длинной тонкой нити).

• Уравнение динамики вращательного движения математического маятника:

.

• Вращающий момент стремится вернуть маятник в положение равновесия, он возникает при отклонении тела от положения равновесия на угол α:

,

где l – расстояние между точкой подвеса и центром масс маятника С.

• Момент инерции маятника:

.

• Угловое ускорение:

.

• Дифференциальное уравнение математического маятника:

;

• решение данного уравнения:

.

• Циклическая частота математического маятника:

.

• Период колебаний математического маятника:

• в инерциальной системе отсчета:

;

• в неинерциальной системе отсчета:

• Циклическая частота физического маятника физический маятник – (это твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной оси, проходящей через точку О, не совпадающие с центром масс С):

.

• Период колебаний физического маятника:

.

• Приведенная длина физического маятника:

.