
- •§ 8.1. Склад і характеристики ядра 84
- •§ 8.2. Дефект маси та енергія зв’язку ядра. Ядерні сили 86
- •§ 4.1. Магнітне поле і його характеристики. Дія магнітного поля на контур зі струмом. Принцип суперпозиції. Класифікація магнетиків
- •§ 4.2. Закон Біо – Савара – Лапласа. Магнітне поле прямолінійного та колового струмів
- •§ 4.3. Циркуляція вектора напруженості магнітного поля. Вихровий характер магнітного поля. Поле довгого соленоїда
- •§ 4.4. Дія магнітного поля на струм; сила Ампера. Магнітна взаємодія струмів
- •§ 4.5. Сила Лоренца. Рух електричних зарядів в магнітному полі
- •§ 4.6. Магнітний потік. Теорема Гауса для магнітного поля
- •§ 4.7. Робота переміщення провідника та контура зі струмом в магнітному полі
- •§ 4.8. Явище електромагнітної індукції. Закон Фарадея. Правило Ленца
- •§ 4.9. Індуктивність контура. Явище самоіндукції. Енергія магнітного поля
- •§ 4.10. Магнітне поле в речовині
- •§ 4.11. Вихрове електричне поле
- •§ 4.12. Струми зміщення. Теорема про циркуляцію вектора напруженості магнітного поля (закон повного струму)
- •§ 4.13. Система рівнянь Максвелла. Електромагнітне поле
- •§ 5.1. Гармонічні коливання. Диференціальне рівняння гармонічних коливань та його розв’язок. Амплітуда, фаза, частота, період коливань
- •§ 5.2. Математичний маятник
- •§ 5.3.Фізичний маятник
- •§ 5.4. Енергія гармонічних коливань
- •§ 5.5. Додавання однаково направлених гармонічних коливань однакової частоти
- •§ 5.6. Додавання взаємно перпендикулярних коливань
- •§ 5.7. Згасаючі коливання
- •§ 5.8. Вимушені коливання
- •§ 5.9. Поняття хвилі, рівняння хвилі. Поздовжні і поперечні хвилі. Фронт хвилі і хвильові поверхні. Довжина хвилі, хвильове число, фазова швидкість.
- •§ 5.10. Хвильове рівняння
- •§ 5.11. Енергія пружної хвилі
- •§ 5.12. Групова швидкість і дисперсія хвиль
- •§ 5.13. Стоячі хвилі
- •§ 5.14. Електромагнітні коливання
- •§ 5.15. Вимушені електромагнітні коливання
- •§ 5.16. Електромагнітні хвилі. Шкала електромагнітних хвиль
- •§ 5.17. Енергія електромагнітних хвиль. Вектор Умова-Пойнтінга
- •Розділ 6. Оптика.
- •§ 6.1. Елементи геометричної оптики: закони відбивання і заломлення світла; тонкі лінзи
- •§ 6.2. Монохроматичні світлові хвилі
- •§ 6.3. Інтерференція світла
- •§ 6.4. Інтерференція світла на тонких плівках
- •§ 6.5. Дифракція світла. Принцип Гюйгенса - Френеля. Метод зон Френеля
- •§ 6.6. Дифракція Фраунгофера
- •§ 6.7. Дифракція рентгенівських променів
- •§ 6.8. Поляризація світла. Типи і способи поляризації
- •§ 6.9. Інтерференція поляризованих променів. Обертання площини поляризації
- •§ 6.10. Дисперсія світла
- •§ 6.11. Квантова природа випромінювання. Теплове випромінювання
- •§ 6.12. Фотоефект
- •§ 6.13. Тиск світла
- •§ 6.14. Ефект Комптона
- •§ 6.15. Гальмівне рентгенівське випромінювання
- •§ 7.1. Ядерна модель атома. Борівський воднеподібний атом. Спектральні серії
- •§ 7.2. Корпускулярно-хвильовий дуалізм матерії; гіпотеза де Бройля. Співвідношення невизначеностей Гайзенберга
- •§ 7.3. Хвильова функція та її зміст. Рівняння Шредінгера
- •§ 7.4. Частинка в одновимірній прямокутній потенціальній ямі. Проходження частинки через потенціальний бар’єр
- •§ 7.5. Квантовий лінійний гармонічний осцилятор
- •§ 7.6. Воднеподібні атоми в квантовій механіці. Квантові числа
- •§ 7.7. Магнітний момент атомів. Досліди Штерна і Герлаха. Власний момент електрона (спін). Ферміони і бозони
- •§ 7.8. Принцип Паулі. Стани електронів в складних атомах
- •§ 7.9. Характеристичне рентгенівське випромінювання
- •§ 7.10. Енергія молекул. Молекулярні спектри
- •§ 7.11. Люмінесценція
- •§ 7.12. Поглинання, спонтанне і вимушене випромінювання. Квантові генератори
- •§ 7.13. Теплові коливання кристалічної гратки і теплоємність твердих тіл
- •§ 7.14. Елементи зонної теорії твердих тіл
- •§ 7.14.2. Розподіл частинок з напівцілим спіном (ферміонів), в т.Ч. І електронів, за енергіями описується квантовою функцією розподілу Фермі-Дірака
- •§ 7.15. Електропровідність металів і напівпровідників
- •§ 7.16. Напівпровідникові структури
- •§ 8.1. Склад і характеристики ядра
- •§ 8.2. Дефект маси та енергія зв’язку ядра. Ядерні сили
- •§ 8.3. Радіоактивність
- •§ 8.4. Ядерні реакції
- •§ 8.5. Елементарні частинки та фундаментальні взаємодії
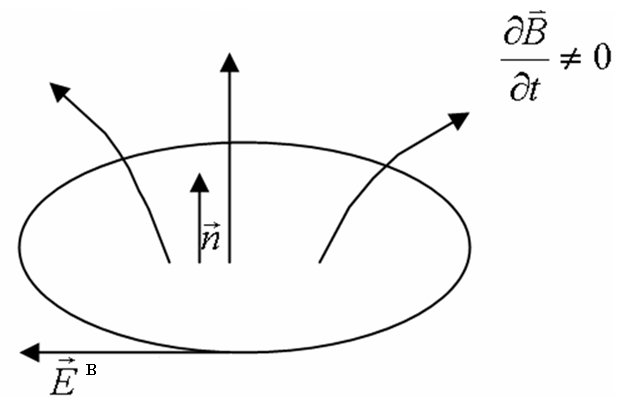
§ 4.11. Вихрове електричне поле
Розглянемо замкнений провідний контур, що перебуває в змінному магнітному полі (рис 4.23). Згідно з законом Фарадея (див. § 4.8), в цьому контурі індукується електрорушійна сила
![]() (4.53)
(4.53)
і
Рис.
4.23
![]() ,
на відміну від напруженості електростатичного
поля (створеного електричними зарядами),
яку будем надалі позначати
,
на відміну від напруженості електростатичного
поля (створеного електричними зарядами),
яку будем надалі позначати
![]() Тоді за означенням електрорушійної
сили:
Тоді за означенням електрорушійної
сили:
![]() . (4.54)
. (4.54)
З (4.53) і (4.54) одержимо
![]() .
.
Оскільки
контур нерухомий, то в останньому
рівнянні можна поміняти місцями операції
інтегрування та диференціювання. І
врахувавши, що в загальному
![]() ,
запишемо
,
запишемо
![]() (4.55)
(4.55)
На
відміну від електростатичного, поле
![]() ,
породжене змінним магнітним полем, є
вихровим, бо його циркуляція відмінна
від нуля
,
породжене змінним магнітним полем, є
вихровим, бо його циркуляція відмінна
від нуля
![]() ,
і тому силові лінії цього поля замкнені.
,
і тому силові лінії цього поля замкнені.
Якщо
ж у просторі одночасно існують і вихрове
(![]() ),
і електростатичне(
),
і електростатичне(![]() )
поля, то за принципом суперпозиції
напруженість результуючого поля
)
поля, то за принципом суперпозиції
напруженість результуючого поля
![]() +
+![]()
Як
було показано в розділі 3, ч.1, циркуляція
напруженості електростатичного поля
![]() Тому рівняння (4.55) можна узагальнити:
Тому рівняння (4.55) можна узагальнити:
![]() (4.56)
(4.56)
Ми отримали перше рівняння Максвелла: циркуляція вектора напруженості електричного поля дорівнює взятій з протилежним знаком швидкості зміни магнітного потоку через довільну поверхню, що опирається на контур циркуляції (рис. 4.23).
§ 4.12. Струми зміщення. Теорема про циркуляцію вектора напруженості магнітного поля (закон повного струму)
У
Рис.
4.24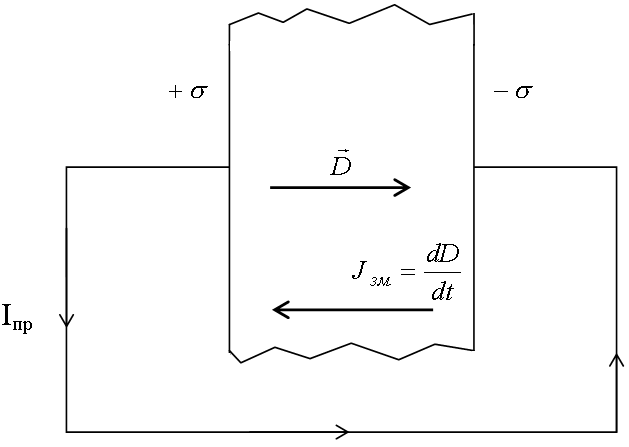
![]() ,
сполучити провідником (рис. 4.24), то по
провіднику потече електричний струм
(струм провідності)
,
сполучити провідником (рис. 4.24), то по
провіднику потече електричний струм
(струм провідності)
![]() ,
де S
– площа пластини конденсатора. Густина
струму провідності
,
де S
– площа пластини конденсатора. Густина
струму провідності
![]()
![]() . (4.57)
. (4.57)
Але
між обкладками конденсатора впорядкований
рух зарядів припиняється. Виникає
питання: чи зникає там і магнітне поле,
яке завжди пов’язане зі струмом? Гіпотеза
Максвелла (пізніше підтверджена
експериментально) полягає у тому, що
магнітне поле існує і між обкладками
конденсатора, оскільки там існує змінне
в часі електричне поле. Силовою
характеристикою електричного поля в
конденсаторі є вектор електричного
зміщення
![]() модуль якого, як показано в розділі 3
ч.1, дорівнює поверхневій густині вільних
зарядів на обкладках конденсатора:
модуль якого, як показано в розділі 3
ч.1, дорівнює поверхневій густині вільних
зарядів на обкладках конденсатора:
![]() .
Оскільки в процесі розрядки конденсатора
поверхнева густина заряду зменшується,
існує відмінне від нуля похідна
.
Оскільки в процесі розрядки конденсатора
поверхнева густина заряду зменшується,
існує відмінне від нуля похідна
![]() (4.58)
(4.58)
Цю
похідну Максвелл і назвав густиною
струму зміщення;
цей струм не пов'язаний з рухом зарядів
в просторі між обкладками конденсатора,
він існує незалежно від того, чи є в
конденсаторі діелектрик, чи там вакуум.
Потрібно лише, щоб існувало змінне
електричне поле, яке викликає струм
зміщення і породжене ним магнітне поле.
З (4.57) і (4.58) видно, що
![]() ,
тобто струм провідності в провіднику
неперервно переходить в струм зміщення
в діелектрику (або у вакуумі) (рис. 4.24).
,
тобто струм провідності в провіднику
неперервно переходить в струм зміщення
в діелектрику (або у вакуумі) (рис. 4.24).
Максвелл ввів також поняття повного струму, як суму струмів провідності та зміщення,
![]() .
(4.59)
.
(4.59)
В розімкненому електричному колі лінії повного струму завжди замкнені: в провідниках вони пов’язані з напрямленим рухом електричних зарядів, а в діелектриках (або вакуумі) – зі змінним електричним полем.
В § 4.3 була встановлена теорема про циркуляцію вектора напруженості магнітного поля струму провідності:
![]() . (4.60)
. (4.60)
По
теорії Максвелла, в правій частині
(4.60) повинна стояти сила повного струму.
Отже, після підстановки (4.59) в (4.60) одержимо
![]() .
Або, якщо виразити силу струму через
його густину, а також врахувати (4.58),
останній вираз можна записати у вигляді
.
Або, якщо виразити силу струму через
його густину, а також врахувати (4.58),
останній вираз можна записати у вигляді
![]() . (4.61)
. (4.61)
Рівняння (4.61) носить назву закону повного струму або 3-го рівняння Максвелла: циркуляція вектора напруженості магнітного поля дорівнює алгебраїчній сумі сил струмів провідності та струмів зміщення через поверхню S, обмежену контуром циркуляції.
