§ 5.6. Додавання взаємно перпендикулярних коливань

Нехай точка бере участь одночасно у двох взаємно перпендикулярних коливаннях однакової частоти:

(5.19)

, (5.20)

де А і В, α і β – відповідно амплітуди і початкові фази першого і другого коливань.

Встановимо рівняння траєкторії точки, виключивши із (5.19) і (5.20) час . Для цього перепишемо (5.19) і (5.20) у вигляді

, (5.21)

. (5.22)

Помноживши (5.21) на cos β і (5.22) на cos α та взявши різницю між отриманими рівняннями, одержимо

. (5.23)

Помноживши (5.21) на sin β і (5.22) на sin α та взявши їх різницю, одержимо

. (5.24)

Складаючи квадрати рівнянь (5.23) і (5.24), знайдемо рівняння траєкторії

. (5.25)

Рівняння (5.25) являє собою рівняння еліпса, характеристики якого визначаються значенням різниці початкових фаз (β – α).

Розглянемо частинні випадки:

1) Нехай де ; тоді а і рівняння (5.25) матиме вигляд

або .

Ми отримали рівняння прямої

яка проходить через початок координат і утворює з віссю ОХ кут, тангенс якого рівний . Таким чином, результуюче коливання залишається лінійним.

2) Нехай ; тоді . І траєкторією результуючого коливання буде еліпс, який описується рівнянням

. (5.26)

При А = В (5.26) переходить у коло. При проміжних значеннях (β – α) одержуються еліпси з різною орієнтацією своїх осей відносно осей координат.

Якщо взаємно перпендикулярні коливання відбуваються з різними частотами, то результуючі траєкторії мають більш складний вигляд; ці траєкторії називаються фігурами Ліссажу.

§ 5.7. Згасаючі коливання

Реальні коливання відбуваються в умовах дії сил тертя (опору). І тому реальні коливні системи є дисипативними, в яких механічна енергія частково втрачається, що призводить до поступового зменшення амплітуди, тобто до згасання коливань. Для спрощення обмежимось випадком лінійного коливання матеріальної точки у в’язкому середовищі. Якщо швидкість коливного руху невелика, то сила опору пропорційна до швидкості і напрямлена проти швидкості, тобто

,

де r – коефіцієнт опору.

Тоді за другим законом Ньютона

. (5.27)

Розділивши рівність (5.27) на m, отримаємо

. (5.28)

Введемо позначення

.

Рівняння (5.28) матиме вигляд диференціального рівняння згасаючих коливань:

. (5.29)

Підстановкою

(5.30)

приведемо рівняння (5.29) до простішого вигляду (тут е – основа натурального логарифму). Заміну змінних у (5.29) проведемо за допомогою рівнянь

(5.31)

Підставляючи (5.30) і (5.31) у (5.29), отримаємо

або

. (5.32)

У випадку, коли , можна ввести заміну Тоді рівняння (5.32) прийме вигляд

(5.33)

розв’язком якого є

. (5.34)

У випадку, коли , рух матеріальної точки буде неперіодичним (аперіодичним).

Підставляючи (5.34) у (5.30), одержимо рівняння руху коливної точки під дією квазіпружної сили та сили опору, тобто рівняння згасаючих коливань:

. (5.35)

З (5.35) видно, що амплітуда коливань зменшується з часом за експоненціальним законом (рис. 5.6):

Рис. 5.6

. (5.36)

Фізично β характеризує швидкість зменшення амплітуди і називається коефіцієнтом згасання. Можна показати, що β чисельно дорівнює оберненій величині часу релаксації τ, протягом якого амплітуда зменшується в е раз. Дійсно, якщо , то із (5.36) слідує, що

.

Звідси

.

Зручно користуватись поняттям логарифмічного декременту згасання λ, як натурального логарифму відношення двох послідовних амплітуд (через період Т):

.
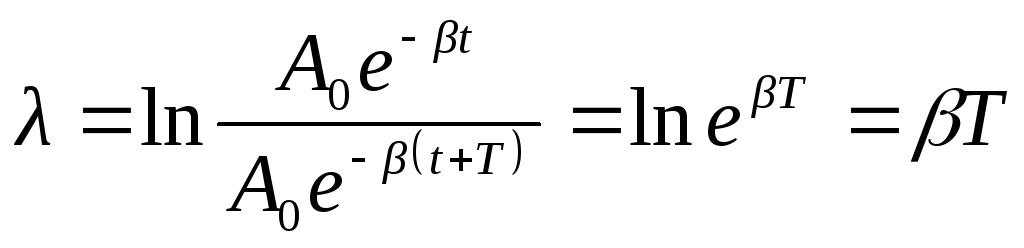