§ 7.14.2. Розподіл частинок з напівцілим спіном (ферміонів), в т.Ч. І електронів, за енергіями описується квантовою функцією розподілу Фермі-Дірака

, (7.91)

де f(E) – імовірність перебувати електрону на рівні з енергією Е, а F – енергія (рівень) Фермі. Зміст останньої зрозумілий з аналізу f(F) при Т = 0. Якщо Е > F, то f (Е) = 0, тобто рівень порожній; якщо Е < F, то f (F) =1, тобто рівень заповнений. Отже, енергія Фермі відповідає найвищому рівню, який ще заповнений при Т = 0 (рис. 7.30). При Т > 0 f(F) = 1/2, якщо Е=F, тобто енергія Фермі відповідає рівню, який при ненульовій температурі заповнений наполовину (рис. 7.30).

П

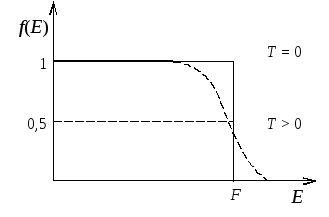Рис.7.30

ри певних умовах, а саме, коли Е - F >> k₀Т, квантовий розподіл Фермі-Дірака переходить в класичний розподіл Максвелла-Больцмана

. (7.92)

Електронний газ, що описується таким розподілом, називається невиродженим газом. В цей же час електронний газ, що описується розподілом Фермі-Дірака, називається виродженим. Критерієм виродження є нерівність

, (7.93)

тобто виродження має місце при високій концентрації електронів, малій їх ефективній масі та низьких температурах. В металах електронний газ завжди вироджений (n  10²² см^-3), в напівпровідниках, як правило, невироджений (n < 10¹⁸ см^-3).

В металах при низьких температурах концентрація електронів зони провідності, енергія яких лежить в інтервалі , складає

де dg(E) – кількість енергетичних рівнів у вказаному інтервалі. Якщо справедливий параболічний закон дисперсії (7.90), то нескладний розрахунок дає

.

Тоді повна концентрація носіїв в с-зоні металу при низьких температурах

(7.94)

і від температури не залежить. Енергія Фермі

,

що дає при . Середня енергія зонних електронів в металах 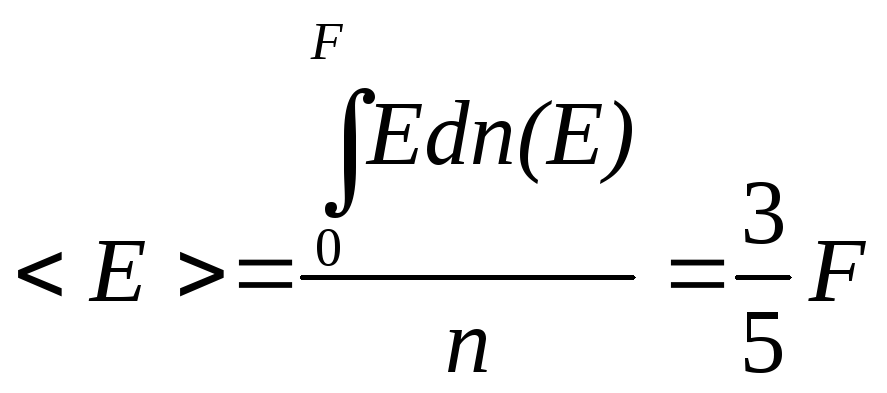, що значно більше від k₀Т.

А це означає, що лише незначна кількість електронів, що перебувають на рівнях, близьких до рівня Фермі, може змінити свою енергію при зміні температури. Таким чином, електронний газ в металах практично не вносить вкладу в теплоємність кристалу (див. § 7.13), незважаючи на високу загальну концентрацію електронів.

В напівпровідниках рівень Фермі, як правило, лежить в забороненій зоні (рис.7.29), і тому при розрахунку концентрації невироджених електронів в зоні провідності потрібно врахувати, що функція розподілу (7.92) в усьому діапазоні енергій Е > E_c менша від одиниці і залежить від температури. І тому

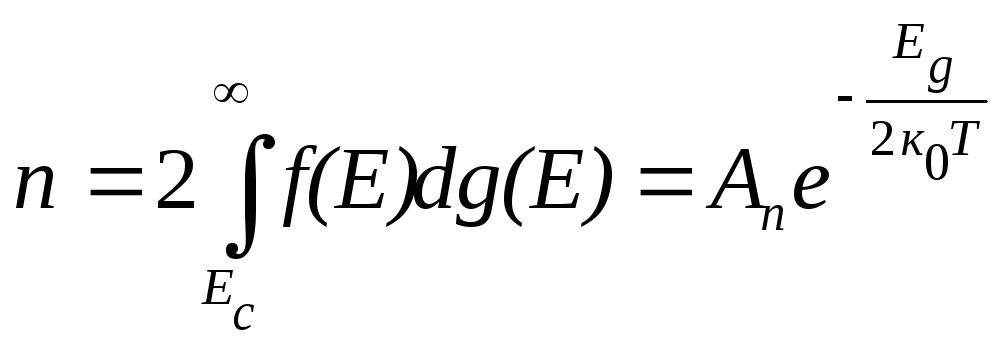, (7.95)

де А_n – множник, який слабо залежить від температури і визначається ефективною масою носіїв, а Е_g – ширина забороненої зони.

Як слідує з (7.95), з ростом температури концентрація зонних (вільних) електронів збільшується за експоненційним законом. Ця формула справедлива лише для бездомішкового, т.з. власного, напівпровідника. Зрозуміло (див. рис. 7.29), що концентрація дірок у валентній зоні дорівнює концентрації електронів в зоні провідності: n = p = n_i – власна концентрація носіїв струму.

С

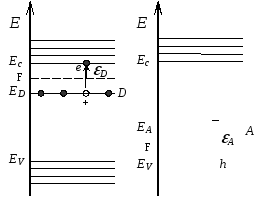Рис.7.31

итуація радикально змінюється, коли в напівпровідник ввести домішки. Зокрема, коли вводяться донорні домішки, тобто домішки, які легко віддають електрони в С-зону, то n >> p; такий домішковий напівпровідник називається електронним (n-типу). Якщо ж вводяться акцепторні домішки, тобто домішки, які легко захоплюють електрони з V-зони, то p >> n; такий домішковий напівпровідник називається дірковим (р-типу). В класичних напівпровідниках Ge i Si в ролі донорних домішок виступають As, P, а акцепторних – Ga, Іn.

Оскільки енергія іонізації донорів та акцепторів значно менша від ширини забороненої зони, то енергетичні рівні цих домішок розміщені в забороненій зоні на відстані енергії іонізації (_Д, _А) від дна зони провідності чи вершини валентної зони, відповідно (рис. 7.31). При низьких температурах, коли іонізація домішок є слабкою, а власна генерація носіїв – несуттєва, концентрація носіїв в зонах запишеться:

для n-типу: , (7.96)

для p-типу: , (7.97)

де B_n і B_p – множники, які слабо залежать від температури, а визначаються концентрацією відповідних домішок і ефективною масою носіїв струму. Отже, і в цьому випадку концентрація носіїв збільшується експонеційно з ростом температури кристалу. Відмітимо, що рівень Фермі в домішкових напівпровідниках розміщений біля країв відповідних зон (рис. 7.31).