§ 7.8. Принцип Паулі. Стани електронів в складних атомах

7.8.1. Отже, електрони в атомі описуються четвіркою квантових чисел: головне квантове число n, орбітальне квантове число , магнітне квантове число m_l і магнітне спінове квантове число m_s. У воднеподібних атомів енергія електрона залежить лише від головного квантового числа. В складних, багатоелектронних атомах окремий електрон перебуває в полі не тільки ядра, але і решти електронів. Це призводить до зняття виродження по , і енергія електрона залежить як від n, так і від . При цьому, як правило, залежність від n сильніша.

Якщо багатоелектронний атом перебуває в незбудженому стані, то його електрони намагатимуться зайняти стани з мінімальною енергією (стан стійкої рівноваги). Таким є стан 1s (n = 1;  = 0). Але реалізувати таку ситуацію забороняє принцип Паулі (1925 р.), справедливий лише для ферміонів: в системі тотожних ферміонів в певному стані може перебувати лише одна частинка. Оскільки електрони є ферміонами, то цей принцип стосовно електронів в атомі формулюється наступним чином: лише один електрон в атомі може володіти тотожним набором чотирьох квантових чисел: . А це означає, що в стані 1s може перебувати лише два електрони з протилежними спінами (), решта електронів повинна перебувати в інших станах. Для опису розподілу Z електронів незбудженого багатоелектронного атома по станах введемо поняття шарів і оболонок.

До шару належать електрони, які мають однакове головне квантове число n. Максимальна кількість електронів в шарі – 2n². Шари класифікуються як: К(n = 1), L(n = 2), M(n = 3), N(n = 4) тощо. До оболонки належать електрони, які мають однакові квантові числа n і . Максимальна кількість електронів в оболонці – 2(2+1). Оболонки класифікуються як: 1s(n = 1, = 0), 2s(n = 2, = 0), 2p(n = 2, = 1) тощо. Електронна конфігурація, наприклад, атома міді, який має 29 електронів, представлена наступним чином:

1s² 2s² 2p⁶ 3s² 3p⁶ 3d¹⁰ 4s¹.

Тут цифри над символами оболонок вказують на кількість електронів в них. Видно, що К-шар вміщує лише одну оболонку, інші шари мають по декілька оболонок.

6.8.2. Взаємодія між електронами складних атомів зумовлена як чисто електростатичними силами, так і магнітними силами, оскільки кожен електрон володіє як орбітальним, так і спіновим магнітним моментом. Остання взаємодія називається спін-орбітальною.

Якщо електростатична взаємодія сильніша від спін-орбітальної, то реалізується зв’язок Рассель-Саундерса, при якому спочатку сумуються окремо орбітальні, окремо спінові моменти всіх електронів атома (оболонки, шару), тобто

.

А сумарний (повний) момент електронів атома (оболонки, шару) шукається як векторна сума орбітального і спінового моментів, тобто

.

Квадрат цих векторів виражається через відповідні квантові числа L, S, J наступними співвідношеннями:

(7.60)

де L – орбітальне квантове число атома (оболонки, шару), яке приймає цілочисельні значення між максимальним і мінімальним значенням алгебраїчної суми , S – спінове квантове число атома (оболонки, шару), яке приймає значення між максимальним і мінімальним значенням алгебраїчної суми , J – внутрішнє квантове число атома (оболонки, шару), яке може приймати значення від до L + S. Наприклад, для частково заповненої оболонки np² вказані квантові числа можуть приймати значення: L = 0, 1, 2; S = 0, 1; J = 0, 1, 2. Відмітимо, що одночасно не може реалізуватися ситуація, в якій L = 2 i S = 1, (а, отже, J = 3), бо при цьому порушиться принцип Паулі.

Стани з різними можливими значеннями квантових чисел L, S, J називаються термами, які позначаються символічно як ^2S+1L_J, де замість числового значення L пишуть відповідну велику букву S(L = 0), P(L = 1), D(L = 2) тощо. Для наведеного прикладу можливими є наступні терми: ¹S₀, ³S₁, ¹P₁, ³P₀, ³P₁, ³P₂, ¹D₂. Зрозуміло, що основний стан оболонки, тобто стан з мінімальною енергією, реалізується через один з наведених термів (в даному випадку таким є терм ³P₀). Усі інші терми характеризують збуджені стани.

Зв’язок Рассель-Саундерса реалізується в більшості атомів. Але для деяких великих атомів спін-орбітальна взаємодія сильніша від електростатичної. В цьому випадку реалізується зв’язок (jj), при якому спочатку додаються векторно орбітальний і спіновий моменти окремих електронів, утворюючи повний момент і-го електрона

а сумарний повний момент атома (оболонки, шару) визначається як векторна сума повних моментів окремих електронів:

(7.61)

де J – знову ж внутрішнє квантове число атома (оболонки, шару).

Розрахунок згадуваних моментів атомів полегшується тим, що для повністю заповненої оболонки ці моменти дорівнюють нулю. Проілюструємо це для p-оболонки атома зі зв’язком Рассель-Саундерса, використавши сумування проекцій моментів на вісь z, тобто використовуючи квантові числа і усіх електронів p-оболонки, з урахуванням принципу Паулі. Дійсно:

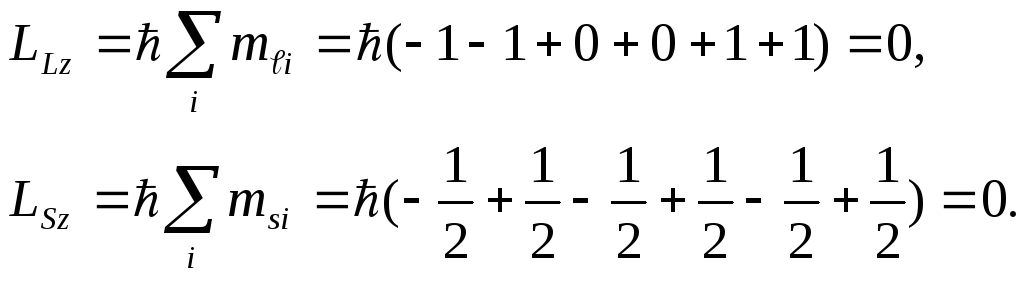
В такому разі стан атома визначається електронами частково заповнених оболонок. В більшості атомів внутрішні оболонки (1s, 2s, 2p, …) заповнені повністю, а частково заповнена лише зовнішня оболонка (хоч і є винятки). Електрони зовнішніх оболонок найслабше зв’язані зі своїм ядром і тому забезпечують зв’язок між атомами в молекулах і в кристалічних гратках твердих тіл. Такі електрони називаються валентними, вони відповідальні за спектри випромінювання і поглинення атомів.