§ 7.5. Квантовий лінійний гармонічний осцилятор

7.5.1. Лінійний гармонічний осцилятор – це матеріальна точка, яка здійснює одновимірний (вздовж осі х) рух під дією квазіпружної сили . Потенціальна енергія осцилятора (рис. 7.8)

, (7.41)

де m – маса осцилятора, – його власна циклічна частота, х – зміщення від положення рівноваги. Отже, мова піде про мікрочастинку, яка перебуває в потенціальній ямі з параболічними стінками. Підставляючи (7.41) в рівняння Шредінгера (7.30), отримаємо

. (7.42)

Власні хвильові функції, тобто розв’язки цього рівняння, які задовольняють стандартні вимоги (§ 7.3), мають вигляд

, (7.43)

д

Рис. 7.8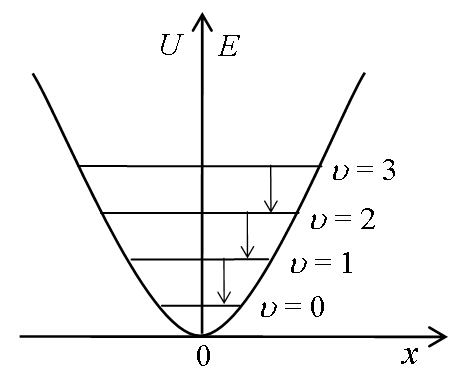

е , – поліноми Чебишева-Ерміта -го порядку, – коливальне квантове число.

Для класичного осцилятора зміщення х обмежене амплітудою коливань ; для квантового осцилятора таке обмеження знімається за рахунок можливості тунелювати через стінки потенціальної ями. А це означає, що існує ненульова імовірність знайти мікрочастинку поза ямою.

Власні значення оператора Гамільтона для квантового осцилятора

. (7.44)

Тут враховано, що . Отже, енергія квантового осцилятора приймає дискретні значення , тобто квантується (рис. 7.8). Найменша енергія квантового осцилятора, так звана нульова енергія, на відміну від класичного осцилятора, не дорівнює нулю. Наявність нульових коливань підтверджується експериментально в дослідах по розсіюванню світла в кристалах при дуже низьких температурах, коли з точки зору класичної фізики коливальний рух кристалічної гратки повинен би припинитися.

Перебуваючи в стаціонарному стані, квантовий осцилятор не поглинає і не випромінює енергії. Випромінювання (поглинання) світла відбувається при переході осцилятора між стаціонарними станами, при цьому квантова механіка дозволяє лише переходи між сусідніми енергетичними рівнями, тобто (правило відбору). Енергія випромінюваного (поглинутого) кванту , що підтверджує квантовий постулат Планка.

§ 7.6. Воднеподібні атоми в квантовій механіці. Квантові числа

7.6.1. З врахуванням виразу (7.3) для потенціальної енергії електрона в кулонівському полі ядра воднеподібного атома, стаціонарне рівняння Шредінгера набуде вигляду

. (7.45)

О

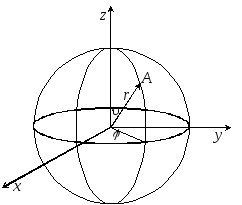Рис. 7.9

скільки кулонівське поле володіє центральною симетрією, то зручно перейти до сферичних координат (рис. 7.9), де положення довільної точки А описується трьома координатами . В цьому випадку рівняння Шредінгера набуває вигляду, складнішого від (7.45), але з’являється можливість представити хвильову функцію як добуток радіальної функції R(r) і кутової , тобто провести розділення змінних:

. (7.46)

Стандартні вимоги як до хвильової функції в цілому, так і до окремих складових забезпечуються лише при певних, дискретних значеннях не тільки енергії електрона, але і квадрату моменту імпульсу його орбітального руху , а також проекції цього моменту на вибраний напрямок (вісь z). Квантування вказаних характеристик визначається трьома квантовими числами: головним n, орбітальним (азімутальним) та магнітним наступним чином:

, (7.47)

де n=1,2,3,…, тобто співпадає з (7.8) для борівського воднеподібного атома;

, (7.48)

де = 0,1,2,…, (n-1);

, (7.49)

де .

М

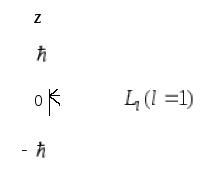Рис.7.10

агнітне квантове число вказує на просторове квантування моменту імпульсу електрона: вектор моменту імпульсу електрона може мати лише такі орієнтації в просторі, що його проекції на вибрану вісь z (яка задається, як правило, напрямком магнітного поля) кратні (рис. 7.10).

Оскільки енергія електрона Е_n визначається лише головним квантовим числом n, а хвильова функція – усіма квантовими числами, то декільком станам з різними та відповідає одне значення енергії. Така ситуація називається квантовомеханічним виродженням. Наприклад, енергія Е₂ реалізується в чотирьох станах з хвильовими функціями . В загальному, кратність виродження дорівнює n². Для ілюстрації приведемо вирази для радіальних і кутових функцій в декількох станах:

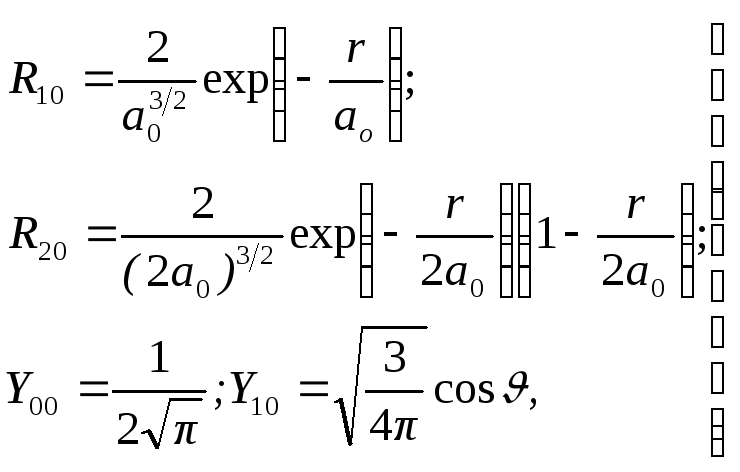(7.50)

де – борівський радіус.

Для основного стану (n = 1) хвильова функція має вигляд

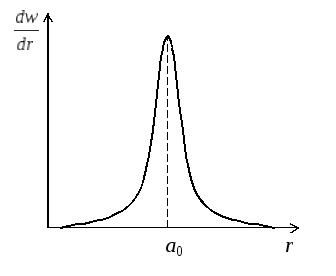Рис.7.11

. (7.51)

Імовірність знайти електрон в сферичному шарі товщиною dr, тобто в елементарному об’ємі , становить

а в шарі одиничної товщини –

. (7.52)

Як видно з рис. 7.11, залежність володіє різким максимумом при r = а₀. Отже, борівська орбіта в квантовій механіці може інтерпретуватись як геометричне місце точок, де імовірність перебування електрона – максимальна. Але, оскільки заряд електрона “розмазаний” по усьому атомі , то в квантовій механіці, у відповідності зі співвідношенням невизначеностей Гейзенберга, поняття орбіти (траєкторії) електрона втрачає зміст.

7.6.2. Стани електрона з різними значеннями орбітального квантового числа прийнято позначати наступним чином:

	0	1	2	3	4	.
Стан	s	p	d	f	g

І

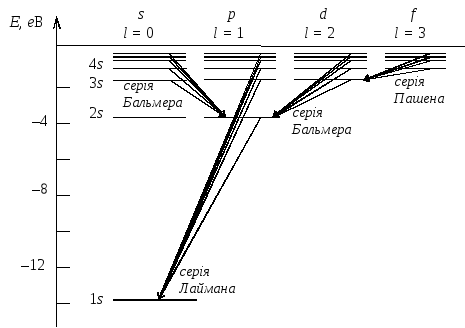Рис.7.12

тому енергетичні рівні з різними n реалізуються наступними станами:

n = 1 –	стан	1s;
n = 2 –	стани	2s,	2p;
n = 3 –	стани	3s,	3p,	3d;
n = 4 –	стани	4s,	4p,	4d,	4f.

Стан 1 s є основним, усі інші стани – збуджені. Час життя електрона в збудженому стані складає ~.

Енергетична діаграма квантовомеханічного атома водню має вигляд (рис. 7.12), який дещо відрізняється від діаграми борівського атома (рис. 7.4). Як і раніше, квантова механіка не накладає жодного обмеження на зміну головного квантового числа. В цей же час зміна і регламентується правилами відбору

. (7.53)

Друге правило відбору тут не проявляється, але стає важливим, коли випромінюючі атоми перебувають в магнітному полі.