§ 4.4. Дія магнітного поля на струм; сила Ампера. Магнітна взаємодія струмів

Як відмічалося вище, магнітне поле діє на вміщений у нього провідник зі струмом. Французький фізик Ампер встановив, що на елемент провідника зі струмом , вміщений в магнітне поле індукцією , діє сила (сила Ампера)

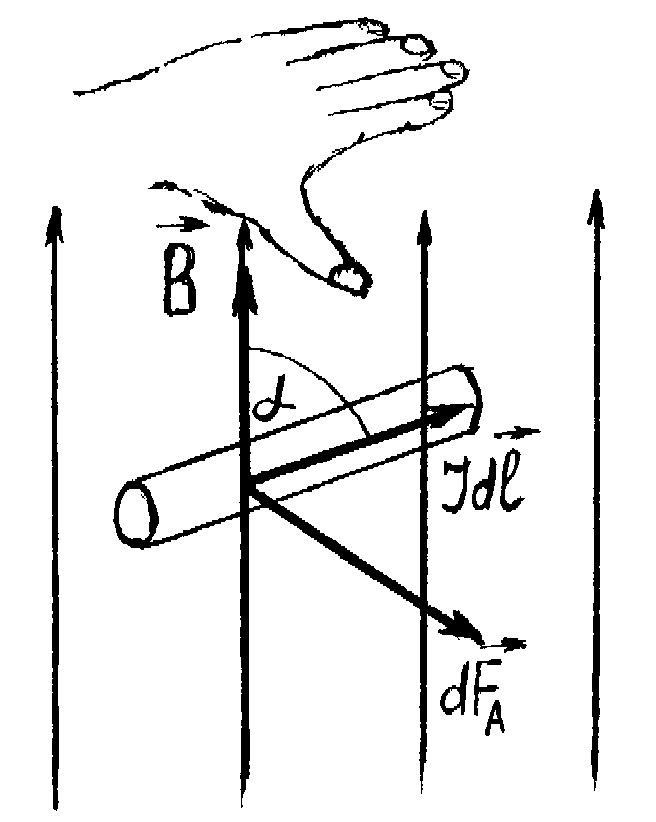Рис. 4.12

(4.22)

або в скалярній формі

, (4.23)

де α – кут між напрямками струму та магнітної індукції. Напрямок сили Ампера можна визначити за правилом лівої руки (рис. 4.12).

Сила, що діє на провідник зі струмом скінченої довжини, знаходиться з (4.22) або (4.23) інтегруванням по всій довжині провідника:

(4.24)

Зокрема, для прямолінійного провідника довжиною в однорідному магнітному полі

. (4.25)

Розглянемо тепер взаємодію двох довгих прямолінійних провідників, паралельних один одному і по яких протікають струми однакового напрямку. Ділянки таких провідників зображені на рис. 4.13.

Сила, з якою магнітне поле першого струму діє на ділянку другого провідника довжиною , згідно з (4.25)

.

Згідно з (4.13)

Рис. 4.13

(d – відстань між провідниками).

Як видно з рис. 4.13, кут α між напрямком струму в другому провіднику і вектором магнітної індукції поля першого провідника – прямий; отже, .

Тоді одержимо

. (4.26)

Це і є вираз для сили взаємодії провідників зі струмом (адже так само можна отримати і вираз для сили F_2,1). Напрямки сил знайдені за правилом лівої руки і вказані на рис. 4.13. Отже, струми однакового напрямку притягуються. Аналогічно, можна показати, що антипаралельні струми будуть відштовхуватись.

Із формули (4.26), вважаючи в ній всі величини одиничними (за винятком ), отримаємо визначення одиниці сили струму: Ампер – це сила такого постійного струму, який при проходженні по двох прямолінійних паралельних нескінченно довгих провідниках, розміщених на відстані 1 м у вакуумі, викликає між ними магнітну взаємодію силою на кожен метр довжини. Це визначення використовувалось в СІ до 90-их років минулого століття.

§ 4.5. Сила Лоренца. Рух електричних зарядів в магнітному полі

Досліди показують, що на електричний заряд, який рухається в магнітному полі, діє з боку поля сила (сила Лоренца), що напрямлена перпендикулярно до швидкості і пропорційна величині заряду і векторному добутку його швидкості та магнітної індукції:

(4.27)

або в скалярній формі

, (4.28)

де α – кут між .

Д

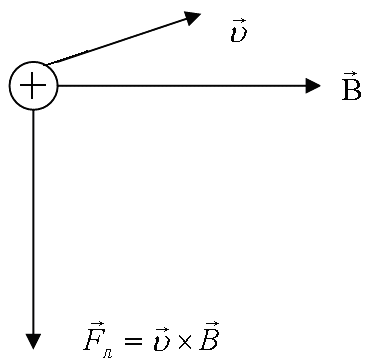Рис. 4.14

ля додатнього заряду напрямок сили Лоренца визначається за правилом лівої руки (рис. 4.14), а для від’ємного заряду цей напрямок протилежний (рис. 4.15).

Окремо відмітимо, що на нерухомий заряд магнітне поле не діє; в цьому його принципова відмінність від електростатичного поля. Якщо ж на заряд q діють одночасно і електричне, і магнітне поле, то результуюча сила (що також називається силою Лоренца)

, (4.29)

де – напруженість електростатичного поля. Очевидно, що (4.27) є окремим випадком (4.29) у разі, коли електростатичне поле відсутнє.

Я

Рис. 4.15

кщо заряджена частинка рухається вздовж ліній магнітної індукції (або у протилежному напрямку), то або . Згідно з (4.28) у цьому випадку магнітне поле на частинку не діє, і вона рухається рівномірно і прямолінійно. Якщо ж швидкість частинки , то F_Л – максимальна. Оскільки перпендикулярна до швидкості, то вона надає частинці нормального прискорення; отже, частинка буде рухатися по колу в площині, перпендикулярній до напрямку магнітного поля. Згідно з 2-м законом Ньютона

,

звідки радіус кола

, (4.30)

а період обертання

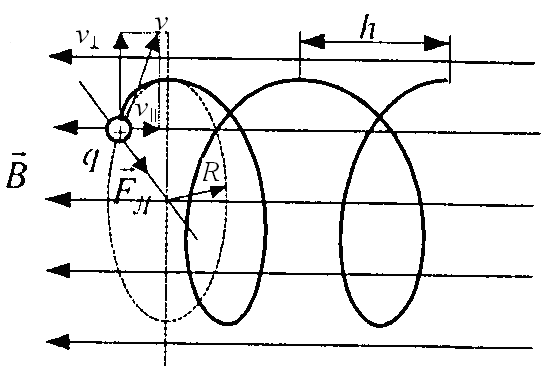Рис. 4.16

. (4.31)

Якщо ж швидкість частинки складає довільний кут α з напрямком магнітної індукції , то її рух можна розглядати (рис. 4.16) як суперпозицію рівномірного прямолінійного руху вздовж поля зі швидкістю і рівномірного руху по колу радіуса в площині, перпендикулярній до поля. Результатом суперпозиції буде рух по спіралі (рис. 4.16). Крок спіралі

. (4.32)

Напрямок, в якому закручується спіраль, залежить від знаку заряду частинки.

З попереднього розгляду видно, що сила Лоренца при русі заряду в магнітному полі роботи не виконує; вона перпендикулярна до швидкості, отже змінює лише напрямок швидкості, не змінюючи її модуля.