§ 7.4. Частинка в одновимірній прямокутній потенціальній ямі. Проходження частинки через потенціальний бар’єр

7

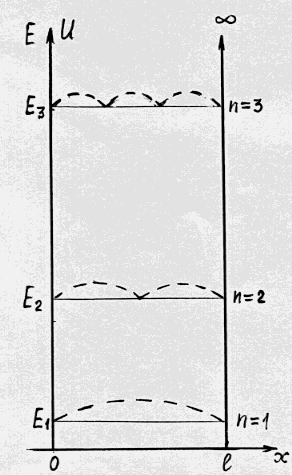Рис.7.6

.4.1. Усякий зв’язаний стан частинки (вільний електрон в металі, нуклон в ядрі тощо), тобто стан з від’ємною потенціальною енергією, можна описати, ввівши поняття потенціальної ями. Розглянемо найпростіший випадок, коли частинка масою m перебуває в одновимірній прямокутній нескінченно глибокій потенціальній ямі шириною l. Оскільки початок відліку потенціальної енергії можна вибирати довільно, то задачу про “яму” замінимо задачею про “ящик”, на дні якого потенціальна енергія дорівнює нулю, а стінки якого нескінченно високі (рис. 7.6). Оператор Гамільтона (7.26) для цього випадку має вигляд

,

де

Всередині ящика рівняння Шредінгера (7.30) запишеться як

або

. (7.32)

Введемо позначення

, (7.33)

де k має зміст хвильового числа, якщо врахувати (7.31). Тоді (7.32) набуде форми, подібної (формально) до диференціального рівняння власних гармонічних коливань,

.

Розв’язок цього рівняння шукаємо у вигляді гармонічної функції координати х:

. (7.34)

Оскільки хвильова функція повинна бути неперервною, в тому числі і на стінках ями, а вийти за межі ями частинка не може, то . Перша гранична умова дає , і тому

. (7.35)

Друга гранична умова дає

, (7.36)

де n = 1, 2, 3, … – квантове число стану частинки.

Врахувавши, що , отримаємо з (7.36) співвідношення , тобто в межах ширини ями повинно вкладатись ціле число півхвиль де Бройля.

Формальну амплітуду А в (7.35) знайдено з умови нормування хвильової функції до одиниці:

.

Звідси , і остаточно хвильова функція частинки в довільному квантовому стані n, з врахуванням (7.36), набуває вигляду

. (7.37)

Об’єднуючи (7.33) і (7.36), отримаємо вираз для енергії частинки в різних квантових станах

. (7.38)

Отже, енергія частинки в потенціальній ямі приймає не довільні, а дискретні значення Е₁, Е₂, Е₃, …, зображені на рис. 7.6 відповідними енергетичними рівнями. Густина імовірності (на рисунку – штрихові лінії) залежить від координати частинки, при цьому по різному в кожному квантовому стані. Наприклад, для центру ями вона максимальна в стані n = 1 і дорівнює нулю в стані n = 2.

Відстань між сусідніми енергетичними рівнями

. (7.39)

Р

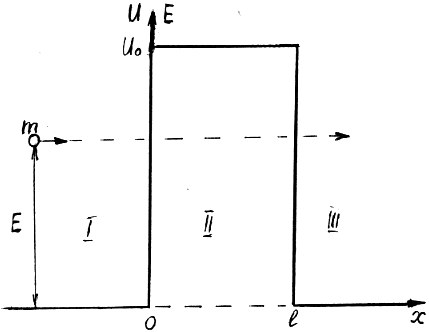Рис. 7.7

озглядаючи електрон в атомі як такий, що перебуває в потенціальній ямі шириною , отримаємо , що співмірно з енергією електрона. В цей же час в макросвіті, коли m i l – дуже великі, відстань між енергетичними рівнями стає зникаюче малою, і квантуванням енергії можна знехтувати.

Задача про частинку в потенціальній ямі скінченної глибини розв’язується значно складніше, але висновок про квантування енергії і в цьому випадку залишається в силі.

7.4.2. Спорідненою до описаної є задача про проходження частинки через потенціальний бар’єр. Нехай мікрочастинка з масою m і енергією Е налітає на одновимірний прямокутний потенціальний бар’єр шириною l і висотою U₀ (рис. 7.7). Якщо частинка класична, то вона пролітає над бар’єром, коли Е > U₀, і відбивається від нього, коли Е < U₀. Проникнути під бар’єр класична частинка не може, бо тоді її кінетична енергія була б меншою від нуля. Розв’язок рівняння Шредінгера для квантомеханічної мікрочастинки дає, що хвильові функції в усіх трьох областях відмінні від нуля, тобто мікрочастинка проникає під бар’єр і за бар’єр. Це явище називається тунелюванням. Від’ємні значення кінетичної енергії мікрочастинки в момент проходження бар’єру не можуть турбувати, бо в квантовій механіці кінетична енергія , як і потенціальна енергія, не є точно визначеними. Прозорість бар’єру, тобто імовірність тунелювання частинки, знаходиться як відношення густин імовірності в областях ІІІ та І. Розрахунок дає

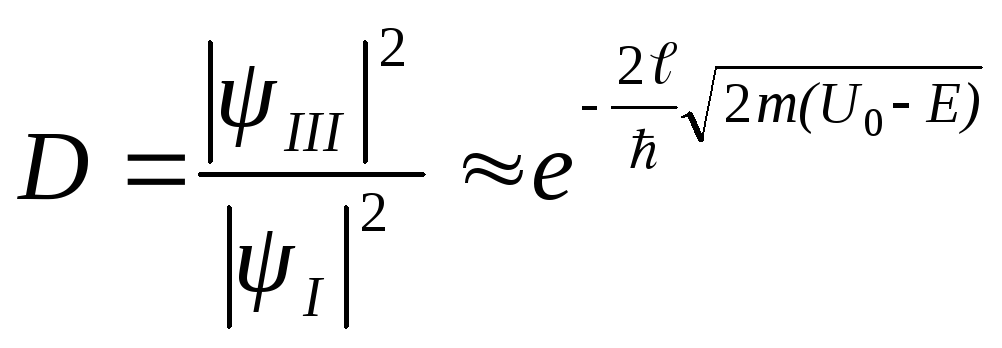. (7.40)

Звідси видно , що бар’єр тим прозоріший, чим менші його ширина і висота. Для класичної частинки (m  ) і макробар’єру (l  ) прозорість бар’єру зникаюче мала.